ACME Example: Difference between revisions
Chris Kahn (talk | contribs) |
Kate Racaza (talk | contribs) No edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner ALTA Examples}}</noinclude> | |||
ACME manufacturing has implemented an accelerated testing program for their new design. A total of 40 units were tested at four different pressure levels. The operating stress level is 170 psi. | ACME manufacturing has implemented an accelerated life testing program for their new product design. A total of 40 units were tested at four different pressure levels. The operating stress level is 170 psi. The following table shows the data from the test. Determine the parameters of the inverse power law Weibull model and obtain the use level probability plot with 90% 2-sided confidence bounds on time. | ||
{| | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | ||
|- | |- | ||
!Stress Level, psi | !Stress Level, psi | ||
| Line 32: | Line 32: | ||
|} | |} | ||
The parameters of the IPL-Weibull model are estimated to be: | |||
| Line 62: | Line 48: | ||
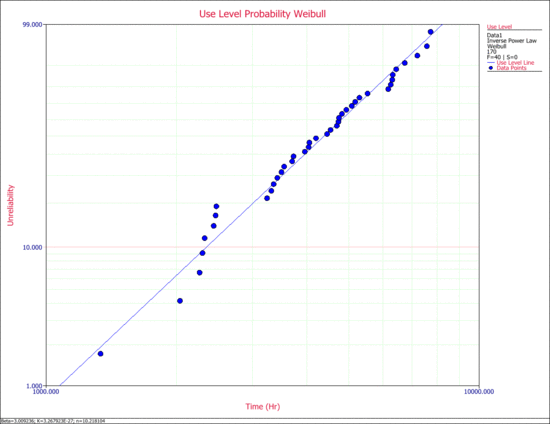
The use level probability plot is shown next. | |||
[[Image:new_7.gif | [[Image:new_7.gif|center|550px|The probability plot at a use stress level.]] | ||
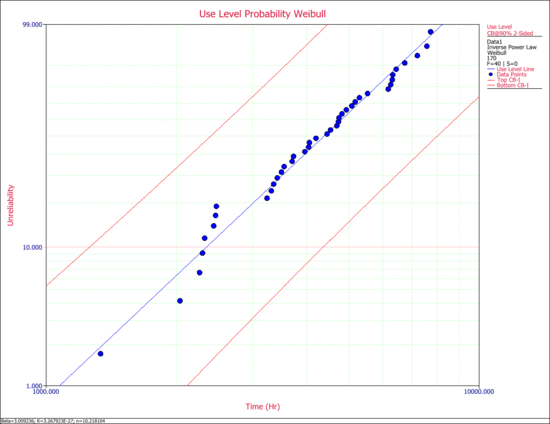
In ALTA, the confidence bounds on time are the Type 1 bounds (Time Bounds). | |||
[[Image:new_9.gif|center|550px|The probability plot at a use stress level with 90% Type I confidence bounds.]] | |||
Latest revision as of 04:08, 15 August 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.
ACME manufacturing has implemented an accelerated life testing program for their new product design. A total of 40 units were tested at four different pressure levels. The operating stress level is 170 psi. The following table shows the data from the test. Determine the parameters of the inverse power law Weibull model and obtain the use level probability plot with 90% 2-sided confidence bounds on time.
| Stress Level, psi | 220 psi | 230 psi | 240 psi | 250 psi |
|---|---|---|---|---|
| 165 | 93 | 72 | 26 | |
| 177 | 106 | 73 | 44 | |
| 238 | 156 | 99 | 63 | |
| 290 | 170 | 124 | 68 | |
| Times-to-failure, hr | 320 | 185 | 134 | 69 |
| 340 | 214 | 150 | 72 | |
| 341 | 220 | 182 | 77 | |
| 380 | 236 | 186 | 96 | |
| 449 | 252 | 190 | 131 | |
| 544 | 288 | 228 | 140 |
The parameters of the IPL-Weibull model are estimated to be:
- [math]\displaystyle{ \begin{align} \beta =\ & 3.009236 \\ K=\ & 3.267923E-27 \\ n=\ & 10.218104 \end{align} }[/math]
The use level probability plot is shown next.
In ALTA, the confidence bounds on time are the Type 1 bounds (Time Bounds).