Interval Data Example: Difference between revisions
Chris Kahn (talk | contribs) |
Kate Racaza (talk | contribs) No edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner ALTA Examples}}</noinclude> | |||
100 units of an electronic device are tested using two test chambers. Each test chamber contains 50 units and is set to a different temperature. The test is performed continuously for 15 weeks, but monitored only on a weekly basis; therefore, the exact times at which the units failed are unknown. For each failed unit, the only information available is whether or not it failed between inspections. | |||
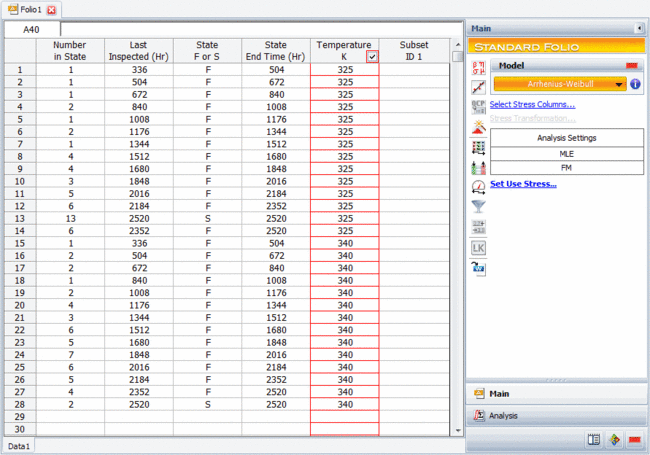
The goal of the test is to estimate the 90% lower bound on the <math>B10</math> life (in hours) of the electronic device. The data obtained from the test are recorded in an ALTA standard folio, using the interval data format, as shown next. The normal use condition is assumed to be 300K. | |||
Assuming that the failure times of the | |||
[[Image:chapter14_80.gif|center|650px|]] | |||
Assuming that the failure times of the device follow a Weibull distribution and that the Arrhenius model is an adequate life-stress relationship, we obtain the following estimates for the parameters: | |||
| Line 17: | Line 19: | ||
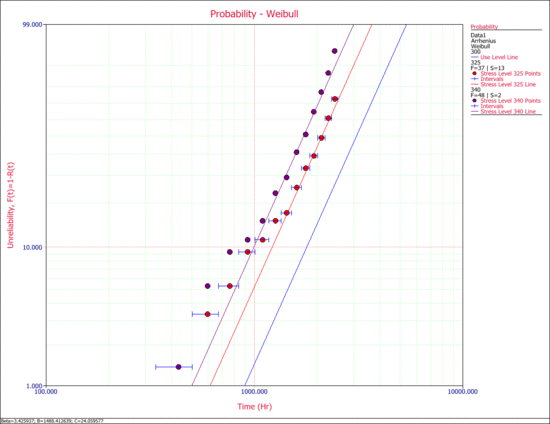
The next figure show the probability lines at the different stress levels along with the extrapolated use level probability line. | The next figure show the probability lines at the different stress levels, along with the extrapolated use level probability line. | ||
[[Image:intervaldataproblines.gif|center|550px|Probability lines at the different test stress levels with the extrapolated use level probability line.]] | |||
[[Image:intervaldataproblines.gif | |||
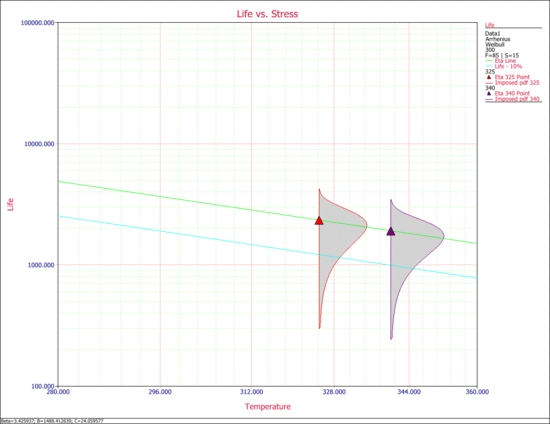
The following Life vs. Stress plot shows the <math>B10</math> life line. | |||
The following | |||
[[Image:ch14-23.gif|center|550px|Life vs. Stress with the ''B''10 life line (bottom).]] | |||
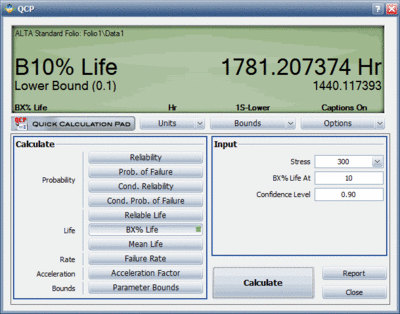
The 90% lower bound on the <math>B10</math> life can be estimated as follows. | The 90% lower bound on the <math>B10</math> life can be estimated as follows. | ||
[[Image:intervalb10qcp.gif|center|400px|]] | |||
[[Image:intervalb10qcp.gif | |||
Latest revision as of 01:54, 15 August 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.
100 units of an electronic device are tested using two test chambers. Each test chamber contains 50 units and is set to a different temperature. The test is performed continuously for 15 weeks, but monitored only on a weekly basis; therefore, the exact times at which the units failed are unknown. For each failed unit, the only information available is whether or not it failed between inspections.
The goal of the test is to estimate the 90% lower bound on the [math]\displaystyle{ B10 }[/math] life (in hours) of the electronic device. The data obtained from the test are recorded in an ALTA standard folio, using the interval data format, as shown next. The normal use condition is assumed to be 300K.
Assuming that the failure times of the device follow a Weibull distribution and that the Arrhenius model is an adequate life-stress relationship, we obtain the following estimates for the parameters:
- [math]\displaystyle{ \begin{align} \beta =\ & 3.425937 \\ B=\ & 1488.412639 \\ C=\ & 24.059577 \end{align} }[/math]
The next figure show the probability lines at the different stress levels, along with the extrapolated use level probability line.
The following Life vs. Stress plot shows the [math]\displaystyle{ B10 }[/math] life line.
The 90% lower bound on the [math]\displaystyle{ B10 }[/math] life can be estimated as follows.