Arrhenius Example: Difference between revisions
m (moved Arrhenius-Weibull Example to Arrhenius Example) |
Lisa Hacker (talk | contribs) No edit summary |
||
| (11 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
{ | <noinclude>{{Banner ALTA Examples}} | ||
''This example appears in the [https://help.reliasoft.com/reference/accelerated_life_testing_data_analysis Accelerated life testing reference].'' | |||
</noinclude> | |||
< | |||
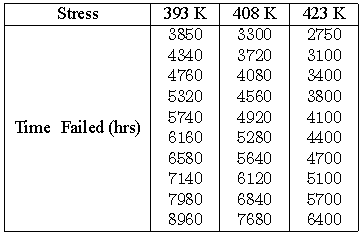
Consider the following times-to-failure data at three different stress levels. | Consider the following times-to-failure data at three different stress levels. | ||
[[Image:6stresstimefailed.gif|center|400px|]] | |||
[[Image:6stresstimefailed.gif | |||
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields: | The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields: | ||
::<math>\widehat{\beta }=4.2915822</math> | ::<math>\widehat{\beta }=4.2915822\,\!</math> | ||
::<math>\widehat{B}=1861.6186657\,\!</math> | |||
::<math>\widehat{B}=1861.6186657</math> | |||
::<math>\widehat{C}=58.9848692\,\!</math> | |||
::<math>\widehat{C}=58.9848692</math> | |||
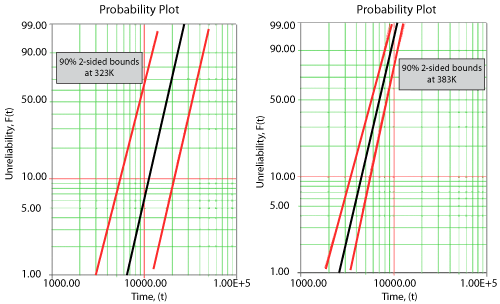
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in [[Appendix A: Brief Statistical Background|Appendix A]]. Specific calculations for confidence bounds on the Arrhenius model are presented in the [[Arrhenius_Relationship#Arrhenius_Confidence_Bounds|Arrhenius Relationship chapter]]). | |||
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure the more distant the accelerated stress from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in [[Appendix A: Brief Statistical Background|Appendix A]]. Specific calculations for confidence bounds on the Arrhenius model are presented in [[Arrhenius Relationship | |||
[[ | [[Image:ALTA6_10_new.png|center|800px|Comparison of the confidence bounds for different use stress levels.]] | ||
Latest revision as of 19:02, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.
This example appears in the Accelerated life testing reference.
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).