Operational Mission Profile Testing: Difference between revisions
| Line 37: | Line 37: | ||
<br> | <br> | ||
{|style= align="center" border="1" | {|style= align="center" border="1" | ||
| | |- | ||
|colspan="7" style="text-align:center"|Table 12.1 - Test-fix-find-test data | |||
|- | |||
!<math>i</math> | !<math>i</math> | ||
!<math>{{X}_{i}}</math> | !<math>{{X}_{i}}</math> | ||
| Line 105: | Line 107: | ||
<br> | <br> | ||
{|style= align="center" border="1" | {|style= align="center" border="1" | ||
| | |||
|colspan="7" style="text-align:center"|Table 12.2 - Expected and actual results for profiles 1, 2, 3 | |||
|- | |- | ||
| ||colspan="2" style="text-align: center;" | Profile 1(gun firings)|| colspan="2" style="text-align: center;" | Profile 2(E1)|| colspan="2" style="text-align: center;" | Profile 3(E2) | | ||colspan="2" style="text-align: center;" | Profile 1(gun firings)|| colspan="2" style="text-align: center;" | Profile 2(E1)|| colspan="2" style="text-align: center;" | Profile 3(E2) | ||
Revision as of 19:10, 18 August 2011
Operational Mission Profile Testing
It is common practice for systems to be subjected to operational testing during a development program. The objective of this testing is to evaluate the performance of the system, including reliability, under conditions that represent actual use. Because of budget, resources, schedule and other considerations, these operational tests rarely match exactly the actual use conditions. Usually, stated mission profile conditions are used for operational testing. These mission profile conditions are typically general statements that guide testing on an average basis. For example, a copier might be required to print 3,000 pages by time T=10 days and 5,000 pages by time T=15 days. In addition the copier is required to scan 200 documents by time T=10 days, 250 documents by time T=15 days, etc.
Because of practical constraints these full mission profile conditions are typically not repeated one after the other during testing. Instead, the elements that make up the mission profile conditions are tested under varying schedules with the intent that, on average, the mission profile conditions are met. In practice, reliability corrective actions are generally incorporated into the system as a result of this type of testing.
Because of a lack of structure for managing the elements that make up the mission profile, it is difficult to have an agreed upon methodology for estimating the system's reliability. Many systems fail operational testing because key assessments such as growth potential and projections cannot be made in a straightforward manner so that management can take appropriate action. RGA 7 addresses this issue by incorporating a systematic mission profile methodology for operational reliability testing and reliability growth assessments.
Introduction
Operational testing is an attempt to subject the system to conditions close to the actual environment that is expected under customer use. Often this is an extension of reliability growth testing where operation induced failure modes and corrective actions are of prime interest. Sometimes the stated intent is for a demonstration test where corrective actions are not the prime objective. However, it is not unusual for a system to fail the demonstration test, and the management issue is what to do next. In both cases, important valid key parameters are needed to properly assess this situation and make cost-effective and timely decisions. This is often difficult in practice.
For example, a system may be required to conduct a specific task a fixed number times for each hour of operation (task 1), be required to move a fixed number of miles under a specific operating condition for each hour of operation (task 2), and be required to move a fixed number of miles under another operating condition for each hour of operation (task 3). During operational testing these guidelines are met individually as averages. For example, the actual as-tested profile for task 1 may not be uniform relative to the stated mission guidelines during the testing. What is often the case is that some of the tasks (for example task 1) could be operated below the stated guidelines. This can mask a major reliability problem. In other cases during testing, tasks 1, 2 and 3 might never meet their stated averages, except perhaps at the end of the test. This becomes an issue because an important aspect of effective reliability risk management is not to wait until the end of the test to have an assessment of the reliability performance.
Because the elements of the mission profile during the testing will rarely, if ever, balance continuously to the stated averages, a common analysis method is to piece the reliability assessment together by evaluating each element of the profile separately. This is not a well-defined methodology and does not account for improvement during the testing. It is therefore not unusual for two separate organizations (e.g., the customer and the developer) to analyze the same data and have different MTBF numbers. In addition, this method does not address delayed corrective actions to be incorporated at the end of the test nor does it estimate growth potential or interaction effects. Therefore, to reduce this risk there is a need for a rigorous methodology for reliability during operational testing that does not rely on piecewise analysis and avoids the issues noted above.
RGA 7 incorporates a new methodology to manage system reliability during operational mission profile testing. This methodology draws information from particular plots of the operational test data and inserts key information into a growth model. This improved methodology does not piece the analysis together but gives a direct MTBF mission profile estimate of the system's reliability that is directly compared to the MTBF requirement. The methodology will reflect any reliability growth improvement during the test, and will also give management a projected higher MTBF for the system mission profile reliability after delayed corrected actions are incorporated at the end of the test. In addition, the methodology also gives an estimate of the system's growth potential, and provides management metrics to evaluate whether changes in the program need to be made. A key advantage is that the methodology is well-defined and all organizations will arrive at the same reliability assessment with the same data.
Testing Methodology
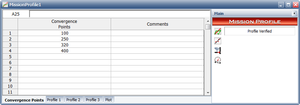
The methodology described here will use the Crow Extended model (presented in Chapter 9) for data analysis. In order to have valid Crow Extended model assessments, it is required that the operational mission profile be conducted in a structured manner. Therefore, this testing methodology involves convergence and stopping points during the testing. A stopping point is when the testing is stopped for the expressed purpose of incorporating the Type BD delayed corrective actions. There may be more than one stopping point during a particular testing phase. For simplicity, the methodology with only one stopping point will be described; however, the methodology can be extended to the case of more than one stopping point. A convergence point is a time during the test when all the operational mission profile tasks meet their expected averages or fall within an acceptable range. At least three convergence points are required for a well-balanced test. The end of the test, time [math]\displaystyle{ T }[/math] , must be a convergence point. The test times between the convergence points do not have to be the same.
The objective of having the convergence points is to be able to apply the Crow Extended model directly in such a way that the projection and other key reliability growth parameters can be estimated in a valid fashion. To do this, the grouped data methodology is applied. Note that the methodology also can be used with the Crow-AMSAA (NHPP) model for a simpler analysis without the ability to estimate projected and growth potential reliability. For the Crow-AMSAA (NHPP) grouped data methodology, refer to Chapter 5, Section 3. For grouped data using the Crow Extended model, refer to Chapter 9, Section 6.
Example
Consider the test-fix-find-test data of Example 2 in Chapter 9, which is shown again in Table 12.1. The total test time for this test is 400 hours. Note that for this example we assume one stopping point at the end of the test for the incorporation of the delayed fixes. Suppose that the data set represents a military system with Task 1 firing a gun, Task 2 moving under environment E1 and Task 3 moving under environment E2. For every hour of operation the operational profile states that the system operates in environment E1 70% of the time and in environment E2 30% of the time. In addition, for each hour of operation the gun must be fired 10 times.
In general, it is difficult to manage an operational test so that these operational profiles are continuously met throughout the test. However, the operational mission profile methodology requires that these conditions be met on average at the convergence points. In practice, this almost always can be done with proper program and test management. The convergence points are set for the testing, often at interim assessment points. The process for controlling the convergence at these points involves monitoring a graph for each of the tasks.
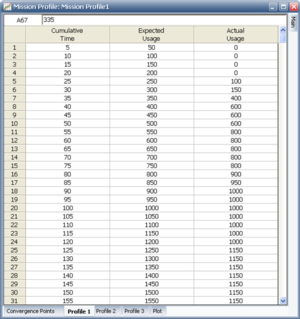
Table 12.2 shows the expected and actual results for each of the operational mission profiles.
| Table 12.1 - Test-fix-find-test data | ||||||
| [math]\displaystyle{ i }[/math] | [math]\displaystyle{ {{X}_{i}} }[/math] | Mode | [math]\displaystyle{ i }[/math] | [math]\displaystyle{ {{X}_{i}} }[/math] | Mode | |
|---|---|---|---|---|---|---|
| 1 | 0.7 | BC17 | 29 | 192.7 | BD11 | |
| 2 | 3.7 | BC17 | 30 | 213 | A | |
| 3 | 13.2 | BC17 | 31 | 244.8 | A | |
| 4 | 15 | BD1 | 32 | 249 | BD12 | |
| 5 | 17.6 | BC18 | 33 | 250.8 | A | |
| 6 | 25.3 | BD2 | 34 | 260.1 | BD1 | |
| 7 | 47.5 | BD3 | 35 | 263.5 | BD8 | |
| 8 | 54 | BD4 | 36 | 273.1 | A | |
| 9 | 54.5 | BC19 | 37 | 274.7 | BD6 | |
| 10 | 56.4 | BD5 | 38 | 282.8 | BC27 | |
| 11 | 63.6 | A | 39 | 285 | BD13 | |
| 12 | 72.2 | BD5 | 40 | 304 | BD9 | |
| 13 | 99.2 | BC20 | 41 | 315.4 | BD4 | |
| 14 | 99.6 | BD6 | 42 | 317.1 | A | |
| 15 | 100.3 | BD7 | 43 | 320.6 | A | |
| 16 | 102.5 | A | 44 | 324.5 | BD12 | |
| 17 | 112 | BD8 | 45 | 324.9 | BD10 | |
| 18 | 112.2 | BC21 | 46 | 342 | BD5 | |
| 19 | 120.9 | BD2 | 47 | 350.2 | BD3 | |
| 20 | 121.9 | BC22 | 48 | 355.2 | BC28 | |
| 21 | 125.5 | BD9 | 49 | 364.6 | BD10 | |
| 22 | 133.4 | BD10 | 50 | 364.9 | A | |
| 23 | 151 | BC23 | 51 | 366.3 | BD2 | |
| 24 | 163 | BC24 | 52 | 373 | BD8 | |
| 25 | 164.7 | BD9 | 53 | 379.4 | BD14 | |
| 26 | 174.5 | BC25 | 54 | 389 | BD15 | |
| 27 | 177.4 | BD10 | 55 | 394.9 | A | |
| 28 | 191.6 | BC26 | 56 | 395.2 | BD16 | |
| Table 12.2 - Expected and actual results for profiles 1, 2, 3 | ||||||
| Profile 1(gun firings) | Profile 2(E1) | Profile 3(E2) | ||||
| Time | Expected | Actual | Expected | Actual | Expected | Actual |
| 5 | 50 | 0 | 3.5 | 5 | 1.5 | 0 |
| 10 | 100 | 0 | 7 | 10 | 3 | 0 |
| 15 | 150 | 0 | 10.5 | 15 | 4.5 | 0 |
| 20 | 200 | 0 | 14 | 20 | 6 | 0 |
| 25 | 250 | 100 | 17.5 | 25 | 7.5 | 0 |
| 30 | 300 | 150 | 21 | 30 | 9 | 0 |
| 35 | 350 | 400 | 24.5 | 30 | 10.5 | 5 |
| 40 | 400 | 600 | 28 | 30 | 12 | 10 |
| 45 | 450 | 600 | 31.5 | 30 | 13.5 | 15 |
| 50 | 500 | 600 | 35 | 30 | 15 | 20 |
| 55 | 550 | 800 | 38.5 | 35 | 16.5 | 20 |
| 60 | 600 | 800 | 42 | 40 | 18 | 20 |
| 65 | 650 | 800 | 45.5 | 45 | 19.5 | 20 |
| 70 | 700 | 800 | 49 | 50 | 21 | 20 |
| 75 | 750 | 800 | 52.5 | 55 | 22.5 | 20 |
| 80 | 800 | 900 | 56 | 55 | 24 | 25 |
| 85 | 850 | 950 | 59.5 | 55 | 25.5 | 30 |
| 90 | 900 | 1000 | 63 | 60 | 27 | 30 |
| 95 | 950 | 1000 | 66.5 | 65 | 28.5 | 30 |
| 100 | 1000 | 1000 | 70 | 70 | 30 | 30 |
| 105 | 1050 | 1000 | 73.5 | 70 | 31.5 | 35 |
| ... | ... | ... | ... | ... | ... | |
| ... | ... | ... | ... | ... | ... | |
| 355 | 3550 | 3440 | 248.5 | 259 | 106.5 | 96 |
| 360 | 3600 | 3690 | 252 | 264 | 108 | 96 |
| 365 | 3650 | 3690 | 255.5 | 269 | 109.5 | 96 |
| 370 | 3700 | 3850 | 259 | 274 | 111 | 96 |
| 375 | 3750 | 3850 | 262.5 | 279 | 112.5 | 96 |
| 380 | 3800 | 3850 | 266 | 280 | 114 | 100 |
| 385 | 3850 | 3850 | 269.5 | 280 | 115.5 | 105 |
| 390 | 3900 | 3850 | 273 | 280 | 117 | 110 |
| 395 | 3950 | 4000 | 276.5 | 280 | 118.5 | 115 |
| 400 | 4000 | 4000 | 280 | 280 | 120 | 120 |
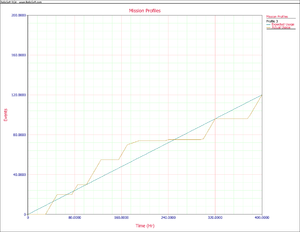
Figure Profile shows a portion of the expected and actual results for mission profile 1, as entered in RGA 7. A graph exists for each of the three tasks in this example. Each graph has a line with the expected average as a function of hours, and the corresponding actual value. When the actual value for a task meets the expected value then is a convergence for that task. A convergence point occurs when all of the tasks converge at the same time. At least three convergence points are required, one of which is the stopping point [math]\displaystyle{ T }[/math] . In our example, the total test time is 400 hours. The convergence points were chosen to be at 100, 250, 320 and 400 hours. Figure convergence points shows the data sheet that contains the convergence points in RGA 7.
[math]\displaystyle{ }[/math]
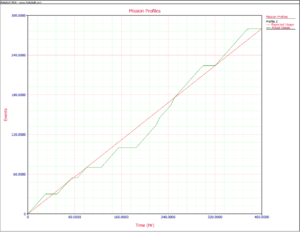
The testing profiles are managed so that at these times the actual operational test profile equals the expected values for the three tasks or falls within an acceptable range. Figure firings shows the expected and actual gun firings. Figure E1 shows the expected and actual time in environment E1 and Figure E2 shows the expected and actual time in environment E2.
[math]\displaystyle{ }[/math]
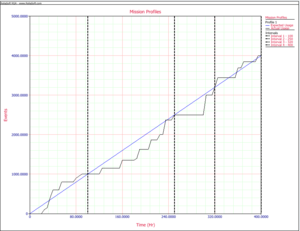
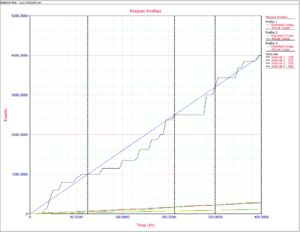
The objective of having the convergence points is to be able to apply the Crow Extended model directly in such a way that the projection and other key reliability growth parameters can be estimated in a valid fashion. To do this, grouped data is applied using the Crow Extended model. For reliability growth assessments using grouped data, only information between time points in the testing is used. In our application, these time points are the convergence points: 100, 250, 320, and 400. Figure Combinedission shows all three mission profiles plotted in the same graph, together with the convergence points.
Table 12.3 gives the grouped data input corresponding to the data in Table 12.1.
The parameters of the Crow Extended model for grouped data are then estimated, as explained in Chapter 9, Section 6. Table 12.4 shows the effectiveness factors (EFs) for each of the BD modes.
| Table 12.3 - Grouped data at convergence points 100, 250, 320 and 400 hours | ||||||||
| Number at Event | Time to Event | Classification | Mode | Number at Event | Time to Event | Classification | Mode | |
|---|---|---|---|---|---|---|---|---|
| 3 | 100 | BC | 17 | 1 | 250 | BC | 26 | |
| 1 | 100 | BD | 1 | 1 | 250 | BD | 11 | |
| 1 | 100 | BC | 18 | 1 | 250 | BD | 12 | |
| 1 | 100 | BD | 2 | 3 | 320 | A | ||
| 1 | 100 | BD | 3 | 1 | 320 | BD | 1 | |
| 1 | 100 | BD | 4 | 1 | 320 | BD | 8 | |
| 1 | 100 | BC | 19 | 1 | 320 | BD | 6 | |
| 2 | 100 | BD | 5 | 1 | 320 | BC | 27 | |
| 1 | 100 | A | 1 | 320 | BD | 13 | ||
| 1 | 100 | BC | 20 | 1 | 320 | BD | 9 | |
| 1 | 100 | BD | 6 | 1 | 320 | BD | 4 | |
| 1 | 250 | BD | 7 | 3 | 400 | A | ||
| 3 | 250 | A | 1 | 400 | BD | 12 | ||
| 1 | 250 | BD | 8 | 2 | 400 | BD | 10 | |
| 1 | 250 | BC | 21 | 1 | 400 | BD | 5 | |
| 1 | 250 | BD | 2 | 1 | 400 | BD | 3 | |
| 1 | 250 | BC | 22 | 1 | 400 | BC | 28 | |
| 2 | 250 | BD | 9 | 1 | 400 | BD | 2 | |
| 2 | 250 | BD | 10 | 1 | 400 | BD | 8 | |
| 1 | 250 | BC | 23 | 1 | 400 | BD | 14 | |
| 1 | 250 | BC | 24 | 1 | 400 | BD | 15 | |
| 1 | 250 | BC | 25 | 1 | 400 | BD | 16 | |
| Table 12.4 - Effectiveness Factors for delayed fixes | |
| Mode | Effectiveness Factor |
|---|---|
| 1 | 0.67 |
| 2 | 0.72 |
| 3 | 0.77 |
| 4 | 0.77 |
| 5 | 0.87 |
| 6 | 0.92 |
| 7 | 0.50 |
| 8 | 0.85 |
| 9 | 0.89 |
| 10 | 0.74 |
| 11 | 0.70 |
| 12 | 0.63 |
| 13 | 0.64 |
| 14 | 0.72 |
| 15 | 0.69 |
| 16 | 0.46 |
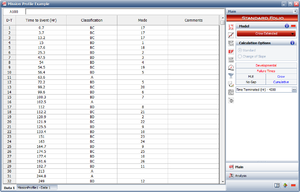
Using the Crow Extended failure times Data Sheet shown in Figure Failure times data, we can analyze this data set based on a mission profile by clicking the mission profile icon:
[math]\displaystyle{ }[/math]
[math]\displaystyle{ }[/math]
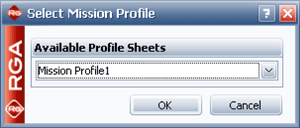
A specific mission profile can then be associated with the Data Sheet, as shown in Figure selecting. This will group the failure times data into groups based on the convergence points that have already been specified when constructing the mission profile.
[math]\displaystyle{ }[/math]
A new data sheet with the grouped data is created, as shown in Figure groupedata.
The calculated results based on the grouped data are as follows:
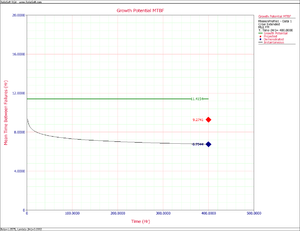
Figure growth potential shows the instantaneous, demonstrated, projected and growth potential MTBF for the grouped data, based the mission profile grouping with intervals at the specified convergence points of the mission profile.