Exponential Distribution for Grouped Data Example: Difference between revisions
Chris Kahn (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude> | <noinclude> | ||
{{Banner Weibull Examples}} | {{Banner Weibull Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/life_data_analysis Life data analysis reference]''. | ||
</noinclude> | </noinclude> | ||
20 units were reliability tested with the following results: | |||
{| border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | {| border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | ||
|- | |- | ||
|colspan="2" style="text-align:center"| Table - Life Test Data | |colspan="2" style="text-align:center"| '''Table - Life Test Data''' | ||
|- | |- | ||
|-align="center" | |-align="center" | ||
| Line 27: | Line 28: | ||
|} | |} | ||
1. Assuming a 2-parameter exponential distribution, estimate the parameters by hand using the MLE analysis method. | |||
2. Repeat the above using Weibull++. (Enter the data as grouped data to duplicate the results.) | |||
3. Show the Probability plot for the analysis results. | |||
4. Show the Reliability vs. Time plot for the results. | |||
5. Show the ''pdf'' plot for the results. | |||
6. Show the Failure Rate vs. Time plot for the results. | |||
7. Estimate the parameters using the rank regression on Y (RRY) analysis method (and using grouped ranks). | |||
'''Solution''' | '''Solution''' | ||
1. For the 2-parameter exponential distribution and for <math>\hat{\gamma }=100\,\!</math> hours (first failure), the partial of the log-likelihood function, <math>\lambda\,\!</math>, becomes: | |||
::<math> \begin{align} | ::<math> \begin{align} | ||
| Line 56: | Line 58: | ||
\end{align} | \end{align} | ||
</math> | \,\!</math> | ||
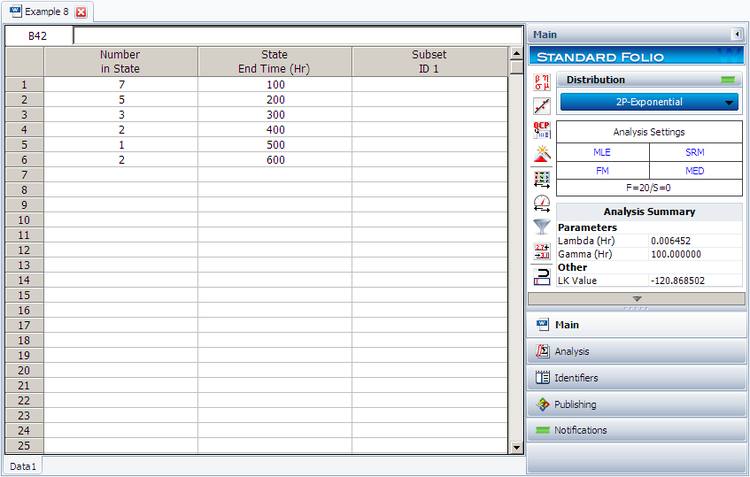
2. Enter the data in a Weibull++ standard folio and calculate it as shown next. | |||
<br> | <br> | ||
<br> | <br> | ||
[[Image:Exponential Distribution Example 8 Data.png|center| | [[Image:Exponential Distribution Example 8 Data.png|center|750px|]] | ||
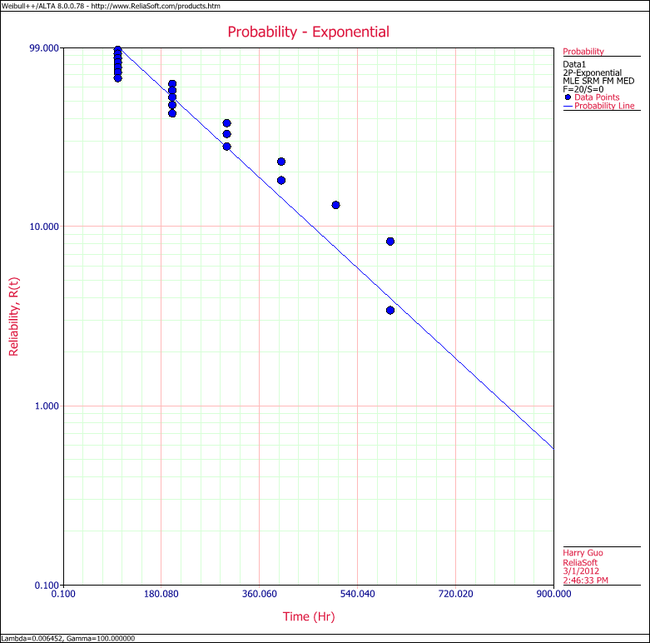
3. On the Plot page of the folio, the exponential Probability plot will appear as shown next. | |||
[[Image:Exponential Distribution Example 8 Plot.png|center|650px|]] | |||
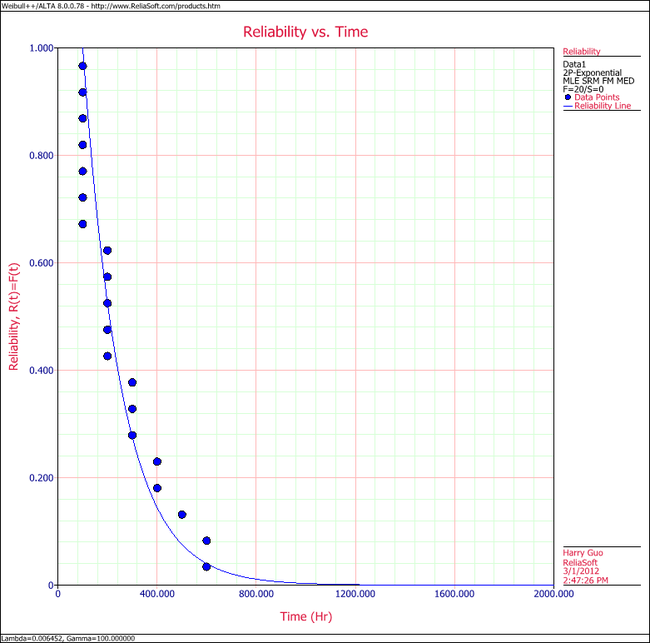
4. View the Reliability vs. Time plot. | |||
[[Image:Exponential Distribution Example 8 Rel Plot.png|center|650px|]] | |||
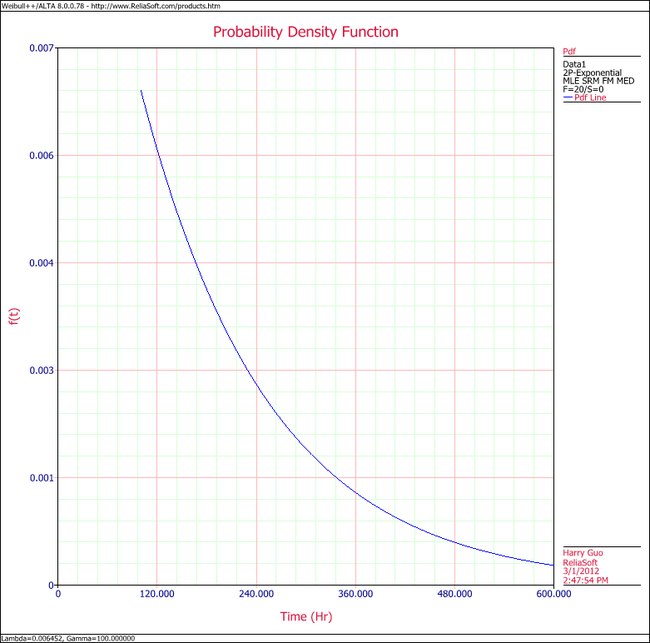
5. View the ''pdf'' plot. | |||
[[Image:Exponential Distribution Example 8 Pdf Plot.png|center|650px|]] | |||
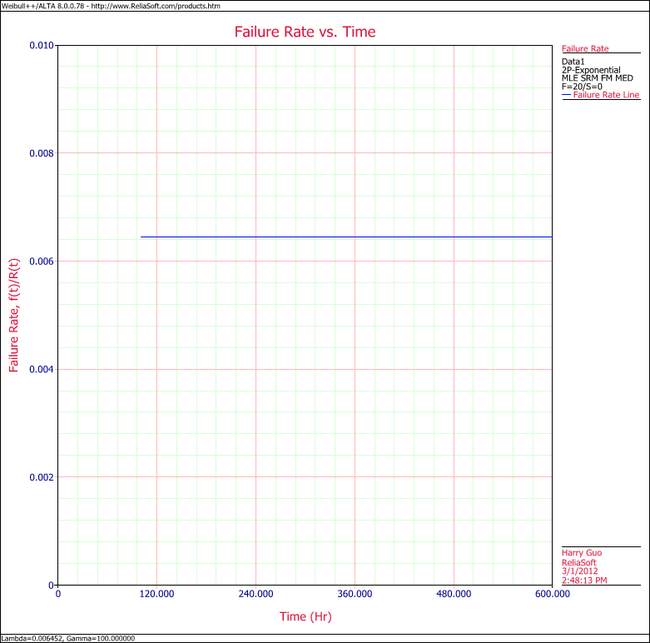
6. View the Failure Rate vs. Time plot. | |||
[[Image:Exponential Distribution Example 8 Failure Rate Plot.png|center|650px|]] | |||
Note that, as described at the beginning of this chapter, the failure rate for the exponential distribution is constant. Also note that the Failure Rate vs. Time plot does show values for times before the location parameter, <math>\gamma \,\!</math>, at 100 hours. | |||
7. In the case of grouped data, one must be cautious when estimating the parameters using a rank regression method. This is because the median rank values are determined from the total number of failures observed by time <math>{{T}_{i}}\,\!</math> where <math>i\,\!</math> indicates the group number. In this example, the total number of groups is <math>N=6\,\!</math> and the total number of units is <math>{{N}_{T}}=20\,\!</math>. Thus, the median rank values will be estimated for 20 units and for the total failed units (<math>{{N}_{{{F}_{i}}}}\,\!</math>) up to the <math>{{i}^{th}}\,\!</math> group, for the <math>{{i}^{th}}\,\!</math> rank value. The median ranks values can be found from rank tables or they can be estimated using ReliaSoft's Quick Statistical Reference tool. | |||
For example, the median rank value of the fourth group will be the <math>{{17}^{th}}\,\!</math> rank out of a sample size of twenty units (or 81.945%). | |||
The following table is then constructed. | |||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 105: | Line 113: | ||
\text{6} & \text{2} & \text{20} & \text{600} & \text{0}\text{.96594} & \text{-3}\text{.3795} & \text{360000} & \text{11}\text{.4211} & \text{-2027}\text{.7085} \\ | \text{6} & \text{2} & \text{20} & \text{600} & \text{0}\text{.96594} & \text{-3}\text{.3795} & \text{360000} & \text{11}\text{.4211} & \text{-2027}\text{.7085} \\ | ||
\sum_{}^{} & {} & {} & \text{2100} & {} & \text{-9}\text{.6476} & \text{910000} & \text{20}\text{.9842} & \text{-4320}\text{.3362} \\ | \sum_{}^{} & {} & {} & \text{2100} & {} & \text{-9}\text{.6476} & \text{910000} & \text{20}\text{.9842} & \text{-4320}\text{.3362} \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
Given the values in the table above, calculate <math>\hat{a}</math> and <math>\hat{b}</math>: | Given the values in the table above, calculate <math>\hat{a}\,\!</math> and <math>\hat{b}\,\!</math>: | ||
| Line 115: | Line 123: | ||
& & \\ | & & \\ | ||
& \hat{b}= & \frac{-4320.3362-(2100)(-9.6476)/6}{910,000-{{(2100)}^{2}}/6} | & \hat{b}= & \frac{-4320.3362-(2100)(-9.6476)/6}{910,000-{{(2100)}^{2}}/6} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
or: | or: | ||
::<math>\hat{b}=-0.005392</math> | ::<math>\hat{b}=-0.005392\,\!</math> | ||
and: | and: | ||
::<math>\hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N}</math> | ::<math>\hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N}\,\!</math> | ||
or: | or: | ||
::<math>\hat{a}=\frac{-9.6476}{6}-(-0.005392)\frac{2100}{6}=0.2793</math> | ::<math>\hat{a}=\frac{-9.6476}{6}-(-0.005392)\frac{2100}{6}=0.2793\,\!</math> | ||
Therefore: | Therefore: | ||
::<math>\hat{\lambda }=-\hat{b}=-(-0.005392)=0.05392\text{ failures/hour}</math> | ::<math>\hat{\lambda }=-\hat{b}=-(-0.005392)=0.05392\text{ failures/hour}\,\!</math> | ||
and: | and: | ||
::<math>\hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2793}{0.005392}</math> | ::<math>\hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2793}{0.005392}\,\!</math> | ||
or: | or: | ||
::<math>\hat{\gamma }\simeq 51.8\text{ hours}</math> | ::<math>\hat{\gamma }\simeq 51.8\text{ hours}\,\!</math> | ||
Then: | Then: | ||
::<math>f(T)=(0.005392){{e}^{-0.005392(T-51.8)}}</math> | ::<math>f(T)=(0.005392){{e}^{-0.005392(T-51.8)}}\,\!</math> | ||
Using Weibull++ , the estimated parameters are: | |||
Using Weibull++, the estimated parameters are: | |||
::<math>\begin{align} | ::<math>\begin{align} | ||
\hat{\lambda }= & 0.0054\text{ failures/hour} \\ | \hat{\lambda }= & 0.0054\text{ failures/hour} \\ | ||
\hat{\gamma }= & 51.82\text{ hours} | \hat{\gamma }= & 51.82\text{ hours} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
The small difference in the values from Weibull++ is due to rounding. In | The small difference in the values from Weibull++ is due to rounding. In the application, the calculations and the rank values are carried out up to the <math>15^{th}\,\!</math> decimal point. | ||
Latest revision as of 21:46, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
This example appears in the Life data analysis reference.
20 units were reliability tested with the following results:
| Table - Life Test Data | |
| Number of Units in Group | Time-to-Failure |
|---|---|
| 7 | 100 |
| 5 | 200 |
| 3 | 300 |
| 2 | 400 |
| 1 | 500 |
| 2 | 600 |
1. Assuming a 2-parameter exponential distribution, estimate the parameters by hand using the MLE analysis method.
2. Repeat the above using Weibull++. (Enter the data as grouped data to duplicate the results.)
3. Show the Probability plot for the analysis results.
4. Show the Reliability vs. Time plot for the results.
5. Show the pdf plot for the results.
6. Show the Failure Rate vs. Time plot for the results.
7. Estimate the parameters using the rank regression on Y (RRY) analysis method (and using grouped ranks).
Solution
1. For the 2-parameter exponential distribution and for [math]\displaystyle{ \hat{\gamma }=100\,\! }[/math] hours (first failure), the partial of the log-likelihood function, [math]\displaystyle{ \lambda\,\! }[/math], becomes:
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \lambda }= &\underset{i=1}{\overset{6}{\mathop \sum }}\,{N_i} \left[ \frac{1}{\lambda }-\left( {{T}_{i}}-100 \right) \right]=0\\ \Rightarrow & 7[\frac{1}{\lambda }-(100-100)]+5[\frac{1}{\lambda}-(200-100)] + \ldots +2[\frac{1}{\lambda}-(600-100)]\\ = & 0\\ \Rightarrow & \hat{\lambda}=\frac{20}{3100}=0.0065 \text{fr/hr} \end{align} \,\! }[/math]
2. Enter the data in a Weibull++ standard folio and calculate it as shown next.
3. On the Plot page of the folio, the exponential Probability plot will appear as shown next.
4. View the Reliability vs. Time plot.
5. View the pdf plot.
6. View the Failure Rate vs. Time plot.
Note that, as described at the beginning of this chapter, the failure rate for the exponential distribution is constant. Also note that the Failure Rate vs. Time plot does show values for times before the location parameter, [math]\displaystyle{ \gamma \,\! }[/math], at 100 hours.
7. In the case of grouped data, one must be cautious when estimating the parameters using a rank regression method. This is because the median rank values are determined from the total number of failures observed by time [math]\displaystyle{ {{T}_{i}}\,\! }[/math] where [math]\displaystyle{ i\,\! }[/math] indicates the group number. In this example, the total number of groups is [math]\displaystyle{ N=6\,\! }[/math] and the total number of units is [math]\displaystyle{ {{N}_{T}}=20\,\! }[/math]. Thus, the median rank values will be estimated for 20 units and for the total failed units ([math]\displaystyle{ {{N}_{{{F}_{i}}}}\,\! }[/math]) up to the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group, for the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] rank value. The median ranks values can be found from rank tables or they can be estimated using ReliaSoft's Quick Statistical Reference tool.
For example, the median rank value of the fourth group will be the [math]\displaystyle{ {{17}^{th}}\,\! }[/math] rank out of a sample size of twenty units (or 81.945%).
The following table is then constructed.
Given the values in the table above, calculate [math]\displaystyle{ \hat{a}\,\! }[/math] and [math]\displaystyle{ \hat{b}\,\! }[/math]:
- [math]\displaystyle{ \begin{align} & \hat{b}= & \frac{\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}}{{y}_{i}}-(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}})(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{y}_{i}})/6}{\underset{i=1}{\overset{6}{\mathop{\sum }}}\,t_{i}^{2}-{{(\underset{i=1}{\overset{6}{\mathop{\sum }}}\,{{t}_{i}})}^{2}}/6} \\ & & \\ & \hat{b}= & \frac{-4320.3362-(2100)(-9.6476)/6}{910,000-{{(2100)}^{2}}/6} \end{align}\,\! }[/math]
or:
- [math]\displaystyle{ \hat{b}=-0.005392\,\! }[/math]
and:
- [math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{t}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{t}_{i}}}{N}\,\! }[/math]
or:
- [math]\displaystyle{ \hat{a}=\frac{-9.6476}{6}-(-0.005392)\frac{2100}{6}=0.2793\,\! }[/math]
Therefore:
- [math]\displaystyle{ \hat{\lambda }=-\hat{b}=-(-0.005392)=0.05392\text{ failures/hour}\,\! }[/math]
and:
- [math]\displaystyle{ \hat{\gamma }=\frac{\hat{a}}{\hat{\lambda }}=\frac{0.2793}{0.005392}\,\! }[/math]
or:
- [math]\displaystyle{ \hat{\gamma }\simeq 51.8\text{ hours}\,\! }[/math]
Then:
- [math]\displaystyle{ f(T)=(0.005392){{e}^{-0.005392(T-51.8)}}\,\! }[/math]
Using Weibull++, the estimated parameters are:
- [math]\displaystyle{ \begin{align} \hat{\lambda }= & 0.0054\text{ failures/hour} \\ \hat{\gamma }= & 51.82\text{ hours} \end{align}\,\! }[/math]
The small difference in the values from Weibull++ is due to rounding. In the application, the calculations and the rank values are carried out up to the [math]\displaystyle{ 15^{th}\,\! }[/math] decimal point.