Variable Throughput Example: Difference between revisions
Kate Racaza (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner BlockSim Examples}} | <noinclude>{{Banner BlockSim Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/system_analysis System analysis reference]''. | ||
<!-- THE RBDs IN THIS PAGE ARE LINKED TO ANOTHER EXAMPLE. IF YOU CHANGE THE PROPERTIES OF THE RBDs IN THIS PAGE, YOU MUST ALSO UPDATE THE RBDs AND RESULTS IN: Constant Throughput Example. --> | <!-- THE RBDs IN THIS PAGE ARE LINKED TO ANOTHER EXAMPLE. IF YOU CHANGE THE PROPERTIES OF THE RBDs IN THIS PAGE, YOU MUST ALSO UPDATE THE RBDs AND RESULTS IN: Constant Throughput Example. --> | ||
To examine variable throughput in phase diagrams, consider a phase diagram of three phases with linked RBDs, as shown in the figure below. Each phase has a duration of 10 hours and all phases are set to continue simulation upon failure. Blocks A through E process a number of items per hour as identified next to each letter (e.g., A:10 implies that 10 units are processed per hour by block A). For the first phase, P1, the variable throughput model used is <math>y = x\,\!</math> (which is the linear model <math>y = ax+ b\,\!</math> with parameters <math>a = 1\,\! </math> and <math>b = 0\,\!</math>). For the second phase, P2, the model used is <math>y = 3x\,\!</math> (which is the linear model <math>y = ax+ b\,\! </math> with parameters <math>a = 3\,\! </math> and <math>b = 0\,\! </math>). The third phase uses <math>y = 0.5x\,\!</math> as the variable throughput model (which is the linear model <math>y = ax + b\,\!</math> with parameters <math>a = 0.5\,\!</math> and <math>b = 0\,\!</math>). Phases P1 and P2 have a value of 500 units per hour set for the maximum throughput capacity. This relatively larger value of throughput is set for the two phases so that the phases do not reach their maximum throughput value during the simulation. Phase P3 has a value of 4 units per hour set as the maximum throughput capacity. For the sake of simplicity it is assumed that the blocks can never fail and that items are routed equally to each path. The ignore backlog option is left unchecked for all blocks in the phase diagram. | To examine variable throughput in phase diagrams, consider a phase diagram of three phases with linked RBDs, as shown in the figure below. Each phase has a duration of 10 hours and all phases are set to continue simulation upon failure. Blocks A through E process a number of items per hour as identified next to each letter (e.g., A:10 implies that 10 units are processed per hour by block A). For the first phase, P1, the variable throughput model used is <math>y = x\,\!</math> (which is the linear model <math>y = ax+ b\,\!</math> with parameters <math>a = 1\,\!</math> and <math>b = 0\,\!</math>). For the second phase, P2, the model used is <math>y = 3x\,\!</math> (which is the linear model <math>y = ax+ b\,\!</math> with parameters <math>a = 3\,\!</math> and <math>b = 0\,\!</math>). The third phase uses <math>y = 0.5x\,\!</math> as the variable throughput model (which is the linear model <math>y = ax + b\,\!</math> with parameters <math>a = 0.5\,\!</math> and <math>b = 0\,\!</math>). Phases P1 and P2 have a value of 500 units per hour set for the maximum throughput capacity. This relatively larger value of throughput is set for the two phases so that the phases do not reach their maximum throughput value during the simulation. Phase P3 has a value of 4 units per hour set as the maximum throughput capacity. For the sake of simplicity it is assumed that the blocks can never fail and that items are routed equally to each path. The ignore backlog option is left unchecked for all blocks in the phase diagram. | ||
[[Image:11.21b.png|center|700px]]</noinclude> | [[Image:11.21b.png|center|700px|link=]]</noinclude> | ||
<includeonly>To examine variable throughput in phase diagrams, consider the phase diagram used above in the constant throughput example. All phase properties and linked RBDs remain unchanged for this illustration except that all the three phases now use variable throughput models. For the first phase, P1, the variable throughput model used is <math>y = x\,\!</math> (which is the linear model <math>y = ax+ b\,\!</math> with parameters <math>a = 1\,\! </math> and <math>b = 0\,\!</math>). For the second phase, P2, the model used is <math>y = 3x\,\!</math> (which is the linear model <math>y = ax+ b\,\! </math> with parameters <math>a = 3\,\! </math> and <math>b = 0\,\! </math>). The third phase uses <math>y = 0.5x\,\!</math> as the variable throughput model (which is the linear model <math>y = ax + b\,\!</math> with parameters <math>a = 0.5\,\!</math> and <math>b = 0\,\!</math>). Phases P1 and P2 have a value of 500 units per hour set for the maximum throughput capacity. This relatively larger value of throughput is set for the two phases so that the phases do not reach their maximum throughput value during the simulation. Phase P3 has a value of 4 units per hour set as the maximum throughput capacity. As in the previous example, all phases have a duration of ten hours. For the sake of simplicity it is assumed that the blocks can never fail and that items are routed equally to each path. The ignore backlog option is left unchecked for all blocks in the phase diagram. </includeonly> | <includeonly>To examine variable throughput in phase diagrams, consider the phase diagram used above in the constant throughput example. All phase properties and linked RBDs remain unchanged for this illustration except that all the three phases now use variable throughput models. For the first phase, P1, the variable throughput model used is <math>y = x\,\!</math> (which is the linear model <math>y = ax+ b\,\!</math> with parameters <math>a = 1\,\!</math> and <math>b = 0\,\!</math>). For the second phase, P2, the model used is <math>y = 3x\,\!</math> (which is the linear model <math>y = ax+ b\,\!</math> with parameters <math>a = 3\,\!</math> and <math>b = 0\,\!</math>). The third phase uses <math>y = 0.5x\,\!</math> as the variable throughput model (which is the linear model <math>y = ax + b\,\!</math> with parameters <math>a = 0.5\,\!</math> and <math>b = 0\,\!</math>). Phases P1 and P2 have a value of 500 units per hour set for the maximum throughput capacity. This relatively larger value of throughput is set for the two phases so that the phases do not reach their maximum throughput value during the simulation. Phase P3 has a value of 4 units per hour set as the maximum throughput capacity. As in the previous example, all phases have a duration of ten hours. For the sake of simplicity it is assumed that the blocks can never fail and that items are routed equally to each path. The ignore backlog option is left unchecked for all blocks in the phase diagram. </includeonly> | ||
[[Image:11.21.png|center| | [[Image:11.21.png|center|500px|link=]] | ||
| Line 24: | Line 24: | ||
= & \frac{1}{2}({{1}^{2}}-{{0}^{2}})+0(1-0) \\ | = & \frac{1}{2}({{1}^{2}}-{{0}^{2}})+0(1-0) \\ | ||
= & 0.5\text{ }units | = & 0.5\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 33: | Line 33: | ||
= & \frac{1}{2}({{2}^{2}}-{{1}^{2}})+0(2-1) \\ | = & \frac{1}{2}({{2}^{2}}-{{1}^{2}})+0(2-1) \\ | ||
= & 1.5\text{ }units | = & 1.5\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:::It can be seen that the throughput from phase P1 sent to block A increases with time. But the capacity of block A remains constant at 10 units per hour during the entire phase P1. Thus, it becomes important to know the point of time when the number of units sent by P1 exceed the capacity of block A and the block starts accumulating a backlog. This can be obtained by solving the throughput model for phase P1 <math>(y = x)\,\!</math> using the capacity of block A by substituting <math>y\,\!</math> as the block capacity as shown next: | :::It can be seen that the throughput from phase P1 sent to block A increases with time. But the capacity of block A remains constant at 10 units per hour during the entire phase P1. Thus, it becomes important to know the point of time when the number of units sent by P1 exceed the capacity of block A and the block starts accumulating a backlog. This can be obtained by solving the throughput model for phase P1 <math>(y = x)\,\!</math> using the capacity of block A by substituting <math>y\,\!</math> as the block capacity as shown next: | ||
| Line 40: | Line 40: | ||
y= & x \\ | y= & x \\ | ||
or\text{ }10= & x | or\text{ }10= & x | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:::Thus, at time <math>x = 10\,\!</math> hours the number of units supplied per hour by phase P1 will equal the capacity of block A. At this point of time block A will function to its full capacity with no excess capacity and no backlog. Beyond this point the units sent by phase P1 will exceed the capacity of block A and the block will start accumulating a backlog. Since the duration of phase P1 is 10 hours, backlog at block A will not be a concern in this phase because up to this time the capacity of the block exceeds the units sent by phase P1. Thus, the total units sent by phase P1 to block A during the phase duration of 10 hours is: | :::Thus, at time <math>x = 10\,\!</math> hours the number of units supplied per hour by phase P1 will equal the capacity of block A. At this point of time block A will function to its full capacity with no excess capacity and no backlog. Beyond this point the units sent by phase P1 will exceed the capacity of block A and the block will start accumulating a backlog. Since the duration of phase P1 is 10 hours, backlog at block A will not be a concern in this phase because up to this time the capacity of the block exceeds the units sent by phase P1. Thus, the total units sent by phase P1 to block A during the phase duration of 10 hours is: | ||
| Line 48: | Line 48: | ||
= & \frac{1}{2}({{10}^{2}}-{{0}^{2}})+0(10-0) \\ | = & \frac{1}{2}({{10}^{2}}-{{0}^{2}})+0(10-0) \\ | ||
= & 50\text{ }units | = & 50\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:::The total number of units that can be processed by block A (or the capacity of A) during phase P1 is: | :::The total number of units that can be processed by block A (or the capacity of A) during phase P1 is: | ||
| Line 55: | Line 55: | ||
= & 10\times 10 \\ | = & 10\times 10 \\ | ||
= & 100\text{ }units | = & 100\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
:::Thus, during the first phase, block A processes all 50 units sent by phase P1 with an excess capacity of 50 units (100-50=50 units). | :::Thus, during the first phase, block A processes all 50 units sent by phase P1 with an excess capacity of 50 units (100-50=50 units). | ||
| Line 69: | Line 69: | ||
[[Image:11t12.png|center| | [[Image:11t12.png|center|800px|link=]] | ||
| Line 79: | Line 79: | ||
or\text{ }6= & 3x \\ | or\text{ }6= & 3x \\ | ||
or\text{ }x= & 2 | or\text{ }x= & 2 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Thus, at <math>x = 2\,\!</math> hours of phase P2 (or at the total simulation time of 12 hours), the number of units sent per hour by phase P2 equals the capacity of block A. Thus, during the first two hours of phase P2, block A will have excess capacity. The total number of units sent by phase P2 during the first two hours of the phase is: | ::Thus, at <math>x = 2\,\!</math> hours of phase P2 (or at the total simulation time of 12 hours), the number of units sent per hour by phase P2 equals the capacity of block A. Thus, during the first two hours of phase P2, block A will have excess capacity. The total number of units sent by phase P2 during the first two hours of the phase is: | ||
| Line 87: | Line 87: | ||
= & \frac{3}{2}({{2}^{2}}-{{0}^{2}})+0(2-0) \\ | = & \frac{3}{2}({{2}^{2}}-{{0}^{2}})+0(2-0) \\ | ||
= & 6\text{ }units | = & 6\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::The total capacity of block A during the first two hours of phase P2 is: | ::The total capacity of block A during the first two hours of phase P2 is: | ||
| Line 94: | Line 94: | ||
= & 6\times 2 \\ | = & 6\times 2 \\ | ||
= & 12\text{ }units | = & 12\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Thus block A processes a total of 6 units in the first two hours of phase P2 with an excess capacity of 6 units (12-6=6 units). During the last eight hours of the phase (from the second hour to the tenth hour) block A will have a backlog because the number of units sent by phase P2 will exceed block A's capacity. The total number of units sent by phase P2 during the last eight hours of the phase is: | ::Thus block A processes a total of 6 units in the first two hours of phase P2 with an excess capacity of 6 units (12-6=6 units). During the last eight hours of the phase (from the second hour to the tenth hour) block A will have a backlog because the number of units sent by phase P2 will exceed block A's capacity. The total number of units sent by phase P2 during the last eight hours of the phase is: | ||
| Line 102: | Line 102: | ||
= & \frac{3}{2}({{10}^{2}}-{{2}^{2}})+0(10-2) \\ | = & \frac{3}{2}({{10}^{2}}-{{2}^{2}})+0(10-2) \\ | ||
= & 144\text{ }units | = & 144\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::The total capacity of block A during these eight hours of phase P2 is: | ::The total capacity of block A during these eight hours of phase P2 is: | ||
| Line 109: | Line 109: | ||
= & 6\times 8 \\ | = & 6\times 8 \\ | ||
= & 48\text{ }units | = & 48\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
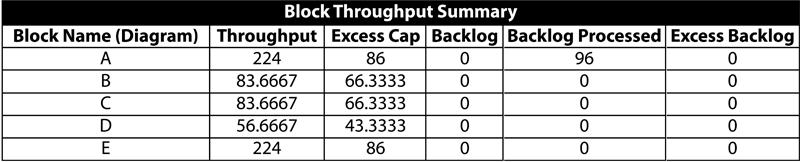
::Thus, during the last eight hours of phase P2, block A will process a total of 48 units with a backlog of 96 units (144-48=96 units). A graphical representation of the above scenario for block A during phase P2 is shown in the figure below. | ::Thus, during the last eight hours of phase P2, block A will process a total of 48 units with a backlog of 96 units (144-48=96 units). A graphical representation of the above scenario for block A during phase P2 is shown in the figure below. | ||
[[Image:11.22.png|center|550px]] | [[Image:11.22.png|center|550px|link=]] | ||
| Line 122: | Line 122: | ||
= & 5\times 2 \\ | = & 5\times 2 \\ | ||
= & 10\text{ }units | = & 10\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::As a result, blocks B and D each process 3 units in the first two hours of phase P2 with an excess capacity of 7 units (10-3=7 units). During the last eight hours of phase P2, block A sends a total of 48 units to blocks B and D, with each block receiving 24 units. The capacity of each of these blocks during these eight hours is: | ::As a result, blocks B and D each process 3 units in the first two hours of phase P2 with an excess capacity of 7 units (10-3=7 units). During the last eight hours of phase P2, block A sends a total of 48 units to blocks B and D, with each block receiving 24 units. The capacity of each of these blocks during these eight hours is: | ||
| Line 129: | Line 129: | ||
= & 5\times 8 \\ | = & 5\times 8 \\ | ||
= & 40\text{ }units | = & 40\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Thus, B and D process 24 units in the last eight hours of phase P2, with an excess capacity of 16 units (40-24=16 units). | ::Thus, B and D process 24 units in the last eight hours of phase P2, with an excess capacity of 16 units (40-24=16 units). | ||
| Line 139: | Line 139: | ||
= & 6\times 2 \\ | = & 6\times 2 \\ | ||
= & 12\text{ }units | = & 12\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Consequently block E processes 6 units in the first two hours of phase P2 with an excess capacity of 6 units (12-6=6 units). During the last eight hours of the phase, blocks B and D send a total of 48 units to block E. The capacity of block E during this time is: | ::Consequently block E processes 6 units in the first two hours of phase P2 with an excess capacity of 6 units (12-6=6 units). During the last eight hours of the phase, blocks B and D send a total of 48 units to block E. The capacity of block E during this time is: | ||
| Line 146: | Line 146: | ||
= & 6\times 8 \\ | = & 6\times 8 \\ | ||
= & 48\text{ }units | = & 48\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Thus, block E processes 48 units in the last eight hours of P2 with no excess capacity and no backlog. At 20 hrs phase P2 ends and phase P3 begins. | ::Thus, block E processes 48 units in the last eight hours of P2 with no excess capacity and no backlog. At 20 hrs phase P2 ends and phase P3 begins. | ||
| Line 153: | Line 153: | ||
:A summary result table for phase P2 is shown next. | :A summary result table for phase P2 is shown next. | ||
[[Image:11t13.png|center| | [[Image:11t13.png|center|800px|link=]] | ||
| Line 163: | Line 163: | ||
or\text{ }4= & 0.5x \\ | or\text{ }4= & 0.5x \\ | ||
or\text{ }x= & 8 | or\text{ }x= & 8 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Thus, at time <math>x = 8\,\!</math> hours of phase P3 (or at the time of 28 hours) the number of units sent per hour by phase P3 will reach the constant value of 4 units per hour. In the first eight hours of the phase the throughput will remain variable. The total number of units sent by P3 to block A during this time is given by: | ::Thus, at time <math>x = 8\,\!</math> hours of phase P3 (or at the time of 28 hours) the number of units sent per hour by phase P3 will reach the constant value of 4 units per hour. In the first eight hours of the phase the throughput will remain variable. The total number of units sent by P3 to block A during this time is given by: | ||
| Line 171: | Line 171: | ||
= & \frac{0.5}{2}({{8}^{2}}-{{0}^{2}})+0(8-0) \\ | = & \frac{0.5}{2}({{8}^{2}}-{{0}^{2}})+0(8-0) \\ | ||
= & 16\text{ }units | = & 16\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::The total capacity of block A during the first eight hours of phase P3 is: | ::The total capacity of block A during the first eight hours of phase P3 is: | ||
| Line 178: | Line 178: | ||
= & 15\times 8 \\ | = & 15\times 8 \\ | ||
= & 120\text{ }units | = & 120\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Consequently, it can be seen that block A has an excess capacity of 104 units (120-16=104 units). Thus, block A will be able to process all of the 96 units of backlog from phase P2 during these eight hours. As a result, block A will process a total of 112 units (16 units from P3 and 96 units from the backlog of phase P2) with an excess capacity of 8 units (120-112=8 units) during the first eight hours of phase P3. In the last two hours of this phase, a constant throughput of 4 units per hour is sent to block A, thus the total number of units sent to the block during the last two hours are: | ::Consequently, it can be seen that block A has an excess capacity of 104 units (120-16=104 units). Thus, block A will be able to process all of the 96 units of backlog from phase P2 during these eight hours. As a result, block A will process a total of 112 units (16 units from P3 and 96 units from the backlog of phase P2) with an excess capacity of 8 units (120-112=8 units) during the first eight hours of phase P3. In the last two hours of this phase, a constant throughput of 4 units per hour is sent to block A, thus the total number of units sent to the block during the last two hours are: | ||
| Line 185: | Line 185: | ||
= & 4\times 2 \\ | = & 4\times 2 \\ | ||
= & 8\text{ }units | = & 8\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::The capacity of block A during these two hours is: | ::The capacity of block A during these two hours is: | ||
| Line 192: | Line 192: | ||
= & 15\times 2 \\ | = & 15\times 2 \\ | ||
= & 30\text{ }units | = & 30\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Thus, block A will process 8 units in the last two hours of phase P3 with an excess capacity of 22 units (30-8=22 units). | ::Thus, block A will process 8 units in the last two hours of phase P3 with an excess capacity of 22 units (30-8=22 units). | ||
| Line 202: | Line 202: | ||
= & 5\times 8 \\ | = & 5\times 8 \\ | ||
= & 40\text{ }units | = & 40\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::As a result, blocks B, C and D each process 37.33 units in the first eight hour of phase P3 with an excess capacity of 2.67 units (40-37.33=2.67 units). In the last two hours of the phase, block A sends a total of 8 units, with each block getting 2.67 units. The capacity of blocks B, C or D during these two hours is: | ::As a result, blocks B, C and D each process 37.33 units in the first eight hour of phase P3 with an excess capacity of 2.67 units (40-37.33=2.67 units). In the last two hours of the phase, block A sends a total of 8 units, with each block getting 2.67 units. The capacity of blocks B, C or D during these two hours is: | ||
| Line 209: | Line 209: | ||
= & 5\times 2 \\ | = & 5\times 2 \\ | ||
= & 10\text{ }units | = & 10\text{ }units | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::Thus, blocks B, C and D each process 2.67 units in the last two hours of phase P3 with an excess capacity of 7.33 units (10-2.67=7.33 units). At the end of these two hours phase P3 gets completed. This also marks the end of the simulation. | ::Thus, blocks B, C and D each process 2.67 units in the last two hours of phase P3 with an excess capacity of 7.33 units (10-2.67=7.33 units). At the end of these two hours phase P3 gets completed. This also marks the end of the simulation. | ||
| Line 215: | Line 215: | ||
::A summary result table for phase P3 is shown next. | ::A summary result table for phase P3 is shown next. | ||
[[Image:11t14.png|center| | [[Image:11t14.png|center|800px|link=]] | ||
A summary result table for the overall system for the simulation from 0 to 30 hrs is shown in the following table. | A summary result table for the overall system for the simulation from 0 to 30 hrs is shown in the following table. | ||
[[Image:11t15.png|center| | [[Image:11t15.png|center|800px|link=]] | ||
Latest revision as of 21:34, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.
This example appears in the System analysis reference.
To examine variable throughput in phase diagrams, consider a phase diagram of three phases with linked RBDs, as shown in the figure below. Each phase has a duration of 10 hours and all phases are set to continue simulation upon failure. Blocks A through E process a number of items per hour as identified next to each letter (e.g., A:10 implies that 10 units are processed per hour by block A). For the first phase, P1, the variable throughput model used is [math]\displaystyle{ y = x\,\! }[/math] (which is the linear model [math]\displaystyle{ y = ax+ b\,\! }[/math] with parameters [math]\displaystyle{ a = 1\,\! }[/math] and [math]\displaystyle{ b = 0\,\! }[/math]). For the second phase, P2, the model used is [math]\displaystyle{ y = 3x\,\! }[/math] (which is the linear model [math]\displaystyle{ y = ax+ b\,\! }[/math] with parameters [math]\displaystyle{ a = 3\,\! }[/math] and [math]\displaystyle{ b = 0\,\! }[/math]). The third phase uses [math]\displaystyle{ y = 0.5x\,\! }[/math] as the variable throughput model (which is the linear model [math]\displaystyle{ y = ax + b\,\! }[/math] with parameters [math]\displaystyle{ a = 0.5\,\! }[/math] and [math]\displaystyle{ b = 0\,\! }[/math]). Phases P1 and P2 have a value of 500 units per hour set for the maximum throughput capacity. This relatively larger value of throughput is set for the two phases so that the phases do not reach their maximum throughput value during the simulation. Phase P3 has a value of 4 units per hour set as the maximum throughput capacity. For the sake of simplicity it is assumed that the blocks can never fail and that items are routed equally to each path. The ignore backlog option is left unchecked for all blocks in the phase diagram.
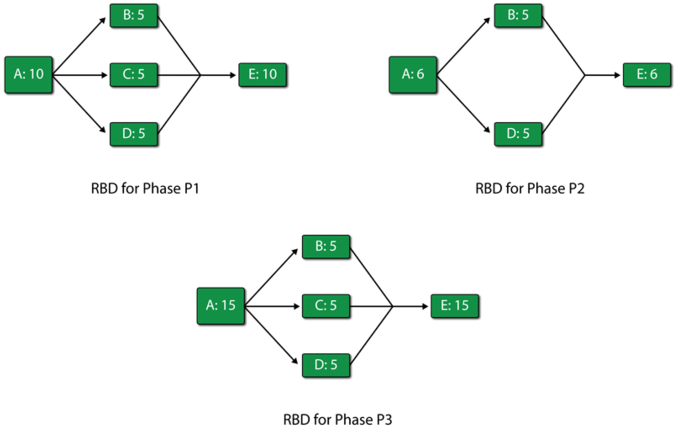
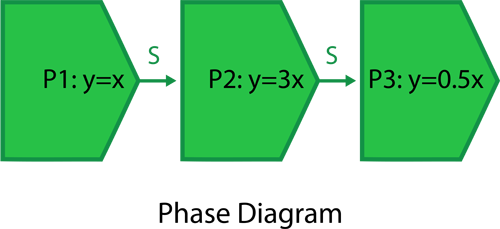
If a throughput simulation with an end time of 60 hours is run on the phase diagram, the following scenario can be observed:
- 1. Phase P1 from 0 to 10 hours
- a) The throughput from phase P1 follows a time-varying model given by [math]\displaystyle{ y = ax + b\,\! }[/math] with parameters [math]\displaystyle{ a = 1\,\! }[/math] and [math]\displaystyle{ b = 0\,\! }[/math]. Thus, during the first hour the throughput sent by phase P1 to block A is:
- [math]\displaystyle{ \begin{align} Phase throughput from 0 to 1hr= & \frac{a}{2}(x_{2}^{2}-x_{1}^{2})+b({{x}_{2}}-{{x}_{1}}) \\ = & \frac{1}{2}({{1}^{2}}-{{0}^{2}})+0(1-0) \\ = & 0.5\text{ }units \end{align}\,\! }[/math]
- And the throughput sent by phase P1 to block A in the second hour is:
- [math]\displaystyle{ \begin{align} Phase throughput from 1 to 2 hrs= & \frac{a}{2}(x_{2}^{2}-x_{1}^{2})+b({{x}_{2}}-{{x}_{1}}) \\ = & \frac{1}{2}({{2}^{2}}-{{1}^{2}})+0(2-1) \\ = & 1.5\text{ }units \end{align}\,\! }[/math]
- It can be seen that the throughput from phase P1 sent to block A increases with time. But the capacity of block A remains constant at 10 units per hour during the entire phase P1. Thus, it becomes important to know the point of time when the number of units sent by P1 exceed the capacity of block A and the block starts accumulating a backlog. This can be obtained by solving the throughput model for phase P1 [math]\displaystyle{ (y = x)\,\! }[/math] using the capacity of block A by substituting [math]\displaystyle{ y\,\! }[/math] as the block capacity as shown next:
- [math]\displaystyle{ \begin{align} y= & x \\ or\text{ }10= & x \end{align}\,\! }[/math]
- Thus, at time [math]\displaystyle{ x = 10\,\! }[/math] hours the number of units supplied per hour by phase P1 will equal the capacity of block A. At this point of time block A will function to its full capacity with no excess capacity and no backlog. Beyond this point the units sent by phase P1 will exceed the capacity of block A and the block will start accumulating a backlog. Since the duration of phase P1 is 10 hours, backlog at block A will not be a concern in this phase because up to this time the capacity of the block exceeds the units sent by phase P1. Thus, the total units sent by phase P1 to block A during the phase duration of 10 hours is:
- [math]\displaystyle{ \begin{align} = & \frac{a}{2}(x_{2}^{2}-x_{1}^{2})+b({{x}_{2}}-{{x}_{1}}) \\ = & \frac{1}{2}({{10}^{2}}-{{0}^{2}})+0(10-0) \\ = & 50\text{ }units \end{align}\,\! }[/math]
- The total number of units that can be processed by block A (or the capacity of A) during phase P1 is:
- [math]\displaystyle{ \begin{align} = & 10\times 10 \\ = & 100\text{ }units \end{align}\,\! }[/math]
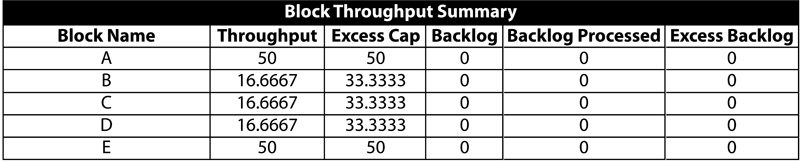
- Thus, during the first phase, block A processes all 50 units sent by phase P1 with an excess capacity of 50 units (100-50=50 units).
- b) The 50 units processed by block A from time 0 to 10 hours are routed equally over three paths to blocks B, C and D. Each of these blocks gets a total of 16.67 units from time 0 to 10 hours. The capacity of each of these blocks is 5 units per hour. Thus, the total capacity of each of the blocks from time 0 to 10 hours is 50 units. As a result, each of the three blocks processes 16.67 units in phase P1 with an excess capacity of 33.33 units.
- c) Blocks B, C and D route each of their 16.67 units to block E. The capacity of E in this phase is 10 units per hour or 100 units for the ten hours. Thus, block E processes a total of 50 units from blocks B, C and D with an excess capacity of 50 units during the first phase P1. At 10 hours, phase P1 ends and phase P2 begins.
- A summary result table for phase P1 is shown next.
- 2. Phase P2 from 10 to 20 hours
- a) The throughput of phase P2 follows the model [math]\displaystyle{ y = ax + b\,\! }[/math] with [math]\displaystyle{ a = 3\,\! }[/math] and [math]\displaystyle{ b = 0\,\! }[/math]. The throughput from P2 goes to block A. The capacity of block A in this phase is 6 units per hour. The point of time when the number of units sent by P2 equals the capacity of block A can be obtained by substituting the capacity of block A into the model equation [math]\displaystyle{ (y = 3x)\,\! }[/math] as shown next:
- [math]\displaystyle{ \begin{align} y= & 3x \\ or\text{ }6= & 3x \\ or\text{ }x= & 2 \end{align}\,\! }[/math]
- Thus, at [math]\displaystyle{ x = 2\,\! }[/math] hours of phase P2 (or at the total simulation time of 12 hours), the number of units sent per hour by phase P2 equals the capacity of block A. Thus, during the first two hours of phase P2, block A will have excess capacity. The total number of units sent by phase P2 during the first two hours of the phase is:
- [math]\displaystyle{ \begin{align} = & \frac{a}{2}(x_{2}^{2}-x_{1}^{2})+b({{x}_{2}}-{{x}_{1}}) \\ = & \frac{3}{2}({{2}^{2}}-{{0}^{2}})+0(2-0) \\ = & 6\text{ }units \end{align}\,\! }[/math]
- The total capacity of block A during the first two hours of phase P2 is:
- [math]\displaystyle{ \begin{align} = & 6\times 2 \\ = & 12\text{ }units \end{align}\,\! }[/math]
- Thus block A processes a total of 6 units in the first two hours of phase P2 with an excess capacity of 6 units (12-6=6 units). During the last eight hours of the phase (from the second hour to the tenth hour) block A will have a backlog because the number of units sent by phase P2 will exceed block A's capacity. The total number of units sent by phase P2 during the last eight hours of the phase is:
- [math]\displaystyle{ \begin{align} = & \frac{a}{2}(x_{2}^{2}-x_{1}^{2})+b({{x}_{2}}-{{x}_{1}}) \\ = & \frac{3}{2}({{10}^{2}}-{{2}^{2}})+0(10-2) \\ = & 144\text{ }units \end{align}\,\! }[/math]
- The total capacity of block A during these eight hours of phase P2 is:
- [math]\displaystyle{ \begin{align} = & 6\times 8 \\ = & 48\text{ }units \end{align}\,\! }[/math]
- Thus, during the last eight hours of phase P2, block A will process a total of 48 units with a backlog of 96 units (144-48=96 units). A graphical representation of the above scenario for block A during phase P2 is shown in the figure below.
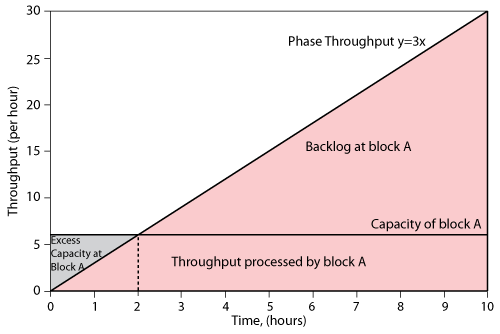
- b) The units processed by block A are routed equally to blocks B and D, as block C is absent in this phase. During the first two hours, block A sends a total of 6 units that are divided equally among blocks B and D, with each block getting 3 units. The capacity of these blocks in this phase is 5 units per hour. Thus the total capacity of each of these blocks during the first two hours of phase P2 is:
- [math]\displaystyle{ \begin{align} = & 5\times 2 \\ = & 10\text{ }units \end{align}\,\! }[/math]
- As a result, blocks B and D each process 3 units in the first two hours of phase P2 with an excess capacity of 7 units (10-3=7 units). During the last eight hours of phase P2, block A sends a total of 48 units to blocks B and D, with each block receiving 24 units. The capacity of each of these blocks during these eight hours is:
- [math]\displaystyle{ \begin{align} = & 5\times 8 \\ = & 40\text{ }units \end{align}\,\! }[/math]
- Thus, B and D process 24 units in the last eight hours of phase P2, with an excess capacity of 16 units (40-24=16 units).
- c) The units processed by blocks B and D are sent to block E. The capacity of E in this phase is 6 units per hour. During the first two hours of phase P2, a total of 6 units are sent to block E. The total capacity of block E during this period of time is:
- [math]\displaystyle{ \begin{align} = & 6\times 2 \\ = & 12\text{ }units \end{align}\,\! }[/math]
- Consequently block E processes 6 units in the first two hours of phase P2 with an excess capacity of 6 units (12-6=6 units). During the last eight hours of the phase, blocks B and D send a total of 48 units to block E. The capacity of block E during this time is:
- [math]\displaystyle{ \begin{align} = & 6\times 8 \\ = & 48\text{ }units \end{align}\,\! }[/math]
- Thus, block E processes 48 units in the last eight hours of P2 with no excess capacity and no backlog. At 20 hrs phase P2 ends and phase P3 begins.
- A summary result table for phase P2 is shown next.

- 3. Phase P3 from 20 to 30 hours
- a) The throughput of phase P3 follows the model [math]\displaystyle{ y = ax + b\,\! }[/math] with [math]\displaystyle{ a = 0.5\,\! }[/math] and [math]\displaystyle{ b = 0\,\! }[/math]. A maximum throughput capacity of 4 units per hour is also set for this phase. The throughput from this phase goes to block A. The capacity of block A in this phase is 15 units per hour. Thus, it can be seen that the throughput sent by phase P3 will never exceed the capacity of block A in this phase. It can also be seen that at some point of time the throughput of phase P3 will reach the maximum throughput capacity of 4 units per hour and, thereafter, a constant throughput of 4 units per hour will be sent by phase P3. This point of time can be calculated by solving the linear throughput model for the phase [math]\displaystyle{ y = 0.5x\,\! }[/math] by substituting [math]\displaystyle{ y\,\! }[/math] as the maximum throughput capacity as shown next:
- [math]\displaystyle{ \begin{align} y= & 0.5x \\ or\text{ }4= & 0.5x \\ or\text{ }x= & 8 \end{align}\,\! }[/math]
- Thus, at time [math]\displaystyle{ x = 8\,\! }[/math] hours of phase P3 (or at the time of 28 hours) the number of units sent per hour by phase P3 will reach the constant value of 4 units per hour. In the first eight hours of the phase the throughput will remain variable. The total number of units sent by P3 to block A during this time is given by:
- [math]\displaystyle{ \begin{align} = & \frac{a}{2}(x_{2}^{2}-x_{1}^{2})+b({{x}_{2}}-{{x}_{1}}) \\ = & \frac{0.5}{2}({{8}^{2}}-{{0}^{2}})+0(8-0) \\ = & 16\text{ }units \end{align}\,\! }[/math]
- The total capacity of block A during the first eight hours of phase P3 is:
- [math]\displaystyle{ \begin{align} = & 15\times 8 \\ = & 120\text{ }units \end{align}\,\! }[/math]
- Consequently, it can be seen that block A has an excess capacity of 104 units (120-16=104 units). Thus, block A will be able to process all of the 96 units of backlog from phase P2 during these eight hours. As a result, block A will process a total of 112 units (16 units from P3 and 96 units from the backlog of phase P2) with an excess capacity of 8 units (120-112=8 units) during the first eight hours of phase P3. In the last two hours of this phase, a constant throughput of 4 units per hour is sent to block A, thus the total number of units sent to the block during the last two hours are:
- [math]\displaystyle{ \begin{align} = & 4\times 2 \\ = & 8\text{ }units \end{align}\,\! }[/math]
- The capacity of block A during these two hours is:
- [math]\displaystyle{ \begin{align} = & 15\times 2 \\ = & 30\text{ }units \end{align}\,\! }[/math]
- Thus, block A will process 8 units in the last two hours of phase P3 with an excess capacity of 22 units (30-8=22 units).
- b) The units processed by block A are routed equally over three paths to blocks B, C and D, as block C is available again in this phase. During the first eight hours of phase P3 a total of 112 units are sent to blocks B, C and D, with each block receiving 37.33 units. The capacity of each of these block is 5 units per hour, thus the total capacity of each of the blocks during the first eight hours is:
- [math]\displaystyle{ \begin{align} = & 5\times 8 \\ = & 40\text{ }units \end{align}\,\! }[/math]
- As a result, blocks B, C and D each process 37.33 units in the first eight hour of phase P3 with an excess capacity of 2.67 units (40-37.33=2.67 units). In the last two hours of the phase, block A sends a total of 8 units, with each block getting 2.67 units. The capacity of blocks B, C or D during these two hours is:
- [math]\displaystyle{ \begin{align} = & 5\times 2 \\ = & 10\text{ }units \end{align}\,\! }[/math]
- Thus, blocks B, C and D each process 2.67 units in the last two hours of phase P3 with an excess capacity of 7.33 units (10-2.67=7.33 units). At the end of these two hours phase P3 gets completed. This also marks the end of the simulation.
- A summary result table for phase P3 is shown next.
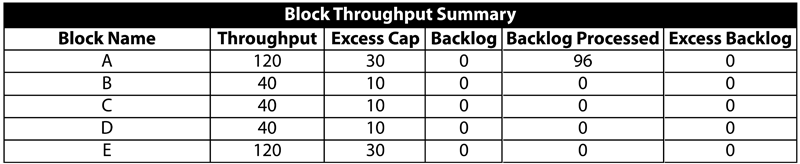
A summary result table for the overall system for the simulation from 0 to 30 hrs is shown in the following table.