Reliability Data - Modified Gompertz Model: Difference between revisions
No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner RGA Examples}} | <noinclude>{{Banner RGA Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis Reliability growth reference]''. | ||
</noinclude> | </noinclude> | ||
| Line 31: | Line 31: | ||
|8|| 99.00|| 92.76|| 99.10|| 99.27 | |8|| 99.00|| 92.76|| 99.10|| 99.27 | ||
|} | |} | ||
'''Solution''' | '''Solution''' | ||
| Line 37: | Line 36: | ||
To determine the parameters of the modified Gompertz curve, use: | To determine the parameters of the modified Gompertz curve, use: | ||
:<math>\begin{align} | |||
& {{S}_{1}}(d)= & \underset{i=0}{\overset{2}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ | & {{S}_{1}}(d)= & \underset{i=0}{\overset{2}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ | ||
& {{S}_{2}}(d)= & \underset{i=3}{\overset{5}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ | & {{S}_{2}}(d)= & \underset{i=3}{\overset{5}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ | ||
Latest revision as of 21:31, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability growth reference.
A reliability growth data set is given in columns 1 and 2 of the following table. Find the modified Gompertz curve that represents the data and plot it comparatively with the raw data.
| Time(months) | Raw Data Reliability(%) | Gompertz Reliability(%) | Logistic Reliability(%) | Modified Gompertz Reliability(%) |
|---|---|---|---|---|
| 0 | 31.00 | 25.17 | 22.70 | 31.18 |
| 1 | 35.50 | 38.33 | 38.10 | 35.08 |
| 2 | 49.30 | 51.35 | 56.40 | 49.92 |
| 3 | 70.10 | 62.92 | 73.00 | 69.23 |
| 4 | 83.00 | 72.47 | 85.00 | 83.72 |
| 5 | 92.20 | 79.94 | 93.20 | 92.06 |
| 6 | 96.40 | 85.59 | 96.10 | 96.29 |
| 7 | 98.60 | 89.75 | 98.10 | 98.32 |
| 8 | 99.00 | 92.76 | 99.10 | 99.27 |
Solution
To determine the parameters of the modified Gompertz curve, use:
- [math]\displaystyle{ \begin{align} & {{S}_{1}}(d)= & \underset{i=0}{\overset{2}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ & {{S}_{2}}(d)= & \underset{i=3}{\overset{5}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \\ & {{S}_{3}}(d)= & \underset{i=6}{\overset{8}{\mathop \sum }}\,\ln ({{R}_{oi}}-d) \end{align}\,\! }[/math]
- [math]\displaystyle{ c(d)={{\left[ \frac{{{S}_{3}}(d)-{{S}_{2}}(d)}{{{S}_{2}}(d)-{{S}_{1}}(d)} \right]}^{\tfrac{1}{3}}}\,\! }[/math]
- [math]\displaystyle{ a(d)={{e}^{\left[ \tfrac{1}{3}\left( {{S}_{1}}(d)+\tfrac{{{S}_{2}}(d)-{{S}_{1}}(d)}{1-{{[c(d)]}^{3}}} \right) \right]}}\,\! }[/math]
- [math]\displaystyle{ b(d)={{e}^{\left[ \tfrac{({{S}_{2}}(d)-{{S}_{1}}(d))(c(d)-1)}{{{\left[ 1-{{[c(d)]}^{3}} \right]}^{2}}} \right]}}\,\! }[/math]
and:
- [math]\displaystyle{ {{R}_{0}}=d+a(d)\cdot b(d)\,\! }[/math]
for [math]\displaystyle{ {{R}_{0}}=31%\,\! }[/math], the equation above may be rewritten as:
- [math]\displaystyle{ d-31+a(d)\cdot b(d)=0\,\! }[/math]
The equations for parameters [math]\displaystyle{ c\,\! }[/math], [math]\displaystyle{ a\,\! }[/math] and [math]\displaystyle{ b\,\! }[/math] can now be solved simultaneously. One method for solving these equations numerically is to substitute different values of [math]\displaystyle{ d\,\! }[/math], which must be less than [math]\displaystyle{ {{R}_{0}}\,\! }[/math], into the last equation shown above, and plot the results along the y-axis with the value of [math]\displaystyle{ d\,\! }[/math] along the x-axis. The value of [math]\displaystyle{ d\,\! }[/math] can then be read from the x-intercept. This can be repeated for greater accuracy using smaller and smaller increments of [math]\displaystyle{ d\,\! }[/math]. Once the desired accuracy on [math]\displaystyle{ d\,\! }[/math] has been achieved, the value of [math]\displaystyle{ d\,\! }[/math] can then be used to solve for [math]\displaystyle{ a\,\! }[/math], [math]\displaystyle{ b\,\! }[/math] and [math]\displaystyle{ c\,\! }[/math]. For this case, the initial estimates of the parameters are:
- [math]\displaystyle{ \begin{align} \widehat{a}= & 69.324 \\ \widehat{b}= & 0.002524 \\ \widehat{c}= & 0.46012 \\ \widehat{d}= & 30.825 \end{align}\,\! }[/math]
Now, since the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting [math]\displaystyle{ {{Y}_{i}}={{R}_{i}},\,\! }[/math] [math]\displaystyle{ g_{1}^{(0)}=69.324,\,\! }[/math] [math]\displaystyle{ g_{2}^{(0)}=0.002524,\,\! }[/math] [math]\displaystyle{ g_{3}^{(0)}=0.46012,\,\! }[/math] and [math]\displaystyle{ g_{4}^{(0)}=30.825\,\! }[/math], [math]\displaystyle{ {{Y}^{(0)}},{{D}^{(0)}},\,\! }[/math] [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] become:
- [math]\displaystyle{ {{Y}^{(0)}}=\left[ \begin{matrix} 0.000026 \\ 0.253873 \\ -1.062940 \\ 0.565690 \\ -0.845260 \\ 0.096737 \\ 0.076450 \\ 0.238155 \\ -0.320890 \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ {{D}^{(0)}}=\left[ \begin{matrix} 0.002524 & 69.3240 & 0.0000 & 1 \\ 0.063775 & 805.962 & -26.4468 & 1 \\ 0.281835 & 1638.82 & -107.552 & 1 \\ 0.558383 & 1493.96 & -147.068 & 1 \\ 0.764818 & 941.536 & -123.582 & 1 \\ 0.883940 & 500.694 & -82.1487 & 1 \\ 0.944818 & 246.246 & -48.4818 & 1 \\ 0.974220 & 116.829 & -26.8352 & 1 \\ 0.988055 & 54.5185 & -14.3117 & 1 \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ {{\nu }^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ g_{4}^{(0)} \\ \end{matrix} \right]=\left[ \begin{matrix} 69.324 \\ 0.002524 \\ 0.46012 \\ 30.825 \\ \end{matrix} \right]\,\! }[/math]
The estimate of the parameters [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] is given by:
- [math]\displaystyle{ \begin{align} {{\widehat{\nu }}^{(0)}}= & {{\left( {{D}^{{{(0)}^{T}}}}{{D}^{(0)}} \right)}^{-1}}{{D}^{{{(0)}^{T}}}}{{Y}^{(0)}} \\ = & \left[ \begin{matrix} -0.275569 \\ -0.000549 \\ -0.003202 \\ 0.209458 \\ \end{matrix} \right] \end{align}\,\! }[/math]
The revised estimated regression coefficients in matrix form are given by:
- [math]\displaystyle{ \begin{align} {{g}^{(1)}}= & {{g}^{(0)}}+{{\widehat{\nu }}^{(0)}}. \\ = & \left[ \begin{matrix} 69.324 \\ 0.002524 \\ 0.46012 \\ 30.825 \\ \end{matrix} \right]+\left[ \begin{matrix} -0.275569 \\ -0.000549 \\ -0.003202 \\ 0.209458 \\ \end{matrix} \right] \\ = & \left[ \begin{matrix} 69.0484 \\ 0.00198 \\ 0.45692 \\ 31.0345 \\ \end{matrix} \right] \end{align}\,\! }[/math]
With the starting coefficients [math]\displaystyle{ {{g}^{(0)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} {{Q}^{(0)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left( {{Y}_{i}}-f({{T}_{i}},{{g}^{(0)}}) \right)}^{2}} \\ = & 2.403672 \end{align}\,\! }[/math]
With the coefficients at the end of the first iteration, [math]\displaystyle{ {{g}^{(1)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} {{Q}^{(1)}}= & \underset{i=1}{\overset{N}{\mathop \sum }}\,{{\left[ {{Y}_{i}}-f\left( {{T}_{i}},{{g}^{(1)}} \right) \right]}^{2}} \\ = & 2.073964 \end{align}\,\! }[/math]
Therefore:
- [math]\displaystyle{ \begin{align} {{Q}^{(1)}}\lt {{Q}^{(0)}} \end{align}\,\! }[/math]
Hence, the Gauss-Newton method works in the right direction. The iterations are continued until the relationship of [math]\displaystyle{ {{Q}^{(s-1)}}-{{Q}^{(s)}}\simeq 0\,\! }[/math] has been satisfied. Using RGA, the estimators of the parameters are:
- [math]\displaystyle{ \begin{align} \widehat{a}= & 0.6904 \\ \widehat{b}= & 0.0020 \\ \widehat{c}= & 0.4567 \\ \widehat{d}= & 0.3104 \end{align}\,\! }[/math]
Therefore, the modified Gompertz model is:
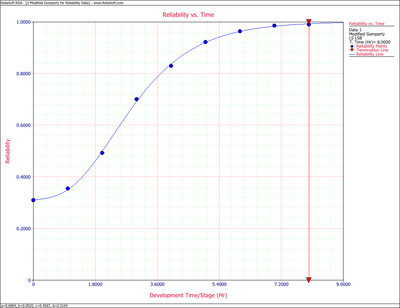
- [math]\displaystyle{ R=0.3104+(0.6904){{(0.0020)}^{{{0.4567}^{T}}}}\,\! }[/math]
Using this equation, the predicted reliability is plotted in the following figure along with the raw data. As you can see, the modified Gompertz curve represents the data very well.