Reliability Data - Standard Gompertz Model: Difference between revisions
Kate Racaza (talk | contribs) (Created page with '<noinclude>{{Banner RGA Examples}} ''This example appears in the Reliability Growth and Repairable System Analysis Reference book''. </noinclude> A device is…') |
Lisa Hacker (talk | contribs) No edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner RGA Examples}} | <noinclude>{{Banner RGA Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis Reliability growth reference]''. | ||
</noinclude> | </noinclude> | ||
A device is required to have a reliability of 92% at the end of a 12-month design and development period. The following table gives the data obtained for the first five moths. | A device is required to have a reliability of 92% at the end of a 12-month design and development period. The following table gives the data obtained for the first five moths. | ||
<ol> | |||
<li>What will the reliability be at the end of this 12-month period?</li> | |||
<li>What will the maximum achievable reliability be if the reliability program plan pursued during the first 5 months is continued?</li> | |||
<li>How do the predicted reliability values compare with the actual values? | |||
</ol> | |||
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | ||
|+'''Design and Development Time vs. Demonstrated Reliability Data for a Device''' | |+'''Design and Development Time vs. Demonstrated Reliability Data for a Device''' | ||
| Line 37: | Line 37: | ||
'''Solution''' | '''Solution''' | ||
After generating the table above and calculating the last column to find <math>{{S}_{1}}\,\!</math>, <math>{{S}_{2}}\,\!</math> and <math>{{S}_{3}}\,\!</math>, proceed as follows: | |||
: | <ol style="list-style-type: lower-alpha;"> | ||
<li>Solve for the value of <math>c\,\!</math>: | |||
:<math>\begin{align} | |||
c= & {{\left( \frac{8.850-8.641}{8.641-8.250} \right)}^{\tfrac{1}{2}}} \\ | c= & {{\left( \frac{8.850-8.641}{8.641-8.250} \right)}^{\tfrac{1}{2}}} \\ | ||
= & 0.731 | = & 0.731 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
</li> | |||
<li>Solve for the value of <math>a\,\!</math>: | |||
:<math>\begin{align} | |||
a&=e^\left[({\frac{1}{2}\left ( 8.250+\frac{S_{2}-S_{1}}{1-c^{n\cdot 1}} \right )} \right ] \\ | a&=e^\left[({\frac{1}{2}\left ( 8.250+\frac{S_{2}-S_{1}}{1-c^{n\cdot 1}} \right )} \right ] \\ | ||
&=e^{4.545} \\ | &=e^{4.545} \\ | ||
| Line 55: | Line 56: | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
:This is the upper limit for the reliability as <math>T\to \infty \,\!</math>. | |||
</li> | |||
<li>Solve for the value of <math>b\,\!</math>: | |||
:<math>\begin{align} | |||
b= & {{e}^{\left[ \tfrac{(8.641-8.250)(0.731-1)}{{{(1-{{0.731}^{2}})}^{2}}} \right]}} \\ | b= & {{e}^{\left[ \tfrac{(8.641-8.250)(0.731-1)}{{{(1-{{0.731}^{2}})}^{2}}} \right]}} \\ | ||
= & {{e}^{(-0.485)}} \\ | = & {{e}^{(-0.485)}} \\ | ||
= & 0.615 | = & 0.615 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
</li> | |||
</ol> | |||
Now, that the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting <math>{{Y}_{i}}={{R}_{i}},\,\!</math> <math>g_{1}^{(0)}=94.16,\,\!</math> <math>g_{2}^{(0)}=0.615,\,\!</math> <math>g_{3}^{(0)}=0.731,\,\!</math> <math>{{Y}^{(0)}},{{D}^{(0)}},\,\!</math> <math>{{\nu }^{(0)}}\,\!</math> become: | Now, that the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting <math>{{Y}_{i}}={{R}_{i}},\,\!</math> <math>g_{1}^{(0)}=94.16,\,\!</math> <math>g_{2}^{(0)}=0.615,\,\!</math> <math>g_{3}^{(0)}=0.731,\,\!</math> <math>{{Y}^{(0)}},{{D}^{(0)}},\,\!</math> <math>{{\nu }^{(0)}}\,\!</math> become: | ||
:<math>{{Y}^{(0)}}=\left[ \begin{matrix} | |||
0.0916 \\ | 0.0916 \\ | ||
0.0015 \\ | 0.0015 \\ | ||
| Line 77: | Line 78: | ||
-0.0743 \\ | -0.0743 \\ | ||
\end{matrix} \right]\,\!</math> | \end{matrix} \right]\,\!</math> | ||
:<math>{{D}^{(0)}}=\left[ \begin{matrix} | |||
0.6150 & 94.1600 & 0.0000 \\ | 0.6150 & 94.1600 & 0.0000 \\ | ||
0.7009 & 78.4470 & -32.0841 \\ | 0.7009 & 78.4470 & -32.0841 \\ | ||
| Line 85: | Line 86: | ||
0.9035 & 28.8742 & -59.0463 \\ | 0.9035 & 28.8742 & -59.0463 \\ | ||
\end{matrix} \right]\,\!</math> | \end{matrix} \right]\,\!</math> | ||
:<math>{{\nu }^{(0)}}=\left[ \begin{matrix} | |||
g_{1}^{(0)} \\ | g_{1}^{(0)} \\ | ||
g_{2}^{(0)} \\ | g_{2}^{(0)} \\ | ||
| Line 94: | Line 95: | ||
0.731 \\ | 0.731 \\ | ||
\end{matrix} \right]\,\!</math> | \end{matrix} \right]\,\!</math> | ||
The estimate of the parameters <math>{{\nu }^{(0)}}\,\!</math> is given by: | The estimate of the parameters <math>{{\nu }^{(0)}}\,\!</math> is given by: | ||
:<math>\begin{align} | |||
\hat{v}&=\left ( D^{(0)}D^{(0)} \right )^{-1}D^{(0)}Y^{(0)} \\ | \hat{v}&=\left ( D^{(0)}D^{(0)} \right )^{-1}D^{(0)}Y^{(0)} \\ | ||
&=\begin{bmatrix}0.061575\\ 0.000222\\ 0.001123\end{bmatrix} | &=\begin{bmatrix}0.061575\\ 0.000222\\ 0.001123\end{bmatrix} | ||
\end{align}</math> | \end{align}</math> | ||
The revised estimated regression coefficients in matrix form are: | The revised estimated regression coefficients in matrix form are: | ||
:<math>\begin{align} | |||
g^{(1)}&=g^{(0)} + \hat{v}^{(0)} \\ | g^{(1)}&=g^{(0)} + \hat{v}^{(0)} \\ | ||
&= \begin{bmatrix}94.16\\ 0.615\\ 0.731\end{bmatrix}+\begin{bmatrix}0.061575\\ 0.000222\\ 0.001123\end{bmatrix} \\ | &= \begin{bmatrix}94.16\\ 0.615\\ 0.731\end{bmatrix}+\begin{bmatrix}0.061575\\ 0.000222\\ 0.001123\end{bmatrix} \\ | ||
&=\begin{bmatrix}94.2216\\ 0.6152\\ 0.7321\end{bmatrix} | &=\begin{bmatrix}94.2216\\ 0.6152\\ 0.7321\end{bmatrix} | ||
\end{align}</math> | \end{align}</math> | ||
If the Gauss-Newton method works effectively, then the relationship <math>{{Q}^{(k+1)}}<{{Q}^{(k)}}\,\! </math> has to hold, meaning that <math>{{g}^{(k+1)}}\,\!</math> gives better estimates than <math>{{g}^{(k)}}\,\!</math>, after <math>k\,\!</math>. With the starting coefficients, <math>{{g}^{(0)}}\,\!</math>, <math>Q\,\!</math> is: | If the Gauss-Newton method works effectively, then the relationship <math>{{Q}^{(k+1)}}<{{Q}^{(k)}}\,\! </math> has to hold, meaning that <math>{{g}^{(k+1)}}\,\!</math> gives better estimates than <math>{{g}^{(k)}}\,\!</math>, after <math>k\,\!</math>. With the starting coefficients, <math>{{g}^{(0)}}\,\!</math>, <math>Q\,\!</math> is: | ||
:<math>\begin{align} | |||
Q^{0}&=\sum_{i=1}^{N}\left [ Y_{i}-f\left ( T_{i}, g^{(0)} \right ) \right ]^{2}\\ | Q^{0}&=\sum_{i=1}^{N}\left [ Y_{i}-f\left ( T_{i}, g^{(0)} \right ) \right ]^{2}\\ | ||
&= 0.045622 | &= 0.045622 | ||
\end{align}</math> | \end{align}</math> | ||
And with the coefficients at the end of the first iteration, <math>{{g}^{(1)}}\,\!</math>, <math>Q\,\!</math> is: | And with the coefficients at the end of the first iteration, <math>{{g}^{(1)}}\,\!</math>, <math>Q\,\!</math> is: | ||
:<math>\begin{align} | |||
Q^{1}&=\sum_{i=1}^{N}\left [ Y_{i}-f\left ( T_{i}, g^{(1)} \right ) \right ]^{2}\\ | Q^{1}&=\sum_{i=1}^{N}\left [ Y_{i}-f\left ( T_{i}, g^{(1)} \right ) \right ]^{2}\\ | ||
&= 0.041439 | &= 0.041439 | ||
\end{align}</math> | \end{align}</math> | ||
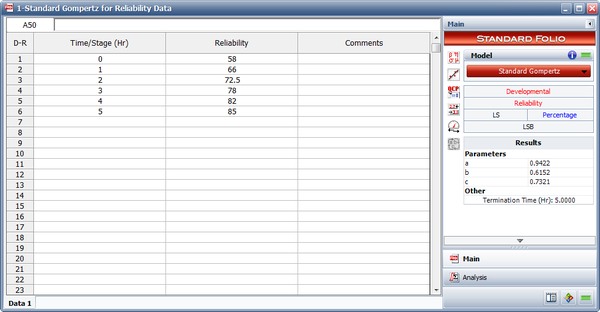
Therefore, it can be justified that the Gauss-Newton method works in the right direction. The iterations are continued until the relationship <math>Q^{(s-1)}-Q^{(s)}\simeq 0</math> is satisfied. Note that the RGA software uses a different analysis method called the ''Levenberg-Marquardt''. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods. The estimated parameters using RGA are shown in the figure below. | Therefore, it can be justified that the Gauss-Newton method works in the right direction. The iterations are continued until the relationship <math>Q^{(s-1)}-Q^{(s)}\simeq 0</math> is satisfied. Note that the RGA software uses a different analysis method called the ''Levenberg-Marquardt''. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods. The estimated parameters using RGA are shown in the figure below. | ||
[[Image:rga7.2.png | [[Image:rga7.2.png|center|600px]] | ||
They are: | They are: | ||
:<math>\begin{align} | |||
& \widehat{a}= & 0.9422 \\ | & \widehat{a}= & 0.9422 \\ | ||
& \widehat{b}= & 0.6152 \\ | & \widehat{b}= & 0.6152 \\ | ||
& \widehat{c}= & 0.7321 | & \widehat{c}= & 0.7321 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
The Gompertz reliability growth curve is: | The Gompertz reliability growth curve is: | ||
:<math>R=0.9422{{(0.6152)}^{{{0.7321}^{T}}}}\,\!</math> | |||
<ol> | |||
<li>The achievable reliability at the end of the 12-month period of design and development is: | |||
:<math>\begin{align} | |||
R&=0.9422(0.6152)^{0.7321} | R&=0.9422(0.6152)^{0.7321} | ||
&=0.9314 | &=0.9314 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
The required reliability is 92%. Consequently, from the previous result, this requirement will be barely met. Every effort should therefore be expended to implement the reliability program plan fully, and perhaps augment it slightly to assure that the reliability goal will be met. | The required reliability is 92%. Consequently, from the previous result, this requirement will be barely met. Every effort should therefore be expended to implement the reliability program plan fully, and perhaps augment it slightly to assure that the reliability goal will be met. | ||
</li><li>The maximum achievable reliability from Step 2, or from the value of <math>a\,\!</math>, is 0.9422. | |||
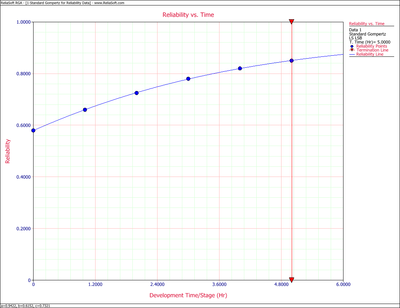
</li><li>The predicted reliability values, as calculated from the standard Gompertz model, are compared with the actual data in the table below. It may be seen in the table that the Gompertz curve appears to provide a very good fit for the data used because the equation reproduces the available data with less than 1% error. The standard Gompertz model is plotted in the figure below the table. The plot identifies the type of reliability growth curve that the equation represents. | |||
| Line 193: | Line 188: | ||
|12|| 93.14|| | |12|| 93.14|| | ||
|} | |} | ||
[[Image:rga7.3.png|center|400px|Plot of the reliability growth curve]] | [[Image:rga7.3.png|center|400px|Plot of the reliability growth curve]] | ||
</li> | |||
</ol> | |||
Latest revision as of 21:31, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability growth reference.
A device is required to have a reliability of 92% at the end of a 12-month design and development period. The following table gives the data obtained for the first five moths.
- What will the reliability be at the end of this 12-month period?
- What will the maximum achievable reliability be if the reliability program plan pursued during the first 5 months is continued?
- How do the predicted reliability values compare with the actual values?
| Group Number | Growth Time [math]\displaystyle{ T\,\! }[/math](months) | Reliability [math]\displaystyle{ R\,\! }[/math](%) | [math]\displaystyle{ \ln{R}\,\! }[/math] |
|---|---|---|---|
| 0 | 58 | 4.060 | |
| 1 | 1 | 66 | 4.190 |
| [math]\displaystyle{ {{S}_{1}}\,\! }[/math] = 8.250 | |||
| 2 | 72.5 | 4.284 | |
| 2 | 3 | 78 | 4.357 |
| [math]\displaystyle{ {{S}_{2}}\,\! }[/math] = 8.641 | |||
| 4 | 82 | 4.407 | |
| 3 | 5 | 85 | 4.443 |
| [math]\displaystyle{ {{S}_{3}}\,\! }[/math] = 8.850 |
Solution
After generating the table above and calculating the last column to find [math]\displaystyle{ {{S}_{1}}\,\! }[/math], [math]\displaystyle{ {{S}_{2}}\,\! }[/math] and [math]\displaystyle{ {{S}_{3}}\,\! }[/math], proceed as follows:
- Solve for the value of [math]\displaystyle{ c\,\! }[/math]:
- [math]\displaystyle{ \begin{align} c= & {{\left( \frac{8.850-8.641}{8.641-8.250} \right)}^{\tfrac{1}{2}}} \\ = & 0.731 \end{align}\,\! }[/math]
- Solve for the value of [math]\displaystyle{ a\,\! }[/math]:
- [math]\displaystyle{ \begin{align} a&=e^\left[({\frac{1}{2}\left ( 8.250+\frac{S_{2}-S_{1}}{1-c^{n\cdot 1}} \right )} \right ] \\ &=e^{4.545} \\ &=94.16% \end{align}\,\! }[/math]
- This is the upper limit for the reliability as [math]\displaystyle{ T\to \infty \,\! }[/math].
- Solve for the value of [math]\displaystyle{ b\,\! }[/math]:
- [math]\displaystyle{ \begin{align} b= & {{e}^{\left[ \tfrac{(8.641-8.250)(0.731-1)}{{{(1-{{0.731}^{2}})}^{2}}} \right]}} \\ = & {{e}^{(-0.485)}} \\ = & 0.615 \end{align}\,\! }[/math]
Now, that the initial values have been determined, the Gauss-Newton method can be used. Therefore, substituting [math]\displaystyle{ {{Y}_{i}}={{R}_{i}},\,\! }[/math] [math]\displaystyle{ g_{1}^{(0)}=94.16,\,\! }[/math] [math]\displaystyle{ g_{2}^{(0)}=0.615,\,\! }[/math] [math]\displaystyle{ g_{3}^{(0)}=0.731,\,\! }[/math] [math]\displaystyle{ {{Y}^{(0)}},{{D}^{(0)}},\,\! }[/math] [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] become:
- [math]\displaystyle{ {{Y}^{(0)}}=\left[ \begin{matrix} 0.0916 \\ 0.0015 \\ -0.1190 \\ 0.1250 \\ 0.0439 \\ -0.0743 \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ {{D}^{(0)}}=\left[ \begin{matrix} 0.6150 & 94.1600 & 0.0000 \\ 0.7009 & 78.4470 & -32.0841 \\ 0.7712 & 63.0971 & -51.6122 \\ 0.8270 & 49.4623 & -60.6888 \\ 0.8704 & 38.0519 & -62.2513 \\ 0.9035 & 28.8742 & -59.0463 \\ \end{matrix} \right]\,\! }[/math]
- [math]\displaystyle{ {{\nu }^{(0)}}=\left[ \begin{matrix} g_{1}^{(0)} \\ g_{2}^{(0)} \\ g_{3}^{(0)} \\ \end{matrix} \right]=\left[ \begin{matrix} 94.16 \\ 0.615 \\ 0.731 \\ \end{matrix} \right]\,\! }[/math]
The estimate of the parameters [math]\displaystyle{ {{\nu }^{(0)}}\,\! }[/math] is given by:
- [math]\displaystyle{ \begin{align} \hat{v}&=\left ( D^{(0)}D^{(0)} \right )^{-1}D^{(0)}Y^{(0)} \\ &=\begin{bmatrix}0.061575\\ 0.000222\\ 0.001123\end{bmatrix} \end{align} }[/math]
The revised estimated regression coefficients in matrix form are:
- [math]\displaystyle{ \begin{align} g^{(1)}&=g^{(0)} + \hat{v}^{(0)} \\ &= \begin{bmatrix}94.16\\ 0.615\\ 0.731\end{bmatrix}+\begin{bmatrix}0.061575\\ 0.000222\\ 0.001123\end{bmatrix} \\ &=\begin{bmatrix}94.2216\\ 0.6152\\ 0.7321\end{bmatrix} \end{align} }[/math]
If the Gauss-Newton method works effectively, then the relationship [math]\displaystyle{ {{Q}^{(k+1)}}\lt {{Q}^{(k)}}\,\! }[/math] has to hold, meaning that [math]\displaystyle{ {{g}^{(k+1)}}\,\! }[/math] gives better estimates than [math]\displaystyle{ {{g}^{(k)}}\,\! }[/math], after [math]\displaystyle{ k\,\! }[/math]. With the starting coefficients, [math]\displaystyle{ {{g}^{(0)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} Q^{0}&=\sum_{i=1}^{N}\left [ Y_{i}-f\left ( T_{i}, g^{(0)} \right ) \right ]^{2}\\ &= 0.045622 \end{align} }[/math]
And with the coefficients at the end of the first iteration, [math]\displaystyle{ {{g}^{(1)}}\,\! }[/math], [math]\displaystyle{ Q\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} Q^{1}&=\sum_{i=1}^{N}\left [ Y_{i}-f\left ( T_{i}, g^{(1)} \right ) \right ]^{2}\\ &= 0.041439 \end{align} }[/math]
Therefore, it can be justified that the Gauss-Newton method works in the right direction. The iterations are continued until the relationship [math]\displaystyle{ Q^{(s-1)}-Q^{(s)}\simeq 0 }[/math] is satisfied. Note that the RGA software uses a different analysis method called the Levenberg-Marquardt. This method utilizes the best features of the Gauss-Newton method and the method of the steepest descent, and occupies a middle ground between these two methods. The estimated parameters using RGA are shown in the figure below.
They are:
- [math]\displaystyle{ \begin{align} & \widehat{a}= & 0.9422 \\ & \widehat{b}= & 0.6152 \\ & \widehat{c}= & 0.7321 \end{align}\,\! }[/math]
The Gompertz reliability growth curve is:
- [math]\displaystyle{ R=0.9422{{(0.6152)}^{{{0.7321}^{T}}}}\,\! }[/math]
- The achievable reliability at the end of the 12-month period of design and development is:
- [math]\displaystyle{ \begin{align} R&=0.9422(0.6152)^{0.7321} &=0.9314 \end{align}\,\! }[/math]
- The maximum achievable reliability from Step 2, or from the value of [math]\displaystyle{ a\,\! }[/math], is 0.9422.
- The predicted reliability values, as calculated from the standard Gompertz model, are compared with the actual data in the table below. It may be seen in the table that the Gompertz curve appears to provide a very good fit for the data used because the equation reproduces the available data with less than 1% error. The standard Gompertz model is plotted in the figure below the table. The plot identifies the type of reliability growth curve that the equation represents.
Comparison of the Predicted Reliabilities with the Actual Data Growth Time [math]\displaystyle{ T\,\! }[/math](months) Gompertz Reliability(%) Raw Data Reliability(%) 0 57.97 58.00 1 66.02 66.00 2 72.62 72.50 3 77.87 78.00 4 81.95 82.00 5 85.07 85.00 6 87.43 7 89.20 8 90.52 9 91.50 10 92.22 11 92.75 12 93.14