Power Law Model Confidence Bounds Example: Difference between revisions
Kate Racaza (talk | contribs) (Created page with '<noinclude>{{Banner RGA Examples}}{{Navigation box}} ''These examples appear in the [[Repairable_Systems_Analysis|Reliability Growth and Repairable System Analysis Reference book…') |
Lisa Hacker (talk | contribs) No edit summary |
||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner RGA Examples}}{{Navigation box}} | <noinclude>{{Banner RGA Examples}}{{Navigation box}} | ||
''These examples appear in the [ | ''These examples appear in the [https://help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis Reliability growth reference]''. | ||
</noinclude> | </noinclude> | ||
Using the data from the <noinclude>[[Power Law Model Parameter Estimation Example]]</noinclude><includeonly>power law model example given above</includeonly>, calculate the mission reliability at <math>t=2000\,\!</math> hours and mission time <math>d=40\,\!</math> hours along with the confidence bounds at the 90% confidence level. | Using the data from the <noinclude>[[Power Law Model Parameter Estimation Example]]</noinclude><includeonly>power law model example given above</includeonly>, calculate the mission reliability at <math>t=2000\,\!</math> hours and mission time <math>d=40\,\!</math> hours along with the confidence bounds at the 90% confidence level. | ||
'''Solution''' | '''Solution''' | ||
| Line 10: | Line 9: | ||
The maximum likelihood estimates of <math>\widehat{\lambda }\,\!</math> and <math>\widehat{\beta }\,\!</math> from the example are: | The maximum likelihood estimates of <math>\widehat{\lambda }\,\!</math> and <math>\widehat{\beta }\,\!</math> from the example are: | ||
:<math>\begin{align} | |||
\widehat{\beta }= & 0.45300 \\ | \widehat{\beta }= & 0.45300 \\ | ||
\widehat{\lambda }= & 0.36224 | \widehat{\lambda }= & 0.36224 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
The mission reliability at <math>t=2000\,\!</math> for mission time <math>d=40\,\!</math> is: | The mission reliability at <math>t=2000\,\!</math> for mission time <math>d=40\,\!</math> is: | ||
:<math>\begin{align} | |||
\widehat{R}(t)= & {{e}^{-\left[ \lambda {{\left( t+d \right)}^{\beta }}-\lambda {{t}^{\beta }} \right]}} \\ | \widehat{R}(t)= & {{e}^{-\left[ \lambda {{\left( t+d \right)}^{\beta }}-\lambda {{t}^{\beta }} \right]}} \\ | ||
= & 0.90292 | = & 0.90292 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
At the 90% confidence level and <math>T=2000\,\!</math> hours, the Fisher matrix confidence bounds for the mission reliability for mission time <math>d=40\,\!</math> are given by: | |||
:<math>CB=\frac{\widehat{R}(t)}{\widehat{R}(t)+(1-\widehat{R}(t)){{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\widehat{R}(t))}/\left[ \widehat{R}(t)(1-\widehat{R}(t)) \right]}}}\,\!</math> | |||
:<math>\begin{align} | |||
{{[\widehat{R}(t)]}_{L}}= & 0.83711 \\ | {{[\widehat{R}(t)]}_{L}}= & 0.83711 \\ | ||
{{[\widehat{R}(t)]}_{U}}= & 0.94392 | {{[\widehat{R}(t)]}_{U}}= & 0.94392 | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
The Crow confidence bounds for the mission reliability are: | The Crow confidence bounds for the mission reliability are: | ||
:<math>\begin{align} | |||
{{[\widehat{R}(t)]}_{L}}= & {{[\widehat{R}(\tau )]}^{\tfrac{1}{{{\Pi }_{1}}}}} \\ | {{[\widehat{R}(t)]}_{L}}= & {{[\widehat{R}(\tau )]}^{\tfrac{1}{{{\Pi }_{1}}}}} \\ | ||
= & {{[0.90292]}^{\tfrac{1}{0.71440}}} \\ | = & {{[0.90292]}^{\tfrac{1}{0.71440}}} \\ | ||
| Line 46: | Line 41: | ||
\end{align}\,\!</math> | \end{align}\,\!</math> | ||
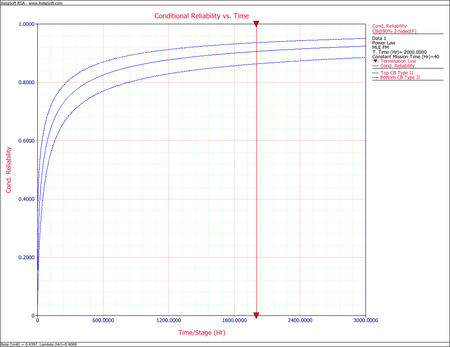
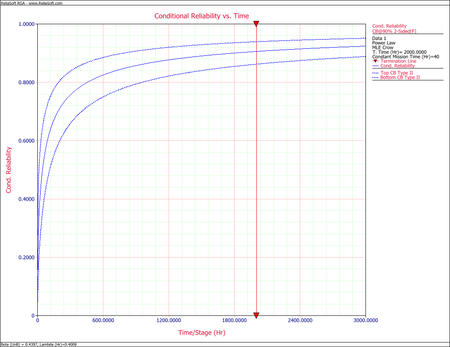
The next two figures show the Fisher matrix and Crow confidence bounds on mission reliability for mission time <math>d=40\,\!</math>. | |||
The next two figures show the Fisher | |||
[[Image:rga13.3.png|center|450px | [[Image:rga13.3.png|center|450px]] | ||
[[Image:rga13.4.png|center|450px | [[Image:rga13.4.png|center|450px]] | ||
Latest revision as of 21:23, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
These examples appear in the Reliability growth reference.
Using the data from the Power Law Model Parameter Estimation Example, calculate the mission reliability at [math]\displaystyle{ t=2000\,\! }[/math] hours and mission time [math]\displaystyle{ d=40\,\! }[/math] hours along with the confidence bounds at the 90% confidence level.
Solution
The maximum likelihood estimates of [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] and [math]\displaystyle{ \widehat{\beta }\,\! }[/math] from the example are:
- [math]\displaystyle{ \begin{align} \widehat{\beta }= & 0.45300 \\ \widehat{\lambda }= & 0.36224 \end{align}\,\! }[/math]
The mission reliability at [math]\displaystyle{ t=2000\,\! }[/math] for mission time [math]\displaystyle{ d=40\,\! }[/math] is:
- [math]\displaystyle{ \begin{align} \widehat{R}(t)= & {{e}^{-\left[ \lambda {{\left( t+d \right)}^{\beta }}-\lambda {{t}^{\beta }} \right]}} \\ = & 0.90292 \end{align}\,\! }[/math]
At the 90% confidence level and [math]\displaystyle{ T=2000\,\! }[/math] hours, the Fisher matrix confidence bounds for the mission reliability for mission time [math]\displaystyle{ d=40\,\! }[/math] are given by:
- [math]\displaystyle{ CB=\frac{\widehat{R}(t)}{\widehat{R}(t)+(1-\widehat{R}(t)){{e}^{\pm {{z}_{\alpha }}\sqrt{Var(\widehat{R}(t))}/\left[ \widehat{R}(t)(1-\widehat{R}(t)) \right]}}}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{[\widehat{R}(t)]}_{L}}= & 0.83711 \\ {{[\widehat{R}(t)]}_{U}}= & 0.94392 \end{align}\,\! }[/math]
The Crow confidence bounds for the mission reliability are:
- [math]\displaystyle{ \begin{align} {{[\widehat{R}(t)]}_{L}}= & {{[\widehat{R}(\tau )]}^{\tfrac{1}{{{\Pi }_{1}}}}} \\ = & {{[0.90292]}^{\tfrac{1}{0.71440}}} \\ = & 0.86680 \\ {{[\widehat{R}(t)]}_{U}}= & {{[\widehat{R}(\tau )]}^{\tfrac{1}{{{\Pi }_{2}}}}} \\ = & {{[0.90292]}^{\tfrac{1}{1.6051}}} \\ = & 0.93836 \end{align}\,\! }[/math]
The next two figures show the Fisher matrix and Crow confidence bounds on mission reliability for mission time [math]\displaystyle{ d=40\,\! }[/math].