Crow-AMSAA Parameter Estimation Example: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(4 intermediate revisions by 3 users not shown)
Line 1: Line 1:
<noinclude>{{Banner RGA Examples}}
<noinclude>{{Banner RGA Examples}}
''This example appears in the [[Crow-AMSAA (NHPP)|Reliability Growth and Repairable System Analysis Reference book]]''.
''This example appears in the [https://help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis Reliability growth reference]''.
</noinclude>
</noinclude>


A prototype of a system was tested with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
A prototype of a system was tested with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.


<center>'''Developmental test data''' </center>
<center>'''Developmental Test Data''' </center>
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5"
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5"
!Row
!Row
Line 89: Line 89:
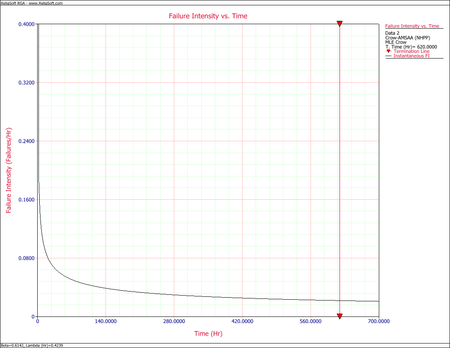
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is <math>\tfrac{1}{0.0217906}\,\!</math> or 46 hours.
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is <math>\tfrac{1}{0.0217906}\,\!</math> or 46 hours.


[[Image:FIvsTimeExample1.png|center|500px|Failure Intensity vs. Time plot]]
[[Image:FIvsTimeExample1.png|center|450px]]
 
 
====Confidence Bounds on Cumulative and Instantaneous Failure Intensity====
Using the values of <math>\hat{\beta }\,\!</math> and <math>\hat{\lambda }\,\!</math> estimated in the example given above, calculate the 90% 2-sided confidence bounds on the cumulative and instantaneous failure intensity. 
 
'''Solution'''
 
'''Fisher Matrix Bounds'''
 
The partial derivatives for the Fisher Matrix confidence bounds are:
 
:<math>\begin{align}
  \frac{{{\partial }^{2}}\Lambda }{\partial {{\lambda }^{2}}} = & -\frac{22}{{{0.4239}^{2}}}=-122.43 \\
  \frac{{{\partial }^{2}}\Lambda }{\partial {{\beta }^{2}}} = & -\frac{22}{{{0.6142}^{2}}}-0.4239\cdot {{620}^{0.6142}}{{(\ln 620)}^{2}}=-967.68 \\
  \frac{{{\partial }^{2}}\Lambda }{\partial \lambda \partial \beta }  = & -{{620}^{0.6142}}\ln 620=-333.64 
\end{align}\,\!</math>
 
The Fisher Matrix then becomes:
 
:<math>\begin{align}
\begin{bmatrix}122.43 & 333.64\\ 333.64 & 967.68\end{bmatrix}^{-1} & = \begin{bmatrix}Var(\hat{\lambda}) & Cov(\hat{\beta},\hat{\lambda})\\
Cov(\hat{\beta},\hat{\lambda}) & Var(\hat{\beta})\end{bmatrix} \\
& = \begin{bmatrix} 0.13519969 & -0.046614609\\ -0.046614609 & 0.017105343 \end{bmatrix}
\end{align}\,\!</math>
 
For <math>T=620\,\!</math> hours, the partial derivatives of the cumulative and instantaneous failure intensities are:
 
:<math>\begin{align}
  \frac{\partial {{\lambda }_{c}}(T)}{\partial \beta }=  & \hat{\lambda }{{T}^{\hat{\beta }-1}}\ln (T) \\
  =  & 0.4239\cdot {{620}^{-0.3858}}\ln 620 \\
  =  & 0.22811336 \\
  \frac{\partial {{\lambda }_{c}}(T)}{\partial \lambda }=  & {{T}^{\hat{\beta }-1}} \\
  =  & {{620}^{-0.3858}} \\
  =  & 0.083694185 
\end{align}\,\!</math>
 
:<math>\begin{align}
  \frac{\partial {{\lambda }_{i}}(T)}{\partial \beta }=  & \hat{\lambda }{{T}^{\hat{\beta }-1}}+\hat{\lambda }\hat{\beta }{{T}^{\hat{\beta }-1}}\ln T \\
  =  & 0.4239\cdot {{620}^{-0.3858}}+0.4239\cdot 0.6142\cdot {{620}^{-0.3858}}\ln 620 \\
  =  & 0.17558519 
\end{align}\,\!</math>
 
:<math>\begin{align}
  \frac{\partial {{\lambda }_{i}}(T)}{\partial \lambda }=  & \hat{\beta }{{T}^{\hat{\beta }-1}} \\
  =  & 0.6142\cdot {{620}^{-0.3858}} \\
  =  & 0.051404969 
\end{align}\,\!</math>
 
Therefore, the variances become:
 
:<math>\begin{align}
Var(\hat{\lambda_{c}}(T)) & = 0.22811336^{2}\cdot 0.017105343\ + 0.083694185^{2} \cdot 0.13519969\ -2\cdot 0.22811336\cdot 0.083694185\cdot 0.046614609 \\
& = 0.00005721408 \\
Var(\hat{\lambda_{i}}(T)) & = 0.17558519^{2}\cdot 0.01715343\ + 0.051404969^{2}\cdot 0.13519969\ -2\cdot 0.17558519\cdot 0.051404969\cdot 0.046614609 \\
&= 0.0000431393
\end{align}\,\!</math>
 
The cumulative and instantaneous failure intensities at <math>T=620\,\!</math> hours are:
 
:<math>\begin{align}
  {{\lambda }_{c}}(T)= & 0.03548 \\
{{\lambda }_{i}}(T)= & 0.02179 
\end{align}\,\!</math>
 
So, at the 90% confidence level and for <math>T=620\,\!</math> hours, the Fisher Matrix confidence bounds for the cumulative failure intensity are:
 
:<math>\begin{align}
  {{[{{\lambda }_{c}}(T)]}_{L}}= & 0.02499 \\
  {{[{{\lambda }_{c}}(T)]}_{U}}= & 0.05039 
\end{align}\,\!</math>
 
The confidence bounds for the instantaneous failure intensity are:
 
:<math>\begin{align}
  {{[{{\lambda }_{i}}(T)]}_{L}}= & 0.01327 \\
  {{[{{\lambda }_{i}}(T)]}_{U}}= & 0.03579 
\end{align}\,\!</math>
 
The following figures display plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous failure intensity, respectively.
 
[[Image:rga5.2.png|center|500px|Cumulative failure intensity with 2-sided 90% Fisher Matrix confidence bounds.]]
 
[[Image:rga5.3.png|center|500px|Instantaneous failure intensity with 2-sided 90% Fisher Matrix confidence bounds.]]
 
'''Crow Bounds'''
 
Given that the data is failure terminated, the Crow confidence bounds for the cumulative failure intensity at the 90% confidence level and for <math>T=620\,\!</math> hours are:
 
:<math>\begin{align}
  {{[{{\lambda }_{c}}(T)]}_{L}} = & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot t} \\
    = & \frac{29.787476}{2*620} \\
    = & 0.02402 \\
  {{[{{\lambda }_{c}}(T)]}_{U}} = & \frac{\chi _{1-\tfrac{\alpha }{2},2N}^{2}}{2\cdot t} \\
    = & \frac{60.48089}{2*620} \\
    = & 0.048775 
\end{align}\,\!</math>
 
The Crow confidence bounds for the instantaneous failure intensity at the 90% confidence level and for <math>T=620\,\!</math> hours are calculated by first estimating the bounds on the instantaneous MTBF. Once these are calculated, take the inverse as shown below. Details on the confidence bounds for instantaneous MTBF are presented [[Crow-AMSAA Confidence Bounds#Crow_Bounds_4|here]].
 
:<math>\begin{align}
  {{[{{\lambda }_{i}}(t)]}_{L}} = & \frac{1}{{{[MTB{{F}_{i}}]}_{U}}} \\
= & \frac{1}{MTB{{F}_{i}}\cdot U} \\
= & 0.01179 
\end{align}\,\!</math>
 
:<math>\begin{align}
  {{[{{\lambda }_{i}}(t)]}_{U}}=  & \frac{1}{{{[MTB{{F}_{i}}]}_{L}}} \\
  =  & \frac{1}{MTB{{F}_{i}}\cdot L} \\
  =  & 0.03253 
\end{align}\,\!</math>
 
The following figures display plots of the Crow confidence bounds for the cumulative and instantaneous failure intensity, respectively.
 
[[Image:rga5.4.png|center|500px|Cumulative failure intensity with 2-sided 90% Crow confidence bounds.]]
 
[[Image:rga5.5.png|center|500px|Instantaneous failure intensity with 2-sided 90% Crow confidence bounds.]]
 
 
====Confidence Bounds on Cumulative and Instantaneous MTBF====
Calculate the confidence bounds on the cumulative and instantaneous MTBF for the data from the example given above. 
 
'''Solution'''
 
'''Fisher Matrix Bounds'''
 
From the previous example:
 
:<math>\begin{align}
  Var(\hat{\lambda })  = & 0.13519969 \\
  Var(\hat{\beta })  = & 0.017105343 \\
  Cov(\hat{\beta },\hat{\lambda })  = & -0.046614609 
\end{align}\,\!</math>
 
And for <math>T=620\,\!</math> hours, the partial derivatives of the cumulative and instantaneous MTBF are:
 
:<math>\begin{align}
  \frac{\partial {{m}_{c}}(T)}{\partial \beta }= & -\frac{1}{\hat{\lambda }}{{T}^{1-\hat{\beta }}}\ln T \\
  = & -\frac{1}{0.4239}{{620}^{0.3858}}\ln 620 \\
  = & -181.23135 \\
  \frac{\partial {{m}_{c}}(T)}{\partial \lambda } = & -\frac{1}{{{\hat{\lambda }}^{2}}}{{T}^{1-\hat{\beta }}} \\
  = & -\frac{1}{{{0.4239}^{2}}}{{620}^{0.3858}} \\
  = & -66.493299 \\
  \frac{\partial {{m}_{i}}(T)}{\partial \beta } = & -\frac{1}{\hat{\lambda }{{\hat{\beta }}^{2}}}{{T}^{1-\beta }}-\frac{1}{\hat{\lambda }\hat{\beta }}{{T}^{1-\hat{\beta }}}\ln T \\
= & -\frac{1}{0.4239\cdot {{0.6142}^{2}}}{{620}^{0.3858}}-\frac{1}{0.4239\cdot 0.6142}{{620}^{0.3858}}\ln 620 \\
= & -369.78634 \\
  \frac{\partial {{m}_{i}}(T)}{\partial \lambda } = & -\frac{1}{{{\hat{\lambda }}^{2}}\hat{\beta }}{{T}^{1-\hat{\beta }}} \\
= & -\frac{1}{{{0.4239}^{2}}\cdot 0.6142}\cdot {{620}^{0.3858}} \\
= & -108.26001 
\end{align}\,\!</math>
 
Therefore, the variances become:
 
:<math>\begin{align}
  Var({{\hat{m}}_{c}}(T)) = & {{\left( -181.23135 \right)}^{2}}\cdot 0.017105343+{{\left( -66.493299 \right)}^{2}}\cdot 0.13519969 \\
  & -2\cdot \left( -181.23135 \right)\cdot \left( -66.493299 \right)\cdot 0.046614609 \\
  = & 36.113376 
\end{align}\,\!</math>
 
:<math>\begin{align}
  Var({{\hat{m}}_{i}}(T))  = & {{\left( -369.78634 \right)}^{2}}\cdot 0.017105343+{{\left( -108.26001 \right)}^{2}}\cdot 0.13519969 \\
  & -2\cdot \left( -369.78634 \right)\cdot \left( -108.26001 \right)\cdot 0.046614609 \\
= & 191.33709 
\end{align}\,\!</math>
 
So, at 90% confidence level and <math>T=620\,\!</math> hours, the Fisher Matrix confidence bounds are:
 
:<math>\begin{align}
  {{[{{m}_{c}}(T)]}_{L}}  = & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\
  = & 19.84581 \\
  {{[{{m}_{c}}(T)]}_{U}} = & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\
  = & 40.01927 
\end{align}\,\!</math>
 
:<math>\begin{align}
  {{[{{m}_{i}}(T)]}_{L}}  = & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\
  = & 27.94261 \\
{{[{{m}_{i}}(T)]}_{U}} = & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha }}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\
  = & 75.34193 
\end{align}\,\!</math>
 
The following two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBFs.
 
[[Image:rga5.6.png|center|500px|Cumulative MTBF with 2-sided 90% Fisher Matrix confidence bounds.]]
 
[[Image:rga5.7.png|center|500px|Instantaneous MTBF with 2-sided Fisher Matrix confidence bounds.]]
 
'''Crow Bounds'''
 
The Crow confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% confidence level and for <math>T=620\,\!</math> hours are:
 
:<math>\begin{align}
  {{[{{m}_{c}}(T)]}_{L}}  = & \frac{1}{{{[{{\lambda }_{c}}(T)]}_{U}}} \\
  = & 20.5023 \\
  {{[{{m}_{c}}(T)]}_{U}}  = & \frac{1}{{{[{{\lambda }_{c}}(T)]}_{L}}} \\
  = & 41.6282 
\end{align}\,\!</math>
 
:<math>\begin{align}
  {{[MTB{{F}_{i}}]}_{L}} = & MTB{{F}_{i}}\cdot {{\Pi }_{1}} \\
  = & 30.7445 \\
  {{[MTB{{F}_{i}}]}_{U}}  = & MTB{{F}_{i}}\cdot {{\Pi }_{2}} \\
  = & 84.7972 
\end{align}\,\!</math>
 
The figures below show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
 
[[Image:rga5.8.png|center|500px|Cumulative MTBF with 2-sided 90% Crow confidence bounds.]]
 
[[Image:rga5.9.png|center|500px|Instantaneous MTBF with 2-sided 90% Crow confidence bounds.]]
Confidence bounds can also be obtained on the parameters <math>\hat{\beta }\,\!</math> and <math>\hat{\lambda }\,\!</math>. For Fisher Matrix confidence bounds:
 
:<math>\begin{align}
  {{\beta }_{L}}  = & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\
  = & 0.4325 \\
{{\beta }_{U}}  = & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\
  = & 0.8722 
\end{align}\,\!</math>
 
and:
 
:<math>\begin{align}
  {{\lambda }_{L}}  = & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\
  = & 0.1016 \\
  {{\lambda }_{U}}  = & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\
  = & 1.7691 
\end{align}\,\!</math>
 
For Crow confidence bounds:
 
:<math>\begin{align}
  {{\beta }_{L}}= & 0.4527 \\
  {{\beta }_{U}}= & 0.9350 
\end{align}\,\!</math>
 
and:
 
:<math>\begin{align}
  {{\lambda }_{L}}= & 0.2870 \\
  {{\lambda }_{U}}= & 0.5827 
\end{align}\,\!</math>

Latest revision as of 21:21, 18 September 2023

RGA Examples Banner.png


New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.



This example appears in the Reliability growth reference.


A prototype of a system was tested with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.

Developmental Test Data
Row Time to Event (hr) [math]\displaystyle{ ln{(T)}\,\! }[/math]
1 2.7 0.99325
2 10.3 2.33214
3 12.5 2.52573
4 30.6 3.42100
5 57.0 4.04305
6 61.3 4.11578
7 80.0 4.38203
8 109.5 4.69592
9 125.0 4.82831
10 128.6 4.85671
11 143.8 4.96842
12 167.9 5.12337
13 229.2 5.43459
14 296.7 5.69272
15 320.6 5.77019
16 328.2 5.79362
17 366.2 5.90318
18 396.7 5.98318
19 421.1 6.04287
20 438.2 6.08268
21 501.2 6.21701
22 620.0 6.42972

Solution

For the failure terminated test, [math]\displaystyle{ {\beta}\,\! }[/math] is:

[math]\displaystyle{ \begin{align} \widehat{\beta }&=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} \\ &=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} \\ \end{align}\,\! }[/math]

where:

[math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355\,\! }[/math]

Then:

[math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142\,\! }[/math]

And for [math]\displaystyle{ {\lambda}\,\! }[/math] :

[math]\displaystyle{ \begin{align} \widehat{\lambda }&=\frac{n}{{{T}^{*\beta }}} \\ & =\frac{22}{{{620}^{0.6142}}}=0.4239 \\ \end{align}\,\! }[/math]

Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T)\,\! }[/math] becomes:

[math]\displaystyle{ \begin{align} {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align}\,\! }[/math]

The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906}\,\! }[/math] or 46 hours.

FIvsTimeExample1.png
Retrieved from "https://www.reliawiki.com/index.php?title=Crow-AMSAA_Parameter_Estimation_Example&oldid=66123"