Power Law Model Parameter Estimation Example

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

These examples appear in the Reliability growth reference.

For the data in the following table, the starting time for each system is equal to 0 and the ending time for each system is 2,000 hours. Calculate the maximum likelihood estimates [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] and [math]\displaystyle{ \widehat{\beta }\,\! }[/math].

Repairable System Failure Data
System 1 ( [math]\displaystyle{ {{X}_{i1}}\,\! }[/math] )	System 2 ( [math]\displaystyle{ {{X}_{i2}}\,\! }[/math] )	System 3 ( [math]\displaystyle{ {{X}_{i3}}\,\! }[/math] )
1.2	1.4	0.3
55.6	35.0	32.6
72.7	46.8	33.4
111.9	65.9	241.7
121.9	181.1	396.2
303.6	712.6	444.4
326.9	1005.7	480.8
1568.4	1029.9	588.9
1913.5	1675.7	1043.9
	1787.5	1136.1
	1867.0	1288.1
		1408.1
		1439.4
		1604.8
[math]\displaystyle{ {{N}_{1}}=9\,\! }[/math]	[math]\displaystyle{ {{N}_{2}}=11\,\! }[/math]	[math]\displaystyle{ {{N}_{3}}=14\,\! }[/math]

Solution

Because the starting time for each system is equal to zero and each system has an equivalent ending time, the general equations for [math]\displaystyle{ \widehat{\beta }\,\! }[/math] and [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] reduce to the closed form equations. The maximum likelihood estimates of [math]\displaystyle{ \hat{\beta }\,\! }[/math] and [math]\displaystyle{ \hat{\lambda }\,\! }[/math] are then calculated as follows:

[math]\displaystyle{ \widehat{\beta }= \frac{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}}}{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,\underset{i=1}{\overset{{{N}_{q}}}{\mathop{\sum }}}\,\ln (\tfrac{T}{{{X}_{iq}}})} = 0.45300 }[/math]

[math]\displaystyle{ \widehat{\lambda }= \frac{\underset{q=1}{\overset{K}{\mathop{\sum }}}\,{{N}_{q}}}{K{{T}^{\beta }}} = 0.36224 \,\! }[/math]

The system failure intensity function is then estimated by:

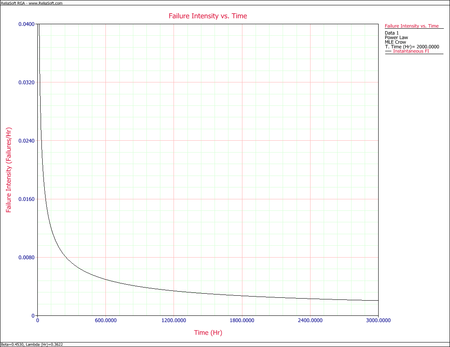
[math]\displaystyle{ \widehat{u}(t)=\widehat{\lambda }\widehat{\beta }{{t}^{\widehat{\beta }-1}},\text{ }t\gt 0\,\! }[/math]

The next figure is a plot of [math]\displaystyle{ \widehat{u}(t)\,\! }[/math] over the period (0, 3000). Clearly, the estimated failure intensity function is most representative over the range of the data and any extrapolation should be viewed with the usual caution.