Example Calculating System Reliability with Duty Cycles: Difference between revisions
No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner BlockSim Examples}} | <noinclude>{{Banner BlockSim Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/system_analysis System analysis reference]''. | ||
</noinclude> | </noinclude> | ||
| Line 53: | Line 53: | ||
[[Image:Fig 5.15.PNG|center|450px|<div align="center"> Result for the computer system reliability.</div>]] | [[Image:Fig 5.15.PNG|center|450px|<div align="center"> Result for the computer system reliability.</div>|link=]] | ||
Latest revision as of 20:57, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.
This example appears in the System analysis reference.
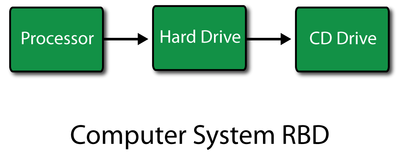
Consider a computer system with three components: a processor, a hard drive and a CD drive in series as shown next. Assume that all three components follow a Weibull failure distribution. The processor has the following parameters, [math]\displaystyle{ {{\beta }_{1}}=1.5\,\! }[/math] and [math]\displaystyle{ {{\eta }_{1}}=5000\,\! }[/math]. For the hard drive, the parameters are [math]\displaystyle{ {{\beta }_{2}}=2.5\,\! }[/math] and [math]\displaystyle{ {{\eta }_{2}}=3000\,\! }[/math], and for the CD drive they are [math]\displaystyle{ {{\beta }_{3}}=2\,\! }[/math] and [math]\displaystyle{ {{\eta }_{3}}=4000\,\! }[/math]. Determine the reliability of the computer system after one year (365 days) of operation, assuming that the CD drive is used only 30% of the time.
Solution
The reliability of the processor after 365 days of operation is given by:
- [math]\displaystyle{ \begin{align} {{R}_{processor}}(365)= & {{e}^{-{{\left( \tfrac{365}{{{\eta }_{1}}} \right)}^{{{\beta }_{1}}}}}} \\ = & {{e}^{-{{\left( \tfrac{365}{5000} \right)}^{1.5}}}} \\ = & 0.9805\text{ or }98.05% \end{align}\,\! }[/math]
The reliability of the hard drive after 365 days of operation is given by:
- [math]\displaystyle{ \begin{align} {{R}_{harddrive}}(365)= & {{e}^{-{{\left( \tfrac{365}{{{\eta }_{2}}} \right)}^{{{\beta }_{2}}}}}} \\ = & {{e}^{-{{\left( \tfrac{365}{3000} \right)}^{2.5}}}} \\ = & 0.9948\text{ or }99.48% \end{align}\,\! }[/math]
The reliability of the CD drive after 365 days of operation (taking into account the 30% operation using a duty cycle of 0.3) is given by:
- [math]\displaystyle{ \begin{align} {{R}_{CDdrive}}(365)= & {{e}^{-{{\left( \tfrac{{{d}_{c}}\times 365}{{{\eta }_{3}}} \right)}^{{{\beta }_{3}}}}}} \\ = & {{e}^{-{{\left( \tfrac{0.3\times 365}{4000} \right)}^{2}}}} \\ = & 0.9993\text{ or }99.93% \end{align}\,\! }[/math]
Thus the reliability of the computer system after 365 days of operation is:
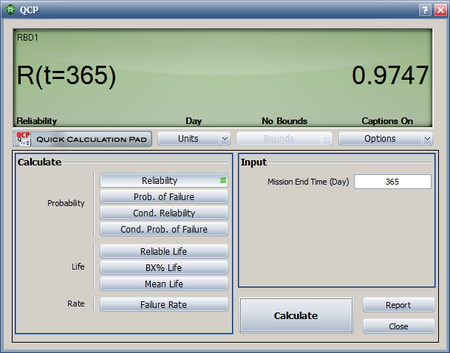
- [math]\displaystyle{ \begin{align} {{R}_{s}}(365)= & {{R}_{processor}}(365)\cdot {{R}_{harddrive}}(365)\cdot {{R}_{CDdrive}}(365) \\ = & 0.9805\cdot 0.9948\cdot 0.9993 \\ = & 0.9747\text{ or }97.47% \end{align}\,\! }[/math]
The result can also be obtained in BlockSim by creating an RBD of the system and using the Quick Calculation Pad (QCP) to calculate the reliability, as shown in the following figure.