Mixed Data - Crow Extended Example: Difference between revisions
mNo edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner RGA Examples}} | <noinclude>{{Banner RGA Examples}} | ||
''This example appears in the [ | ''This example appears in the [https://help.reliasoft.com/reference/reliability_growth_and_repairable_system_analysis Reliability growth reference]''. | ||
</noinclude> | </noinclude> | ||
| Line 46: | Line 46: | ||
The table also gives the classifications of the failure modes. There are 5 BD modes. The average effectiveness factor for the BD modes is 0.7. Do the following: | The table also gives the classifications of the failure modes. There are 5 BD modes. The average effectiveness factor for the BD modes is 0.7. Do the following: | ||
#Calculate the demonstrated reliability at the end of the test. | |||
#Calculate the growth potential reliability. | |||
'''Solution''' | '''Solution''' | ||
<ol><li> | |||
Based on the equations presented in [[Crow-AMSAA (NHPP)|Crow-AMSAA (NHPP)]], the parameters of the Crow-AMSAA (NHPP) model are estimated as follows: | Based on the equations presented in [[Crow-AMSAA (NHPP)|Crow-AMSAA (NHPP)]], the parameters of the Crow-AMSAA (NHPP) model are estimated as follows: | ||
| Line 94: | Line 93: | ||
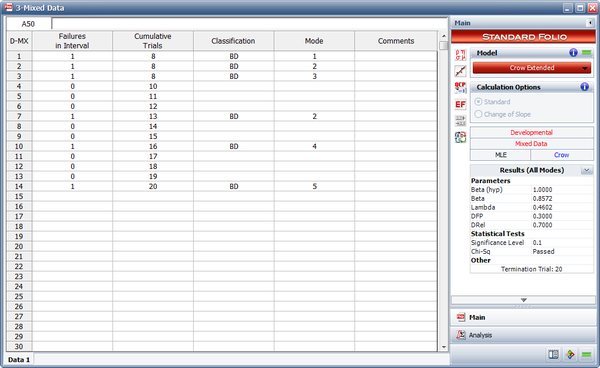
The next figure shows the data sheet as calculated in the RGA software. | The next figure shows the data sheet as calculated in the RGA software. | ||
[[Image:rga9.12.png|center| | [[Image:rga9.12.png|center|600px]] | ||
</li> | |||
The growth potential unreliability is: | <li>The growth potential unreliability is: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 115: | Line 114: | ||
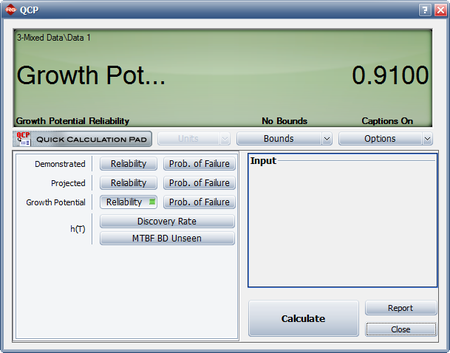
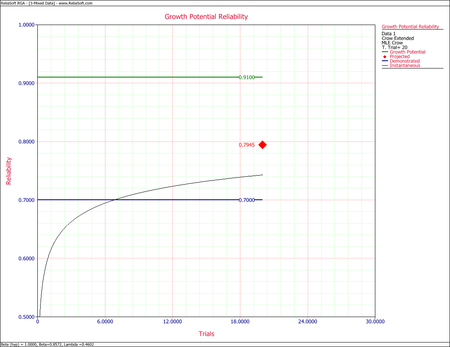
The figures below show the calculation of the growth potential reliability for the mixed data using the RGA software's QCP, followed by the growth potential plot. | The figures below show the calculation of the growth potential reliability for the mixed data using the RGA software's QCP, followed by the growth potential plot. | ||
[[Image:rga9.13.png|center| | [[Image:rga9.13.png|center|450px]] | ||
[[Image:rga9.14.png|center| | [[Image:rga9.14.png|center|450px]]</li> | ||
</ol> | |||
Latest revision as of 20:53, 18 September 2023
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability growth reference.
A one-shot system underwent reliability growth testing for a total of 20 trials. The test was performed as a combination of groups of units with the same configuration and individual trials. The following table shows the data set. The Failures in Interval column specifies the number of failures that occurred in each interval and the Cumulative Trials column specifies the cumulative number of trials at the end of that interval. In other words, the first three rows contain the data from the first trial, in which 8 units with the same configuration were tested and 3 failures (with different failure modes) were observed. The next row contains data from the second trial, in which 2 units with the same configuration were tested and no failures occurred. And so on.
| Mixed Data | |||
| Failures in Interval | Cumulative Trials | Classification | Mode |
|---|---|---|---|
| 1 | 8 | BD | 1 |
| 1 | 8 | BD | 2 |
| 1 | 8 | BD | 3 |
| 0 | 10 | ||
| 0 | 11 | ||
| 0 | 12 | ||
| 1 | 13 | BD | 2 |
| 0 | 14 | ||
| 0 | 15 | ||
| 1 | 16 | BD | 4 |
| 0 | 17 | ||
| 0 | 18 | ||
| 0 | 19 | ||
| 1 | 20 | BD | 5 |
The table also gives the classifications of the failure modes. There are 5 BD modes. The average effectiveness factor for the BD modes is 0.7. Do the following:
- Calculate the demonstrated reliability at the end of the test.
- Calculate the growth potential reliability.
Solution
-
Based on the equations presented in Crow-AMSAA (NHPP), the parameters of the Crow-AMSAA (NHPP) model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.8572\,\! }[/math]
- [math]\displaystyle{ \widehat{\lambda }=0.4602\,\! }[/math]
- [math]\displaystyle{ \hat{\lambda }=\frac{n}{T_{n}^{\hat{\beta }}}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \hat{\lambda }= & \frac{n}{{{T}_{n}}} \\ = & \frac{6}{20} \\ = & 0.3 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 \end{align}\,\! }[/math]
- [math]\displaystyle{ {{Q}_{i}}(20)=\widehat{\lambda }=0.3\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{R}_{i}}(20)= & 1-{{Q}_{i}}(20) \\ = & 1-0.3 \\ = & 0.7 \end{align}\,\! }[/math]
- The growth potential unreliability is:
- [math]\displaystyle{ \begin{align} {{\widehat{Q}}_{GP}}(T)= & \left( \frac{{{N}_{A}}}{T}+\underset{i=1}{\overset{M}{\mathop \sum }}\,(1-{{d}_{i}})\frac{{{N}_{i}}}{T} \right) \\ = & \underset{i=1}{\overset{M}{\mathop \sum }}\,(1-0.7)\frac{{{N}_{i}}}{T} \\ = & 0.3*(\frac{1+1+1+1+1+1)}{20} \\ = & 0.09 \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} {{\widehat{R}}_{GP}}(T) = & 1-{{\widehat{Q}}_{GP}}(T) \\ = & 1-0.09 \\ = & 0.91 \end{align}\,\! }[/math]