Appendix: Log-Likelihood Equations: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
|||
| (25 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Template: | {{Template:LDABOOK|Appendix D|Log-Likelihood Equations}} | ||
This appendix covers the log-likelihood functions and their associated partial derivatives for most of the distributions available in Weibull++. These distributions are discussed in more detail in the chapter for each distribution. | This appendix covers the log-likelihood functions and their associated partial derivatives for most of the distributions available in Weibull++. These distributions are discussed in more detail in the chapter for each distribution. | ||
| Line 9: | Line 9: | ||
\ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{{{T}_{i}}}{\eta } \right)}^{\beta }}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }} \\ | \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{{{T}_{i}}}{\eta } \right)}^{\beta }}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }} \\ | ||
& \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}} \right] | & \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}} \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
| Line 23: | Line 23: | ||
:*<math>FI\,\!</math> is the number of interval failure data groups | :*<math>FI\,\!</math> is the number of interval failure data groups | ||
:*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in <math>{{i}^{th}}\,\!</math> group of data intervals | :*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in <math>{{i}^{th}}\,\!</math> group of data intervals | ||
:*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the <math>{{i}^{th}}\,\!</math> | :*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the <math>{{i}^{th}}\,\!</math> interval | ||
:*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | :*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | ||
| Line 35: | Line 35: | ||
& -\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta }}\ln \left( \frac{{{T}_{i}}}{\eta } \right)-\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }}\ln \left( \frac{T_{i}^{\prime }}{\eta } \right) \\ | & -\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta }}\ln \left( \frac{{{T}_{i}}}{\eta } \right)-\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }}\ln \left( \frac{T_{i}^{\prime }}{\eta } \right) \\ | ||
& +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}+{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}} | & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}+{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 43: | Line 43: | ||
& +\frac{\beta }{\eta }\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }} \\ | & +\frac{\beta }{\eta }\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }} \\ | ||
& +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\left( \tfrac{\beta }{\eta } \right){{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-\left( \tfrac{\beta }{\eta } \right){{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}} | & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\left( \tfrac{\beta }{\eta } \right){{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-\left( \tfrac{\beta }{\eta } \right){{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
==== The Three-Parameter Weibull==== | ==== The Three-Parameter Weibull==== | ||
| Line 52: | Line 52: | ||
& \\ | & \\ | ||
& +\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}} \right] | & +\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}} \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
| Line 78: | Line 78: | ||
& +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \\ | & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \\ | ||
& +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} | & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 86: | Line 86: | ||
& +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{\eta }{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \\ | & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{\eta }{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \\ | ||
& -\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{\eta }{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} | & -\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{\eta }{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 95: | Line 95: | ||
& +\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }-\gamma }{\eta } \right)}^{\beta }}\left( \frac{\beta }{T_{i}^{\prime }-\gamma } \right) \\ | & +\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }-\gamma }{\eta } \right)}^{\beta }}\left( \frac{\beta }{T_{i}^{\prime }-\gamma } \right) \\ | ||
& +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{T_{Li}^{\prime \prime }-\gamma }{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-\tfrac{\beta }{T_{Ri}^{\prime \prime }-\gamma }{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} | & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{T_{Li}^{\prime \prime }-\gamma }{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-\tfrac{\beta }{T_{Ri}^{\prime \prime }-\gamma }{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
It should be pointed out that the solution to the three-parameter Weibull via MLE is not always stable and can collapse if <math>\beta \sim 1.\,\!</math> In estimating the true MLE of the three-parameter Weibull distribution, two difficulties arise. The first is a problem of non-regularity and the second is the parameter divergence problem [14]. | It should be pointed out that the solution to the three-parameter Weibull via MLE is not always stable and can collapse if <math>\beta \sim 1.\,\!</math> In estimating the true MLE of the three-parameter Weibull distribution, two difficulties arise. The first is a problem of non-regularity and the second is the parameter divergence problem, as discussed in Hirose [[Appendix:_Life_Data_Analysis_References|[14]]]. | ||
Non-regularity occurs when <math>\beta \le 2.\,\!</math> In general, there are no MLE solutions in the region of <math>0<\beta <1.\,\!</math> When <math>1<\beta <2,\,\!</math> MLE solutions exist but are not asymptotically normal [14]. In the case of non-regularity, the solution is treated anomalously. | Non-regularity occurs when <math>\beta \le 2.\,\!</math> In general, there are no MLE solutions in the region of <math>0<\beta <1.\,\!</math> When <math>1<\beta <2,\,\!</math> MLE solutions exist but are not asymptotically normal, as discussed in Hirose [[Appendix:_Life_Data_Analysis_References|[14]]]. In the case of non-regularity, the solution is treated anomalously. | ||
Weibull++ attempts to find a solution in all of the regions using a variety of methods, but the user should be forewarned that not all possible data can be addressed. Thus, some solutions using MLE for the three-parameter Weibull will fail when the algorithm has reached predefined limits or fails to converge. In these cases, the user can change to the non-true MLE approach (in Weibull++ Application Setup), where <math>\gamma \,\!</math> is estimated using non-linear regression. Once <math>\gamma \,\!</math> is obtained, the MLE estimates of <math>\widehat{\beta }\,\!</math> and <math>\widehat{\eta }\,\!</math> are computed using the transformation <math>T_{i}^{\prime }=({{T}_{i}}-\gamma ).\,\!</math> | Weibull++ attempts to find a solution in all of the regions using a variety of methods, but the user should be forewarned that not all possible data can be addressed. Thus, some solutions using MLE for the three-parameter Weibull will fail when the algorithm has reached predefined limits or fails to converge. In these cases, the user can change to the non-true MLE approach (in Weibull++ Application Setup), where <math>\gamma \,\!</math> is estimated using non-linear regression. Once <math>\gamma \,\!</math> is obtained, the MLE estimates of <math>\widehat{\beta }\,\!</math> and <math>\widehat{\eta }\,\!</math> are computed using the transformation <math>T_{i}^{\prime }=({{T}_{i}}-\gamma ).\,\!</math> | ||
| Line 108: | Line 108: | ||
This log-likelihood function is composed of three summation portions: | This log-likelihood function is composed of three summation portions: | ||
::<math>\ln (L)=\Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-\lambda T_{Li}^{\prime \prime }}}-{{e}^{-\lambda T_{Ri}^{\prime \prime }}} \right]</math> | ::<math>\ln (L)=\Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-\lambda T_{Li}^{\prime \prime }}}-{{e}^{-\lambda T_{Ri}^{\prime \prime }}} \right]\,\!</math> | ||
where: | where: | ||
| Line 122: | Line 122: | ||
:*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in the <math>{{i}^{th}}\,\!</math> group of data intervals | :*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in the <math>{{i}^{th}}\,\!</math> group of data intervals | ||
:*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the <math>{{i}^{th}}\,\!</math> interval | :*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the <math>{{i}^{th}}\,\!</math> interval | ||
:*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the | :*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | ||
The solution will be found by solving for a parameter <math>\widehat{\lambda }\,\!</math> so that <math>\tfrac{\partial \Lambda }{\partial \lambda }=0.\,\!</math> Note that for <math>FI=0\,\!</math> there exists a closed form solution. | The solution will be found by solving for a parameter <math>\widehat{\lambda }\,\!</math> so that <math>\tfrac{\partial \Lambda }{\partial \lambda }=0.\,\!</math> Note that for <math>FI=0\,\!</math> there exists a closed form solution. | ||
| Line 129: | Line 129: | ||
\frac{\partial \Lambda }{\partial \lambda }= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{1}{\lambda }-{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }T_{i}^{\prime } \\ | \frac{\partial \Lambda }{\partial \lambda }= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{1}{\lambda }-{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }T_{i}^{\prime } \\ | ||
& -\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\left[ \frac{T_{Li}^{\prime \prime }{{e}^{-\lambda T_{Li}^{\prime \prime }}}-T_{Ri}^{\prime \prime }{{e}^{-\lambda T_{Ri}^{\prime \prime }}}}{{{e}^{-\lambda T_{Li}^{\prime \prime }}}-{{e}^{-\lambda T_{Ri}^{\prime \prime }}}} \right] | & -\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\left[ \frac{T_{Li}^{\prime \prime }{{e}^{-\lambda T_{Li}^{\prime \prime }}}-T_{Ri}^{\prime \prime }{{e}^{-\lambda T_{Ri}^{\prime \prime }}}}{{{e}^{-\lambda T_{Li}^{\prime \prime }}}-{{e}^{-\lambda T_{Ri}^{\prime \prime }}}} \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
==== The Two-Parameter Exponential==== | ==== The Two-Parameter Exponential==== | ||
| Line 138: | Line 138: | ||
& \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda \left( {{T}_{i}}-\gamma \right)}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda \left( T_{i}^{\prime }-\gamma \right) \\ | & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda \left( {{T}_{i}}-\gamma \right)}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda \left( T_{i}^{\prime }-\gamma \right) \\ | ||
& & \ \ +\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-\lambda \left( T_{Li}^{\prime \prime }-\gamma \right)}}-{{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}} \right], | & & \ \ +\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-\lambda \left( T_{Li}^{\prime \prime }-\gamma \right)}}-{{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}} \right], | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
| Line 155: | Line 155: | ||
:*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | :*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | ||
To find the two-parameter solution, look at the partial derivatives <math>\tfrac{\partial \Lambda }{\partial \lambda }</math> and <math>\tfrac{\partial \Lambda }{\partial \gamma}</math>: | |||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 161: | Line 161: | ||
& -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\left( T_{i}^{\prime }-\gamma \right) \\ | & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\left( T_{i}^{\prime }-\gamma \right) \\ | ||
& -\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\left[ \frac{\left( T_{Li}^{\prime \prime }-\gamma \right){{e}^{-\lambda \left( T_{Li}^{\prime \prime }-{{\gamma }_{0}} \right)}}-\left( T_{Ri}^{\prime \prime }-\gamma \right){{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}}}{{{e}^{-\lambda \left( T_{Li}^{\prime \prime }-\gamma \right)}}-{{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}}} \right] | & -\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\left[ \frac{\left( T_{Li}^{\prime \prime }-\gamma \right){{e}^{-\lambda \left( T_{Li}^{\prime \prime }-{{\gamma }_{0}} \right)}}-\left( T_{Ri}^{\prime \prime }-\gamma \right){{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}}}{{{e}^{-\lambda \left( T_{Li}^{\prime \prime }-\gamma \right)}}-{{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}}} \right] | ||
\end{align | \end{align}\,\!</math> | ||
and | |||
::<math>\lambda = | ::<math>\begin{align}\frac{\partial \Lambda }{\partial \gamma }=\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\lambda +\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda +\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\lambda \,\!\end{align}</math>. | ||
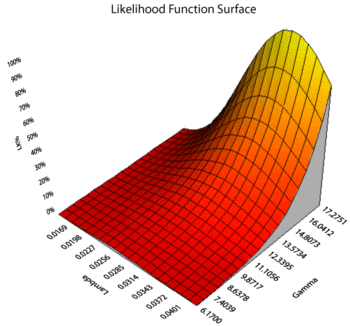
From here we see that <math>\frac{\partial \Lambda }{\partial \gamma}</math> is a positive, constant function of <math>\gamma</math>. As alluded to in the chapter on the exponential distribution, this implies that the log-likelihood function <math>\Lambda</math> is, for fixed <math>\lambda</math>, an increasing function of <math>\gamma</math>. Thus the MLE for <math>\gamma</math> is its largest possible value <math>T_1</math>. Therefore, to find the full MLE solution <math>(\widehat{\lambda },\widehat{\gamma})</math> for the two-parameter exponential distribution, one should set <math>\gamma</math> equal to the first failure time and then find (numerically) a <math>\lambda</math> such that <math>\tfrac{\partial \Lambda}{\partial \lambda} = 0</math>. | |||
The 3D Plot utility in Weibull++ further illustrates this behavior of the log-likelihood function, as shown next: | |||
[[image: appendixc__127.gif|center|350px]] | [[image: appendixc__127.gif|center|350px]] | ||
| Line 194: | Line 181: | ||
& +\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{^{\prime }}\ln \left[ 1-\Phi \left( \frac{T_{i}^{^{\prime }}-\mu }{\sigma } \right) \right] \\ | & +\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{^{\prime }}\ln \left[ 1-\Phi \left( \frac{T_{i}^{^{\prime }}-\mu }{\sigma } \right) \right] \\ | ||
& \text{ }+\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{^{\prime \prime }}\ln \left[ \Phi \left( \frac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma } \right)-\Phi \left( \frac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma } \right) \right] | & \text{ }+\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{^{\prime \prime }}\ln \left[ \Phi \left( \frac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma } \right)-\Phi \left( \frac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma } \right) \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 219: | Line 206: | ||
& +\frac{1}{\sigma }\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)}{1-\Phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)} \\ | & +\frac{1}{\sigma }\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)}{1-\Phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)} \\ | ||
& -\frac{1}{\sigma }\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{\prime \prime }\frac{\phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)}{\Phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\Phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)} | & -\frac{1}{\sigma }\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{\prime \prime }\frac{\phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)}{\Phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\Phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 227: | Line 214: | ||
& +\frac{1}{\sigma }\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)}{1-\Phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)} \\ | & +\frac{1}{\sigma }\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)}{1-\Phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)} \\ | ||
& -\frac{1}{\sigma }\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{\prime \prime }\frac{\left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)}{\Phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\Phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)} | & -\frac{1}{\sigma }\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{\prime \prime }\frac{\left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)}{\Phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\Phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
::<math>\phi \left( x \right)=\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{ | ::<math>\phi \left( x \right)=\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{{{x}^{2}}}{2}}}\,\!</math> | ||
and: | and: | ||
::<math>\Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt</math> | ::<math>\Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt\,\!</math> | ||
| Line 242: | Line 229: | ||
::<math>\widehat{\mu }=\widehat{{\bar{T}}}=\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{T}_{i}}</math> | ::<math>\widehat{\mu }=\widehat{{\bar{T}}}=\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{T}_{i}}\,\!</math> | ||
and: | and: | ||
| Line 249: | Line 236: | ||
\hat{\sigma }_{T}^{2}= & \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \\ | \hat{\sigma }_{T}^{2}= & \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \\ | ||
{{{\hat{\sigma }}}_{T}}= & \sqrt{\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}} | {{{\hat{\sigma }}}_{T}}= & \sqrt{\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
=== Lognormal Log-Likelihood Functions and their Partials=== | === Lognormal Log-Likelihood Functions and their Partials=== | ||
| Line 256: | Line 243: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{\sigma }_{{{T}'}}}}\phi \left( \frac{\ln \left( {{T}_{i}} \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] \\ | \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{T}_{i}} {{\sigma }_{{{T}'}}}}\phi \left( \frac{\ln \left( {{T}_{i}} \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] \\ | ||
& \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] \\ | & \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] \\ | ||
& \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ \Phi \left( \frac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\Phi \left( \frac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] | & \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ \Phi \left( \frac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\Phi \left( \frac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
| Line 277: | Line 264: | ||
The solution will be found by solving for a pair of parameters <math>\left( {\mu }',{{\sigma }_{{{T}'}}} \right)\,\!</math> so that <math>\tfrac{\partial \Lambda }{\partial {\mu }'}=0\,\!</math> and <math>\tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0\,\!</math>: | The solution will be found by solving for a pair of parameters <math>\left( {\mu }',{{\sigma }_{{{T}'}}} \right)\,\!</math> so that <math>\tfrac{\partial \Lambda }{\partial {\mu }'}=0\,\!</math> and <math>\tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0\,\!</math>: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\frac{\partial \Lambda }{\partial {\mu }'}= & \frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\, | \frac{\partial \Lambda }{\partial {\mu }'}= & \frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,N_{i}(\ln ({{T}_{i}})-{\mu }') \\ | ||
& +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} \\ | & +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} \\ | ||
& \ \ -\underset{i=1}{\overset{FI}{\mathop \sum }}\,\frac{N_{i}^{\prime \prime }}{\sigma }\frac{\phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{\Phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\Phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} | & \ \ -\underset{i=1}{\overset{FI}{\mathop \sum }}\,\frac{N_{i}^{\prime \prime }}{\sigma }\frac{\phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{\Phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\Phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
::<math>\begin{align} | |||
\frac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,N_{i}\left( \frac{{{\left( \ln ({{T}_{i}})-{\mu }' \right)}^{2}}}{\sigma _{{{T}'}}^{3}}-\frac{1}{{{\sigma }_{{{T}'}}}} \right) \\ | |||
& +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} \\ | |||
& -\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\frac{\left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{\Phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\Phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} | |||
\end{align}\,\!</math> | |||
where: | where: | ||
::<math>\phi \left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{ | ::<math>\phi \left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{{{x}^{2}}}{2}}}\,\!</math> | ||
and: | and: | ||
::<math>\Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt</math> | ::<math>\Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt\,\!</math> | ||
=== Mixed Weibull Log-Likelihood Functions and their Partials=== | === Mixed Weibull Log-Likelihood Functions and their Partials=== | ||
The log-likelihood function (without the constant) is composed of three summation portions: | The log-likelihood function (without the constant) is composed of three summation portions: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 306: | Line 296: | ||
& \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ \underset{k=1}{\overset{Q}{\mathop \sum }}\,{{\rho }_{k}}{{e}^{-{{\left( \tfrac{T_{i}^{\prime }}{{{\eta }_{k}}} \right)}^{{{\beta }_{k}}}}}} \right] \\ | & \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ \underset{k=1}{\overset{Q}{\mathop \sum }}\,{{\rho }_{k}}{{e}^{-{{\left( \tfrac{T_{i}^{\prime }}{{{\eta }_{k}}} \right)}^{{{\beta }_{k}}}}}} \right] \\ | ||
& \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ \underset{k=1}{\overset{Q}{\mathop \sum }}\,{{\rho }_{k}}\frac{{{\beta }_{k}}}{{{\eta }_{k}}}{{\left( \frac{T_{Li}^{\prime \prime }+T_{Ri}^{\prime \prime }}{2{{\eta }_{k}}} \right)}^{{{\beta }_{k}}-1}}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }+T_{Ri}^{\prime \prime }}{2{{\eta }_{k}}} \right)}^{{{\beta }_{k}}}}}} \right] | & \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ \underset{k=1}{\overset{Q}{\mathop \sum }}\,{{\rho }_{k}}\frac{{{\beta }_{k}}}{{{\eta }_{k}}}{{\left( \frac{T_{Li}^{\prime \prime }+T_{Ri}^{\prime \prime }}{2{{\eta }_{k}}} \right)}^{{{\beta }_{k}}-1}}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }+T_{Ri}^{\prime \prime }}{2{{\eta }_{k}}} \right)}^{{{\beta }_{k}}}}}} \right] | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
| Line 327: | Line 317: | ||
The solution will be found by solving for a group of parameters: | The solution will be found by solving for a group of parameters: | ||
::<math>\left( \widehat{{{\rho }_{1,}}}\widehat{{{\beta }_{1}}},\widehat{{{\eta }_{1}}},\widehat{{{\rho }_{2,}}}\widehat{{{\beta }_{2}}},\widehat{{{\eta }_{2}}},...,\widehat{{{\rho }_{Q,}}}\widehat{{{\beta }_{Q}}},\widehat{{{\eta }_{Q}}} \right)</math> | ::<math>\left( \widehat{{{\rho }_{1,}}}\widehat{{{\beta }_{1}}},\widehat{{{\eta }_{1}}},\widehat{{{\rho }_{2,}}}\widehat{{{\beta }_{2}}},\widehat{{{\eta }_{2}}},...,\widehat{{{\rho }_{Q,}}}\widehat{{{\beta }_{Q}}},\widehat{{{\eta }_{Q}}} \right)\,\!</math> | ||
so that: | so that: | ||
| Line 337: | Line 327: | ||
\frac{\partial \Lambda }{\partial {{\rho }_{Q-1}}}= & 0,\frac{\partial \Lambda }{\partial {{\beta }_{Q-1}}}=0,\frac{\partial \Lambda }{\partial {{\eta }_{Q-1}}}=0 \\ | \frac{\partial \Lambda }{\partial {{\rho }_{Q-1}}}= & 0,\frac{\partial \Lambda }{\partial {{\beta }_{Q-1}}}=0,\frac{\partial \Lambda }{\partial {{\eta }_{Q-1}}}=0 \\ | ||
\frac{\partial \Lambda }{\partial {{\beta }_{Q}}}= & 0,\text{ and }\frac{\partial \Lambda }{\partial {{\eta }_{Q}}}=0 | \frac{\partial \Lambda }{\partial {{\beta }_{Q}}}= & 0,\text{ and }\frac{\partial \Lambda }{\partial {{\eta }_{Q}}}=0 | ||
\end{align}</math> | \end{align}\,\!</math> | ||
=== Logistic Log-Likelihood Functions and their Partials=== | === Logistic Log-Likelihood Functions and their Partials=== | ||
| Line 345: | Line 335: | ||
\ln (L)= & \Lambda =\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln \left( \frac{{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}{\sigma {{(1+{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}})}^{2}}} \right)-\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln (1+{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}) \\ | \ln (L)= & \Lambda =\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln \left( \frac{{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}{\sigma {{(1+{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}})}^{2}}} \right)-\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln (1+{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}) \\ | ||
& +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( \frac{1}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}-\frac{1}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \right) | & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( \frac{1}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}-\frac{1}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
| Line 359: | Line 349: | ||
:*<math>FI\,\!</math> is the number of interval failure data group | :*<math>FI\,\!</math> is the number of interval failure data group | ||
:*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in <math>{{i}^{th}}\,\!</math> group of data intervals | :*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in <math>{{i}^{th}}\,\!</math> group of data intervals | ||
:*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the | :*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the <math>{{i}^{th}}\,\!</math> interval | ||
:*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the | :*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | ||
For the purposes of MLE, left censored data will be considered to be intervals with <math>T_{Li}^{\prime \prime }=0.\,\!</math> | For the purposes of MLE, left censored data will be considered to be intervals with <math>T_{Li}^{\prime \prime }=0.\,\!</math> | ||
| Line 370: | Line 360: | ||
\frac{\partial \Lambda }{\partial \mu }= & -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\frac{2}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}} \\ | \frac{\partial \Lambda }{\partial \mu }= & -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\frac{2}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}} \\ | ||
& -\frac{\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\mathop{}_{}^{}}}\,}}\,N_{i}^{^{\prime \prime }}}{\sigma }+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}+\frac{{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \right) | & -\frac{\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\mathop{}_{}^{}}}\,}}\,N_{i}^{^{\prime \prime }}}{\sigma }+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}+\frac{{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 380: | Line 370: | ||
& \frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}(\frac{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}+\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \\ | & \frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}(\frac{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}+\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \\ | ||
& -\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}-\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}) | & -\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}-\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
=== The Loglogistic Log-Likelihood Functions and their Partials=== | === The Loglogistic Log-Likelihood Functions and their Partials=== | ||
| Line 389: | Line 379: | ||
& -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln (1+{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}) \\ | & -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln (1+{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}) \\ | ||
& +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( \frac{1}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}-\frac{1}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \right) | & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( \frac{1}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}-\frac{1}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
:*<math>{{F}_{e}}</math> is the number of groups of times-to-failure data points | :*<math>{{F}_{e}}\,\!</math> is the number of groups of times-to-failure data points | ||
:*<math>{{N}_{i}}</math> is the number of times-to-failure in the <math>{{i}^{th}}</math> time-to-failure data group | :*<math>{{N}_{i}}\,\!</math> is the number of times-to-failure in the <math>{{i}^{th}}\,\!</math> time-to-failure data group | ||
:*<math>\mu </math> is the loglogistic shape parameter (unknown a priori, the first of two parameters to be found) | :*<math>\mu \,\!</math> is the loglogistic shape parameter (unknown a priori, the first of two parameters to be found) | ||
:*<math>\sigma </math> is the loglogistic scale parameter (unknown a priori, the second of two parameters to be found) | :*<math>\sigma \,\!</math> is the loglogistic scale parameter (unknown a priori, the second of two parameters to be found) | ||
:*<math>{{T}_{i}}</math> is the time of the <math>{{i}^{th}}</math> group of time-to-failure data | :*<math>{{T}_{i}}\,\!</math> is the time of the <math>{{i}^{th}}\,\!</math> group of time-to-failure data | ||
:*<math>S</math> is the number of groups of suspension data points | :*<math>S\,\!</math> is the number of groups of suspension data points | ||
:*<math>N_{i}^{\prime }</math> is the number of suspensions in <math>{{i}^{th}}</math> group of suspension data points | :*<math>N_{i}^{\prime }\,\!</math> is the number of suspensions in <math>{{i}^{th}}\,\!</math> group of suspension data points | ||
:*<math>T_{i}^{\prime }</math> is the time of the <math>{{i}^{th}}</math> suspension data group | :*<math>T_{i}^{\prime }\,\!</math> is the time of the <math>{{i}^{th}}\,\!</math> suspension data group | ||
:*<math>FI</math> is the number of interval failure data groups, | :*<math>FI\,\!</math> is the number of interval failure data groups, | ||
:*<math>N_{i}^{\prime \prime }</math> is the number of intervals in <math>{{i}^{th}}</math> group of data intervals | :*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in <math>{{i}^{th}}\,\!</math> group of data intervals | ||
:*<math>T_{Li}^{\prime \prime }</math> is the beginning of the <math>{{i}^{th}}</math> interval | :*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the <math>{{i}^{th}}\,\!</math> interval | ||
:*<math>T_{Ri}^{\prime \prime }</math> is the ending of the <math>{{i}^{th}}</math> interval | :*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | ||
For the purposes of MLE, left censored data will be considered to be intervals with <math>T_{Li}^{\prime \prime }=0.</math> | For the purposes of MLE, left censored data will be considered to be intervals with <math>T_{Li}^{\prime \prime }=0.\,\!</math> | ||
The solution of the maximum log-likelihood function is found by solving for (<math>\widehat{\mu },\widehat{\sigma })</math> so that <math>\tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial \sigma }=0.</math> | The solution of the maximum log-likelihood function is found by solving for (<math>\widehat{\mu },\widehat{\sigma })\,\!</math> so that <math>\tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial \sigma }=0.\,\!</math> | ||
| Line 415: | Line 405: | ||
& +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}}-\frac{{{F}_{I}}}{\sigma } \\ | & +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}}-\frac{{{F}_{I}}}{\sigma } \\ | ||
& +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}+\frac{{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \right) | & +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}+\frac{{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 424: | Line 414: | ||
& \frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}(\frac{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}+\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \\ | & \frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}(\frac{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}+\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \\ | ||
& -\frac{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}-\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}-{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}) | & -\frac{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}-\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}-{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
=== The Gumbel Log-Likelihood Functions and their Partials=== | === The Gumbel Log-Likelihood Functions and their Partials=== | ||
| Line 433: | Line 423: | ||
& -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}}} \right) \\ | & -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}}} \right) \\ | ||
& +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}} \right) | & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
or: | or: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 443: | Line 431: | ||
& +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}} \\ | & +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}} \\ | ||
& +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}} \right) | & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
:*<math>{{F}_{e}}</math> is the number of groups of times-to-failure data points | :*<math>{{F}_{e}}\,\!</math> is the number of groups of times-to-failure data points | ||
:*<math>{{N}_{i}}</math> is the number of times-to-failure in the | :*<math>{{N}_{i}}\,\!</math> is the number of times-to-failure in the <math>{{i}^{th}}\,\!</math> time-to-failure data group | ||
:*<math>\mu </math> is the Gumbel shape parameter (unknown a priori, the first of two parameters to be found) | :*<math>\mu \,\!</math> is the Gumbel shape parameter (unknown a priori, the first of two parameters to be found) | ||
:*<math>\sigma </math> is the Gumbel scale parameter (unknown a priori, the second of two parameters to be found) | :*<math>\sigma \,\!</math> is the Gumbel scale parameter (unknown a priori, the second of two parameters to be found) | ||
:*<math>{{T}_{i}}</math> is the time of the <math>{{i}^{th}}</math> group of time-to-failure data | :*<math>{{T}_{i}}\,\!</math> is the time of the <math>{{i}^{th}}\,\!</math> group of time-to-failure data | ||
:*<math>S</math> is the number of groups of suspension data points | :*<math>S\,\!</math> is the number of groups of suspension data points | ||
:*<math>N_{i}^{\prime }</math> is the number of suspensions in <math>{{i}^{th}}</math> group of suspension data points | :*<math>N_{i}^{\prime }\,\!</math> is the number of suspensions in <math>{{i}^{th}}\,\!</math> group of suspension data points | ||
:*<math>T_{i}^{\prime }</math> is the time of the <math>{{i}^{th}}</math> | :*<math>T_{i}^{\prime }\,\!</math> is the time of the <math>{{i}^{th}}\,\!</math> suspension data group | ||
:*<math>FI</math> is the number of interval failure data groups | :*<math>FI\,\!</math> is the number of interval failure data groups | ||
:*<math>N_{i}^{\prime \prime }</math> is the number of intervals in <math>{{i}^{th}}</math> group of data intervals | :*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in <math>{{i}^{th}}\,\!</math> group of data intervals | ||
:*<math>T_{Li}^{\prime \prime }</math> is the beginning of the <math>{{i}^{th}}</math> interval | :*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the <math>{{i}^{th}}\,\!</math> interval | ||
:*<math>T_{Ri}^{\prime \prime }</math> is the ending of the <math>{{i}^{th}}</math> interval | :*<math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | ||
For the purposes of MLE, left censored data will be considered to be intervals with <math>T_{Li}^{\prime \prime }=0.</math> | For the purposes of MLE, left censored data will be considered to be intervals with <math>T_{Li}^{\prime \prime }=0.\,\!</math> | ||
The solution of the maximum log-likelihood function is found by solving for (<math>\widehat{\mu },\widehat{\sigma })</math> so that: | The solution of the maximum log-likelihood function is found by solving for (<math>\widehat{\mu },\widehat{\sigma })\,\!</math> so that: | ||
::<math>\tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial \sigma }=0.</math> | ::<math>\tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial \sigma }=0.\,\!</math> | ||
| Line 470: | Line 458: | ||
\frac{\partial \Lambda }{\partial \mu }= & -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}-\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}} \\ | \frac{\partial \Lambda }{\partial \mu }= & -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}-\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}} \\ | ||
& +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}}{{{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}} \right) | & +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}}{{{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 479: | Line 466: | ||
& -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{T_{i}^{^{\prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }} \\ | & -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{T_{i}^{^{\prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }} \\ | ||
& \left( \frac{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}}{{{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}} \right) | & \left( \frac{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}}{{{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
=== The Gamma Log-Likelihood Functions and their Partials=== | === The Gamma Log-Likelihood Functions and their Partials=== | ||
| Line 488: | Line 475: | ||
& +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( 1-\Gamma \left( _{1}k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu )}} \right) \right) \\ | & +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( 1-\Gamma \left( _{1}k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu )}} \right) \right) \\ | ||
& +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right) \right) | & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right) \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
or: | or: | ||
| Line 497: | Line 484: | ||
& +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( 1-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }} \right) \right) \\ | & +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( 1-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }} \right) \right) \\ | ||
& +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu )}} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu )}} \right) \right) | & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu )}} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu )}} \right) \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
:*<math>{{F}_{e}}</math> is the number of groups of times-to-failure data points | :*<math>{{F}_{e}}\,\!</math> is the number of groups of times-to-failure data points | ||
:*<math>{{N}_{i}}</math> is the number of times-to-failure in the <math>{{i}^{th}}</math> time-to-failure data group | :*<math>{{N}_{i}}\,\!</math> is the number of times-to-failure in the <math>{{i}^{th}}\,\!</math> time-to-failure data group | ||
:*<math>\mu </math> is the gamma shape parameter (unknown a priori, the first of two parameters to be found) | :*<math>\mu \,\!</math> is the gamma shape parameter (unknown a priori, the first of two parameters to be found) | ||
:*<math>k</math> is the gamma scale parameter (unknown a priori, the second of two parameters to be found) | :*<math>k\,\!</math> is the gamma scale parameter (unknown a priori, the second of two parameters to be found) | ||
:*<math>{{T}_{i}}</math> is the time of the <math>{{i}^{th}}</math> group of time-to-failure data | :*<math>{{T}_{i}}\,\!</math> is the time of the <math>{{i}^{th}}\,\!</math> group of time-to-failure data | ||
:*<math>S</math> is the number of groups of suspension data points | :*<math>S\,\!</math> is the number of groups of suspension data points | ||
:*<math>N_{i}^{\prime }</math> is the number of suspensions in <math>{{i}^{th}}</math> group of suspension data points | :*<math>N_{i}^{\prime }\,\!</math> is the number of suspensions in <math>{{i}^{th}}\,\!</math> group of suspension data points | ||
:*<math>T_{i}^{\prime }</math> is the time of the <math>{{i}^{th}}</math> suspension data group | :*<math>T_{i}^{\prime }\,\!</math> is the time of the <math>{{i}^{th}}\,\!</math> suspension data group | ||
:*<math>FI</math> is the number of interval failure data groups | :*<math>FI\,\!</math> is the number of interval failure data groups | ||
:*<math>N_{i}^{\prime \prime }</math> is the number of intervals in <math>{{i}^{th}}</math> group of data intervals | :*<math>N_{i}^{\prime \prime }\,\!</math> is the number of intervals in <math>{{i}^{th}}\,\!</math> group of data intervals | ||
:*<math>T_{Li}^{\prime \prime }</math> is the beginning of the <math>{{i}^{th}}</math> interval | :*<math>T_{Li}^{\prime \prime }\,\!</math> is the beginning of the <math>{{i}^{th}}\,\!</math> interval | ||
:*and <math>T_{Ri}^{\prime \prime }</math> is the ending of the <math>{{i}^{th}}</math> interval | :*and <math>T_{Ri}^{\prime \prime }\,\!</math> is the ending of the <math>{{i}^{th}}\,\!</math> interval | ||
For the purposes of MLE, left censored data will be considered to be intervals with <math>T_{Li}^{\prime \prime }=0.</math> | For the purposes of MLE, left censored data will be considered to be intervals with <math>T_{Li}^{\prime \prime }=0.\,\!</math> | ||
The solution of the maximum log-likelihood function is found by solving for (<math>\widehat{\mu },\widehat{\sigma })</math> so that <math>\tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial k}=0.</math> | The solution of the maximum log-likelihood function is found by solving for (<math>\widehat{\mu },\widehat{\sigma })\,\!</math> so that <math>\tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial k}=0.\,\!</math> | ||
| Line 524: | Line 511: | ||
& +\frac{1}{\Gamma (k)}\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\{\frac{{{e}^{k{{e}^{{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }}}}-{{e}^{{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }}}}}}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)} \\ | & +\frac{1}{\Gamma (k)}\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\{\frac{{{e}^{k{{e}^{{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }}}}-{{e}^{{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }}}}}}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)} \\ | ||
& -\frac{{{e}^{k{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}-{{e}^{{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}}}}}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)}\} | & -\frac{{{e}^{k{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}-{{e}^{{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}}}}}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)}\} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
| Line 533: | Line 520: | ||
& -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{\tfrac{\partial {{\Gamma }_{1}}(k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }})}{\partial k}}{1-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }} \right)} \\ | & -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{\tfrac{\partial {{\Gamma }_{1}}(k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }})}{\partial k}}{1-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }} \right)} \\ | ||
& +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{\tfrac{\partial {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)}{\partial k}-\tfrac{\partial {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)}{\partial k}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}) \right)} \right) | & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{\tfrac{\partial {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)}{\partial k}-\tfrac{\partial {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)}{\partial k}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}) \right)} \right) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Latest revision as of 19:13, 15 September 2023
This appendix covers the log-likelihood functions and their associated partial derivatives for most of the distributions available in Weibull++. These distributions are discussed in more detail in the chapter for each distribution.
Weibull Log-Likelihood Functions and their Partials
The Two-Parameter Weibull
This log-likelihood function is composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{{{T}_{i}}}{\eta } \right)}^{\beta }}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }} \\ & \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}} \right] \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \beta \,\! }[/math] is the Weibull shape parameter (unknown a priori, the first of two parameters to be found)
- [math]\displaystyle{ \eta \,\! }[/math] is the Weibull scale parameter (unknown a priori, the second of two parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval failure data groups
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
For the purposes of MLE, left censored data will be considered to be intervals with [math]\displaystyle{ T_{Li}^{\prime \prime }=0.\,\! }[/math]
The solution will be found by solving for a pair of parameters [math]\displaystyle{ \left( \widehat{\beta },\widehat{\eta } \right)\,\! }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \beta }=0\,\! }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \eta }=0.\,\! }[/math] It should be noted that other methods can also be used, such as direct maximization of the likelihood function, without having to compute the derivatives.
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \beta }= & \frac{1}{\beta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}+\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\ln \left( \frac{{{T}_{i}}}{\eta } \right) \\ & -\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta }}\ln \left( \frac{{{T}_{i}}}{\eta } \right)-\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }}\ln \left( \frac{T_{i}^{\prime }}{\eta } \right) \\ & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}+{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}} \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \eta }= & \frac{-\beta }{\eta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}+\frac{\beta }{\eta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta }} \\ & +\frac{\beta }{\eta }\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }}{\eta } \right)}^{\beta }} \\ & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\left( \tfrac{\beta }{\eta } \right){{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-\left( \tfrac{\beta }{\eta } \right){{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }}{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }}{\eta } \right)}^{\beta }}}}} \end{align}\,\! }[/math]
The Three-Parameter Weibull
This log-likelihood function is again composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}-\gamma }{\eta } \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{{{T}_{i}}-\gamma }{\eta } \right)}^{\beta }}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }-\gamma }{\eta } \right)}^{\beta }} \\ & \\ & +\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}} \right] \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \beta \,\! }[/math] is the Weibull shape parameter (unknown a priori, the first of three parameters to be found)
- [math]\displaystyle{ \eta \,\! }[/math] is the Weibull scale parameter (unknown a priori, the second of three parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ \gamma \,\! }[/math] is the Weibull location parameter (unknown a priori, the third of three parameters to be found)
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval data groups
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- and [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
The solution is found by solving for [math]\displaystyle{ \left( \widehat{\beta },\widehat{\eta },\widehat{\gamma } \right)\,\! }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \beta }=0,\,\! }[/math] [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \eta }=0,\,\! }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \gamma }=0.\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \beta }= & \frac{1}{\beta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}+\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}\ln \left( \frac{{{T}_{i}}-\gamma }{\eta } \right)-\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}-\gamma }{\eta } \right)}^{\beta }}\ln \left( \frac{{{T}_{i}}-\gamma }{\eta } \right) \\ & -\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \frac{T_{i}^{\prime }-\gamma }{\eta } \right) \\ & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \\ & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \eta }= & \frac{-\beta }{\eta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}+\frac{\beta }{\eta }\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}-\gamma }{\eta } \right)}^{\beta }}+\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }-\gamma }{\eta } \right)}^{\beta }}\left( \frac{\beta }{\eta } \right) \\ & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{\eta }{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \\ & -\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{\eta }{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}\ln \left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right){{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \gamma }= & \left( 1-\beta \right)\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,\left( \frac{{{N}_{i}}}{{{T}_{i}}-\gamma } \right)+\underset{i=1}{\overset{{{F}_{e}}}{\mathop{\sum }}}\,{{N}_{i}}{{\left( \frac{{{T}_{i}}-\gamma }{\eta } \right)}^{\beta }}\left( \frac{\beta }{{{T}_{i}}-\gamma } \right) \\ & +\underset{i=1}{\overset{S}{\mathop{\sum }}}\,N_{i}^{\prime }{{\left( \frac{T_{i}^{\prime }-\gamma }{\eta } \right)}^{\beta }}\left( \frac{\beta }{T_{i}^{\prime }-\gamma } \right) \\ & +\underset{i=1}{\overset{FI}{\mathop{\sum }}}\,N_{i}^{\prime \prime }\frac{\tfrac{\beta }{T_{Li}^{\prime \prime }-\gamma }{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-\tfrac{\beta }{T_{Ri}^{\prime \prime }-\gamma }{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}}{{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}-{{e}^{-{{\left( \tfrac{T_{Ri}^{\prime \prime }-\gamma }{\eta } \right)}^{\beta }}}}} \end{align}\,\! }[/math]
It should be pointed out that the solution to the three-parameter Weibull via MLE is not always stable and can collapse if [math]\displaystyle{ \beta \sim 1.\,\! }[/math] In estimating the true MLE of the three-parameter Weibull distribution, two difficulties arise. The first is a problem of non-regularity and the second is the parameter divergence problem, as discussed in Hirose [14].
Non-regularity occurs when [math]\displaystyle{ \beta \le 2.\,\! }[/math] In general, there are no MLE solutions in the region of [math]\displaystyle{ 0\lt \beta \lt 1.\,\! }[/math] When [math]\displaystyle{ 1\lt \beta \lt 2,\,\! }[/math] MLE solutions exist but are not asymptotically normal, as discussed in Hirose [14]. In the case of non-regularity, the solution is treated anomalously.
Weibull++ attempts to find a solution in all of the regions using a variety of methods, but the user should be forewarned that not all possible data can be addressed. Thus, some solutions using MLE for the three-parameter Weibull will fail when the algorithm has reached predefined limits or fails to converge. In these cases, the user can change to the non-true MLE approach (in Weibull++ Application Setup), where [math]\displaystyle{ \gamma \,\! }[/math] is estimated using non-linear regression. Once [math]\displaystyle{ \gamma \,\! }[/math] is obtained, the MLE estimates of [math]\displaystyle{ \widehat{\beta }\,\! }[/math] and [math]\displaystyle{ \widehat{\eta }\,\! }[/math] are computed using the transformation [math]\displaystyle{ T_{i}^{\prime }=({{T}_{i}}-\gamma ).\,\! }[/math]
Exponential Log-Likelihood Functions and their Partials
The One-Parameter Exponential
This log-likelihood function is composed of three summation portions:
- [math]\displaystyle{ \ln (L)=\Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-\lambda T_{Li}^{\prime \prime }}}-{{e}^{-\lambda T_{Ri}^{\prime \prime }}} \right]\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \lambda \,\! }[/math] is the failure rate parameter (unknown a priori, the only parameter to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval data groups
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
The solution will be found by solving for a parameter [math]\displaystyle{ \widehat{\lambda }\,\! }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \lambda }=0.\,\! }[/math] Note that for [math]\displaystyle{ FI=0\,\! }[/math] there exists a closed form solution.
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \lambda }= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{1}{\lambda }-{{T}_{i}} \right)-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }T_{i}^{\prime } \\ & -\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\left[ \frac{T_{Li}^{\prime \prime }{{e}^{-\lambda T_{Li}^{\prime \prime }}}-T_{Ri}^{\prime \prime }{{e}^{-\lambda T_{Ri}^{\prime \prime }}}}{{{e}^{-\lambda T_{Li}^{\prime \prime }}}-{{e}^{-\lambda T_{Ri}^{\prime \prime }}}} \right] \end{align}\,\! }[/math]
The Two-Parameter Exponential
This log-likelihood function for the two-parameter exponential distribution is very similar to that of the one-parameter distribution and is composed of three summation portions:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda \left( {{T}_{i}}-\gamma \right)}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda \left( T_{i}^{\prime }-\gamma \right) \\ & & \ \ +\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ {{e}^{-\lambda \left( T_{Li}^{\prime \prime }-\gamma \right)}}-{{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}} \right], \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \lambda \,\! }[/math] is the failure rate parameter (unknown a priori, the first of two parameters to be found)
- [math]\displaystyle{ \gamma \,\! }[/math] is the location parameter (unknown a priori, the second of two parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval data groups
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
To find the two-parameter solution, look at the partial derivatives [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \lambda } }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \gamma} }[/math]:
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \lambda }= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left[ \frac{1}{\lambda }-\left( {{T}_{i}}-\gamma \right) \right] \\ & -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\left( T_{i}^{\prime }-\gamma \right) \\ & -\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\left[ \frac{\left( T_{Li}^{\prime \prime }-\gamma \right){{e}^{-\lambda \left( T_{Li}^{\prime \prime }-{{\gamma }_{0}} \right)}}-\left( T_{Ri}^{\prime \prime }-\gamma \right){{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}}}{{{e}^{-\lambda \left( T_{Li}^{\prime \prime }-\gamma \right)}}-{{e}^{-\lambda \left( T_{Ri}^{\prime \prime }-\gamma \right)}}} \right] \end{align}\,\! }[/math]
and
- [math]\displaystyle{ \begin{align}\frac{\partial \Lambda }{\partial \gamma }=\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\lambda +\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda +\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\lambda \,\!\end{align} }[/math].
From here we see that [math]\displaystyle{ \frac{\partial \Lambda }{\partial \gamma} }[/math] is a positive, constant function of [math]\displaystyle{ \gamma }[/math]. As alluded to in the chapter on the exponential distribution, this implies that the log-likelihood function [math]\displaystyle{ \Lambda }[/math] is, for fixed [math]\displaystyle{ \lambda }[/math], an increasing function of [math]\displaystyle{ \gamma }[/math]. Thus the MLE for [math]\displaystyle{ \gamma }[/math] is its largest possible value [math]\displaystyle{ T_1 }[/math]. Therefore, to find the full MLE solution [math]\displaystyle{ (\widehat{\lambda },\widehat{\gamma}) }[/math] for the two-parameter exponential distribution, one should set [math]\displaystyle{ \gamma }[/math] equal to the first failure time and then find (numerically) a [math]\displaystyle{ \lambda }[/math] such that [math]\displaystyle{ \tfrac{\partial \Lambda}{\partial \lambda} = 0 }[/math].
The 3D Plot utility in Weibull++ further illustrates this behavior of the log-likelihood function, as shown next:
Normal Log-Likelihood Functions and their Partials
The complete normal likelihood function (without the constant) is composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{\sigma }\phi \left( \frac{{{T}_{i}}-\mu }{\sigma } \right) \right] \\ & +\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{^{\prime }}\ln \left[ 1-\Phi \left( \frac{T_{i}^{^{\prime }}-\mu }{\sigma } \right) \right] \\ & \text{ }+\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{^{\prime \prime }}\ln \left[ \Phi \left( \frac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma } \right)-\Phi \left( \frac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma } \right) \right] \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \mu \,\! }[/math] is the mean parameter (unknown a priori, the first of two parameters to be found)
- [math]\displaystyle{ \sigma \,\! }[/math] is the standard deviation parameter (unknown a priori, the second of two parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ {{F}_{i}}\,\! }[/math] is the number of interval data groups
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
The solution will be found by solving for a pair of parameters [math]\displaystyle{ \left( {{\mu }_{0}},{{\sigma }_{0}} \right)\,\! }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \mu }=0\,\! }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \sigma }=0.\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \mu }= & \frac{1}{{{\sigma }^{2}}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}({{T}_{i}}-\mu ) \\ & +\frac{1}{\sigma }\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)}{1-\Phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)} \\ & -\frac{1}{\sigma }\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{\prime \prime }\frac{\phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)}{\Phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\Phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)} \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \sigma }= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{\left( {{T}_{i}}-\mu \right)}^{2}}}{{{\sigma }^{3}}}-\frac{1}{\sigma } \right) \\ & +\frac{1}{\sigma }\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)}{1-\Phi \left( \tfrac{T_{i}^{\prime }-\mu }{\sigma } \right)} \\ & -\frac{1}{\sigma }\underset{i=1}{\overset{{{F}_{i}}}{\mathop \sum }}\,N_{i}^{\prime \prime }\frac{\left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)\phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)}{\Phi \left( \tfrac{T_{Ri}^{\prime \prime }-\mu }{\sigma } \right)-\Phi \left( \tfrac{T_{Li}^{\prime \prime }-\mu }{\sigma } \right)} \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ \phi \left( x \right)=\frac{1}{\sqrt{2\pi }}{{e}^{-\tfrac{{{x}^{2}}}{2}}}\,\! }[/math]
and:
- [math]\displaystyle{ \Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt\,\! }[/math]
Complete Data
Note that for the normal distribution, and in the case of complete data only (as was shown in Basic Statistical Background), there exists a closed-form solution for both of the parameters or:
- [math]\displaystyle{ \widehat{\mu }=\widehat{{\bar{T}}}=\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{T}_{i}}\,\! }[/math]
and:
- [math]\displaystyle{ \begin{align} \hat{\sigma }_{T}^{2}= & \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}} \\ {{{\hat{\sigma }}}_{T}}= & \sqrt{\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{T}_{i}}-\bar{T})}^{2}}} \end{align}\,\! }[/math]
Lognormal Log-Likelihood Functions and their Partials
The general log-likelihood function (without the constant) for the lognormal distribution is composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{{{T}_{i}} {{\sigma }_{{{T}'}}}}\phi \left( \frac{\ln \left( {{T}_{i}} \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] \\ & \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ 1-\Phi \left( \frac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] \\ & \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ \Phi \left( \frac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\Phi \left( \frac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right) \right] \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ {\mu }'\,\! }[/math] is the mean of the natural logarithms of the times-to-failure (unknown a priori, the first of two parameters to be found)
- [math]\displaystyle{ {{\sigma }_{{{T}'}}}\,\! }[/math] is the standard deviation of the natural logarithms of the times-to-failure (unknown a priori, the second of two parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval data groups
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
The solution will be found by solving for a pair of parameters [math]\displaystyle{ \left( {\mu }',{{\sigma }_{{{T}'}}} \right)\,\! }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial {\mu }'}=0\,\! }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}=0\,\! }[/math]:
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial {\mu }'}= & \frac{1}{\sigma _{{{T}'}}^{2}}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,N_{i}(\ln ({{T}_{i}})-{\mu }') \\ & +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} \\ & \ \ -\underset{i=1}{\overset{FI}{\mathop \sum }}\,\frac{N_{i}^{\prime \prime }}{\sigma }\frac{\phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{\Phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\Phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial {{\sigma }_{{{T}'}}}}= & \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,N_{i}\left( \frac{{{\left( \ln ({{T}_{i}})-{\mu }' \right)}^{2}}}{\sigma _{{{T}'}}^{3}}-\frac{1}{{{\sigma }_{{{T}'}}}} \right) \\ & +\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{\left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{1-\Phi \left( \tfrac{\ln \left( T_{i}^{\prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} \\ & -\frac{1}{{{\sigma }_{{{T}'}}}}\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\frac{\left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)\phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)}{\Phi \left( \tfrac{\ln \left( T_{Ri}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)-\Phi \left( \tfrac{\ln \left( T_{Li}^{\prime \prime } \right)-{\mu }'}{{{\sigma }_{{{T}'}}}} \right)} \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ \phi \left( x \right)=\frac{1}{\sqrt{2\pi }}\cdot {{e}^{-\tfrac{{{x}^{2}}}{2}}}\,\! }[/math]
and:
- [math]\displaystyle{ \Phi (x)=\frac{1}{\sqrt{2\pi }}\int_{-\infty }^{x}{{e}^{-\tfrac{{{t}^{2}}}{2}}}dt\,\! }[/math]
Mixed Weibull Log-Likelihood Functions and their Partials
The log-likelihood function (without the constant) is composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \underset{k=1}{\overset{Q}{\mathop \sum }}\,{{\rho }_{k}}\frac{{{\beta }_{k}}}{{{\eta }_{k}}}{{\left( \frac{{{T}_{i}}}{{{\eta }_{k}}} \right)}^{{{\beta }_{k}}-1}}{{e}^{-{{\left( \tfrac{{{T}_{i}}}{{{\eta }_{k}}} \right)}^{{{\beta }_{k}}}}}} \right] \\ & \text{ }+\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\ln \left[ \underset{k=1}{\overset{Q}{\mathop \sum }}\,{{\rho }_{k}}{{e}^{-{{\left( \tfrac{T_{i}^{\prime }}{{{\eta }_{k}}} \right)}^{{{\beta }_{k}}}}}} \right] \\ & \text{ }+\underset{i=1}{\overset{FI}{\mathop \sum }}\,N_{i}^{\prime \prime }\ln \left[ \underset{k=1}{\overset{Q}{\mathop \sum }}\,{{\rho }_{k}}\frac{{{\beta }_{k}}}{{{\eta }_{k}}}{{\left( \frac{T_{Li}^{\prime \prime }+T_{Ri}^{\prime \prime }}{2{{\eta }_{k}}} \right)}^{{{\beta }_{k}}-1}}{{e}^{-{{\left( \tfrac{T_{Li}^{\prime \prime }+T_{Ri}^{\prime \prime }}{2{{\eta }_{k}}} \right)}^{{{\beta }_{k}}}}}} \right] \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ Q\,\! }[/math] is the number of subpopulations
- [math]\displaystyle{ {{\rho }_{k}}\,\! }[/math] is the proportionality of the [math]\displaystyle{ {{k}^{th}}\,\! }[/math] subpopulation (unknown a priori, the first set of three sets of parameters to be found)
- [math]\displaystyle{ {{\beta }_{k}}\,\! }[/math] is the Weibull shape parameter of the [math]\displaystyle{ {{k}^{th}}\,\! }[/math] subpopulation (unknown a priori, the second set of three sets of parameters to be found)
- [math]\displaystyle{ {{\eta }_{k}}\,\! }[/math] is the Weibull scale parameter (unknown a priori, the third set of three sets of parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of groups of interval data points
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
The solution will be found by solving for a group of parameters:
- [math]\displaystyle{ \left( \widehat{{{\rho }_{1,}}}\widehat{{{\beta }_{1}}},\widehat{{{\eta }_{1}}},\widehat{{{\rho }_{2,}}}\widehat{{{\beta }_{2}}},\widehat{{{\eta }_{2}}},...,\widehat{{{\rho }_{Q,}}}\widehat{{{\beta }_{Q}}},\widehat{{{\eta }_{Q}}} \right)\,\! }[/math]
so that:
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial {{\rho }_{1}}}= & 0,\frac{\partial \Lambda }{\partial {{\beta }_{1}}}=0,\frac{\partial \Lambda }{\partial {{\eta }_{1}}}=0 \\ \frac{\partial \Lambda }{\partial {{\rho }_{2}}}= & 0,\frac{\partial \Lambda }{\partial {{\beta }_{2}}}=0,\frac{\partial \Lambda }{\partial {{\eta }_{2}}}=0 \\ \vdots \\ \frac{\partial \Lambda }{\partial {{\rho }_{Q-1}}}= & 0,\frac{\partial \Lambda }{\partial {{\beta }_{Q-1}}}=0,\frac{\partial \Lambda }{\partial {{\eta }_{Q-1}}}=0 \\ \frac{\partial \Lambda }{\partial {{\beta }_{Q}}}= & 0,\text{ and }\frac{\partial \Lambda }{\partial {{\eta }_{Q}}}=0 \end{align}\,\! }[/math]
Logistic Log-Likelihood Functions and their Partials
This log-likelihood function is composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln \left( \frac{{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}{\sigma {{(1+{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}})}^{2}}} \right)-\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln (1+{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}) \\ & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( \frac{1}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}-\frac{1}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \right) \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \mu \,\! }[/math] is the logistic shape parameter (unknown a priori, the first of two parameters to be found)
- [math]\displaystyle{ \eta \,\! }[/math] is the logistic scale parameter (unknown a priori, the second of two parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval failure data group
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
For the purposes of MLE, left censored data will be considered to be intervals with [math]\displaystyle{ T_{Li}^{\prime \prime }=0.\,\! }[/math]
The solution of the maximum log-likelihood function is found by solving for ([math]\displaystyle{ \widehat{\mu },\widehat{\sigma })\,\! }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial \sigma }=0.\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \mu }= & -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\frac{2}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}} \\ & -\frac{\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\mathop{}_{}^{}}}\,}}\,N_{i}^{^{\prime \prime }}}{\sigma }+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}+\frac{{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \right) \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \sigma }= & -\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{{{T}_{i}}-\mu }{{{\sigma }^{2}}}-\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\frac{2}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{\tfrac{{{T}_{i}}-\mu }{\sigma }{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}} \\ & +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}} \\ & \frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}(\frac{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}+\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{1+{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}} \\ & -\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}-\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}{{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}) \end{align}\,\! }[/math]
The Loglogistic Log-Likelihood Functions and their Partials
This log-likelihood function is composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln \left( \frac{{{e}^{\tfrac{\ln ({{T}_{i}})-\mu }{\sigma }}}}{\sigma t{{(1+{{e}^{\tfrac{\ln ({{T}_{i}})-\mu }{\sigma }}})}^{2}}} \right) \\ & -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln (1+{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}) \\ & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( \frac{1}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}-\frac{1}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \right) \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \mu \,\! }[/math] is the loglogistic shape parameter (unknown a priori, the first of two parameters to be found)
- [math]\displaystyle{ \sigma \,\! }[/math] is the loglogistic scale parameter (unknown a priori, the second of two parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval failure data groups,
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
For the purposes of MLE, left censored data will be considered to be intervals with [math]\displaystyle{ T_{Li}^{\prime \prime }=0.\,\! }[/math]
The solution of the maximum log-likelihood function is found by solving for ([math]\displaystyle{ \widehat{\mu },\widehat{\sigma })\,\! }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial \sigma }=0.\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \mu }= & -\frac{\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\mathop{}_{}^{}}}\,}}\,{{N}_{i}}}{\sigma }+\frac{2}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{{{e}^{\tfrac{\ln ({{T}_{i}})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln ({{T}_{i}})-\mu }{\sigma }}}} \\ & +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}}-\frac{{{F}_{I}}}{\sigma } \\ & +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}+\frac{{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \right) \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \sigma }= & -\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{\ln ({{T}_{i}})-\mu }{{{\sigma }^{2}}}-\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\frac{2}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{\tfrac{\ln ({{T}_{i}})-\mu }{\sigma }{{e}^{\tfrac{\ln ({{T}_{i}})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln ({{T}_{i}})-\mu }{\sigma }}}} \\ & +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{i}^{^{\prime }})-\mu }{\sigma }}}} \\ & \frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}(\frac{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}+\frac{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{1+{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}} \\ & -\frac{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}-\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}{{{e}^{\tfrac{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}-{{e}^{\tfrac{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }{\sigma }}}}) \end{align}\,\! }[/math]
The Gumbel Log-Likelihood Functions and their Partials
This log-likelihood function is composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln \left( \frac{{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }-{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}}}}{\sigma } \right) \\ & -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}}} \right) \\ & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}} \right) \end{align}\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} \Lambda = & \underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\left( \frac{{{T}_{i}}-\mu }{\sigma }-{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}} \right)-\ln (\sigma )\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}} \\ & +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}} \\ & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}} \right) \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \mu \,\! }[/math] is the Gumbel shape parameter (unknown a priori, the first of two parameters to be found)
- [math]\displaystyle{ \sigma \,\! }[/math] is the Gumbel scale parameter (unknown a priori, the second of two parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval failure data groups
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
For the purposes of MLE, left censored data will be considered to be intervals with [math]\displaystyle{ T_{Li}^{\prime \prime }=0.\,\! }[/math]
The solution of the maximum log-likelihood function is found by solving for ([math]\displaystyle{ \widehat{\mu },\widehat{\sigma })\,\! }[/math] so that:
- [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial \sigma }=0.\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \mu }= & -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}}-\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}} \\ & +\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}}{{{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}} \right) \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \sigma }= & -\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{{{T}_{i}}-\mu }{{{\sigma }^{2}}}-\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\frac{{{T}_{i}}-\mu }{\sigma }{{e}^{\tfrac{{{T}_{i}}-\mu }{\sigma }}} \\ & -\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{T_{i}^{^{\prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{i}^{^{\prime }}-\mu }{\sigma }}}+\frac{1}{\sigma }\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }} \\ & \left( \frac{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}}{{{e}^{-{{e}^{\tfrac{T_{{{L}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}-{{e}^{-{{e}^{\tfrac{T_{{{R}_{i}}}^{^{\prime \prime }}-\mu }{\sigma }}}}}} \right) \end{align}\,\! }[/math]
The Gamma Log-Likelihood Functions and their Partials
This log-likelihood function is composed of three summation portions:
- [math]\displaystyle{ \begin{align} \ln (L)= & \Lambda =\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln \left( \frac{{{e}^{k(\ln ({{T}_{i}})-\mu )-{{e}^{{{e}^{\ln ({{T}_{i}})-\mu }}}}}}}{{{T}_{i}}\Gamma (k)} \right) \\ & +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( 1-\Gamma \left( _{1}k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu )}} \right) \right) \\ & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right) \right) \end{align}\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} \Lambda = & \underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln ({{T}_{i}})\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln (\Gamma (k))+k\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}(\ln ({{T}_{i}})-\mu ) \\ & \underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{-\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{e}^{\ln ({{T}_{i}})-\mu }} \\ & +\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\ln \left( 1-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }} \right) \right) \\ & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\ln \left( {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu )}} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu )}} \right) \right) \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{F}_{e}}\,\! }[/math] is the number of groups of times-to-failure data points
- [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] time-to-failure data group
- [math]\displaystyle{ \mu \,\! }[/math] is the gamma shape parameter (unknown a priori, the first of two parameters to be found)
- [math]\displaystyle{ k\,\! }[/math] is the gamma scale parameter (unknown a priori, the second of two parameters to be found)
- [math]\displaystyle{ {{T}_{i}}\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of time-to-failure data
- [math]\displaystyle{ S\,\! }[/math] is the number of groups of suspension data points
- [math]\displaystyle{ N_{i}^{\prime }\,\! }[/math] is the number of suspensions in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of suspension data points
- [math]\displaystyle{ T_{i}^{\prime }\,\! }[/math] is the time of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] suspension data group
- [math]\displaystyle{ FI\,\! }[/math] is the number of interval failure data groups
- [math]\displaystyle{ N_{i}^{\prime \prime }\,\! }[/math] is the number of intervals in [math]\displaystyle{ {{i}^{th}}\,\! }[/math] group of data intervals
- [math]\displaystyle{ T_{Li}^{\prime \prime }\,\! }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
- and [math]\displaystyle{ T_{Ri}^{\prime \prime }\,\! }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] interval
For the purposes of MLE, left censored data will be considered to be intervals with [math]\displaystyle{ T_{Li}^{\prime \prime }=0.\,\! }[/math]
The solution of the maximum log-likelihood function is found by solving for ([math]\displaystyle{ \widehat{\mu },\widehat{\sigma })\,\! }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial \mu }=0,\tfrac{\partial \Lambda }{\partial k}=0.\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \mu }= & -k\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}+\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{e}^{\ln ({{T}_{i}})-\mu }} \\ & +\frac{1}{\Gamma (k)}\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{{{e}^{k\left( \ln (T_{i}^{^{\prime }})-\mu )-{{e}^{\ln (T_{i}^{^{\prime }})-\mu )}} \right)}}}{1-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }} \right)} \\ & +\frac{1}{\Gamma (k)}\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\{\frac{{{e}^{k{{e}^{{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }}}}-{{e}^{{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }}}}}}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)} \\ & -\frac{{{e}^{k{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}-{{e}^{{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}}}}}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)}\} \end{align}\,\! }[/math]
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial k}= & \underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}(\ln ({{T}_{i}})-\mu )-\frac{{{\Gamma }^{^{\prime }}}(k)\underset{i=1}{\mathop{\overset{{{F}_{e}}}{\mathop{\mathop{}_{}^{}}}\,}}\,{{N}_{i}}}{\Gamma (k)} \\ & -\underset{i=1}{\mathop{\overset{S}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime }}\frac{\tfrac{\partial {{\Gamma }_{1}}(k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }})}{\partial k}}{1-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{i}^{^{\prime }})-\mu }} \right)} \\ & +\underset{i=1}{\mathop{\overset{{{F}_{I}}}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{^{\prime \prime }}\left( \frac{\tfrac{\partial {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }} \right)}{\partial k}-\tfrac{\partial {{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)}{\partial k}}{{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{R}_{i}}}^{^{\prime \prime }})-\mu }} \right)-{{\Gamma }_{1}}\left( k;{{e}^{\ln (T_{{{L}_{i}}}^{^{\prime \prime }})-\mu }}) \right)} \right) \end{align}\,\! }[/math]