Warranty Data Analysis: Difference between revisions
| (11 intermediate revisions by 4 users not shown) | |||
| Line 10: | Line 10: | ||
==Nevada Chart Format== | ==Nevada Chart Format== | ||
The Nevada format allows the user to convert shipping and warranty return data into the standard reliability data form of failures and suspensions so that it can easily be analyzed with traditional life data analysis methods. For each time period in which a number of products are shipped, there will be a certain number of returns or failures in subsequent time periods, while the rest of the population that was shipped will continue to operate in the following time periods. For example, if 500 units are shipped in May, and 10 of those units are warranty returns in June, that is equivalent to 10 failures at a time of one month. The other | The Nevada format allows the user to convert shipping and warranty return data into the standard reliability data form of failures and suspensions so that it can easily be analyzed with traditional life data analysis methods. For each time period in which a number of products are shipped, there will be a certain number of returns or failures in subsequent time periods, while the rest of the population that was shipped will continue to operate in the following time periods. For example, if 500 units are shipped in May, and 10 of those units are warranty returns in June, that is equivalent to 10 failures at a time of one month. The other 490 units will go on to operate and possibly fail in the months that follow. This information can be arranged in a diagonal chart, as shown in the following figure. | ||
[[Image:Nevada-Chart-Illustration.png|center|450px| ]] | [[Image:Nevada-Chart-Illustration.png|center|450px| ]] | ||
| Line 20: | Line 20: | ||
A company keeps track of its shipments and warranty returns on a month-by-month basis. The following table records the shipments in June, July and August, and the warranty returns through September: | A company keeps track of its shipments and warranty returns on a month-by-month basis. The following table records the shipments in June, July and August, and the warranty returns through September: | ||
{|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | {|border="1" align="center" style="border-collapse: collapse;" cellpadding="5" cellspacing="5" | ||
| Line 34: | Line 35: | ||
|} | |} | ||
We will examine the data month by month. In June 100 units were sold, and in July 3 of these units were returned. This gives 3 failures at one month for the June shipment, which we will denote as <math>{{F}_{JUN,1}}=3\,\!</math> . Likewise, 3 failures occurred in August and 5 occurred in September for this shipment, or | |||
We will examine the data month by month. In June 100 units were sold, and in July 3 of these units were returned. This gives 3 failures at one month for the June shipment, which we will denote as <math>{{F}_{JUN,1}}=3\,\!</math>. Likewise, 3 failures occurred in August and 5 occurred in September for this shipment, or <math>{{F}_{JUN,2}}=3\,\!</math> and <math>{{F}_{JUN,3}}=5\,\!</math>. Consequently, at the end of our three-month analysis period, there were a total of 11 failures for the 100 units shipped in June. This means that 89 units are presumably still operating, and can be considered suspensions at three months, or <math>{{S}_{JUN,3}}=89\,\!</math>. For the shipment of 140 in July, 2 were returned the following month, or <math>{{F}_{JUL,1}}=2\,\!</math>, and 4 more were returned the month after that, or <math>{{F}_{JUL,2}}=4\,\!</math>. After two months, there are 134 ( <math>140-2-4=134\,\!</math> ) units from the July shipment still operating, or <math>{{S}_{JUL,2}}=134\,\!</math>. For the final shipment of 150 in August, 4 fail in September, or <math>{{F}_{AUG,1}}=4\,\!</math>, with the remaining 146 units being suspensions at one month, or <math>{{S}_{AUG,1}}=146\,\!</math>. | |||
It is now a simple matter to add up the number of failures for 1, 2, and 3 months, then add the suspensions to get our reliability data set: | It is now a simple matter to add up the number of failures for 1, 2, and 3 months, then add the suspensions to get our reliability data set: | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 45: | Line 48: | ||
\text{Failures at 3 months:} & {{F}_{3}}={{F}_{JUN,3}}=5 \\ | \text{Failures at 3 months:} & {{F}_{3}}={{F}_{JUN,3}}=5 \\ | ||
\text{Suspensions at 3 months:} & {{S}_{JUN,3}}=89 \\ | \text{Suspensions at 3 months:} & {{S}_{JUN,3}}=89 \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
These calculations can be performed automatically in Weibull++. | |||
<div class="noprint"> | |||
{{Examples Box|Weibull++_Examples|<p>More Nevada chart format warranty analysis examples are available! See also:</p> | |||
{{Examples Both|http://www.reliasoft.com/Weibull/examples/rc5/index.htm|Warranty Analysis Example|http://www.reliasoft.tv/weibull/appexamples/weibull_app_ex_5.html|Watch the video...}}<nowiki/> | |||
}} | |||
</div> | |||
==Time-to-Failure Format== | ==Time-to-Failure Format== | ||
| Line 70: | Line 80: | ||
Alternatively, and more realistically, instead of using an average usage, an actual distribution that reflects the variation in usage and customer behavior can be used. This distribution describes the usage of a unit over a certain time period (e.g., 1 year, 1 month, etc). This probabilistic model can be used to estimate the usage for all surviving components in service and the percentage of users running the product at different usage rates. In the automotive example, for instance, such a distribution can be used to calculate the percentage of customers that drive 0-200 miles/month, 200-400 miles/month, etc. We can take these percentages and multiply them by the number of suspensions to find the number of items that have been accumulating usage values in these ranges. | Alternatively, and more realistically, instead of using an average usage, an actual distribution that reflects the variation in usage and customer behavior can be used. This distribution describes the usage of a unit over a certain time period (e.g., 1 year, 1 month, etc). This probabilistic model can be used to estimate the usage for all surviving components in service and the percentage of users running the product at different usage rates. In the automotive example, for instance, such a distribution can be used to calculate the percentage of customers that drive 0-200 miles/month, 200-400 miles/month, etc. We can take these percentages and multiply them by the number of suspensions to find the number of items that have been accumulating usage values in these ranges. | ||
To proceed with applying a usage distribution, the usage distribution is divided into increments based on a specified interval width denoted as | To proceed with applying a usage distribution, the usage distribution is divided into increments based on a specified interval width denoted as <math>Z\,\!</math>. The usage distribution, <math>Q\,\!</math>, is divided into intervals of <math>0+Z\,\!</math>, <math>Z+Z\,\!</math>, <math>2Z+Z\,\!</math>, etc., or <math>{{x}_{i}}={{x}_{i-1}}+Z\,\!</math>, as shown in the next figure. | ||
[[Image:Usage pdf Plot.png|center|250px| ]] | [[Image:Usage pdf Plot.png|center|250px| ]] | ||
| Line 78: | Line 88: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
F({{x}_{i}})=Q({{x}_{i}})-Q({{x}_{i}}-1) | F({{x}_{i}})=Q({{x}_{i}})-Q({{x}_{i}}-1) | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
::<math>Q()</math> | ::<math>Q()\,\!</math> is the usage distribution Cumulative Density Function, ''cdf''. | ||
::<math>x</math> | ::<math>x\,\!</math> represents the intervals used in apportioning the suspended population. | ||
A suspension group is a collection of suspensions that have the same age. The percentage of suspensions can be translated to numbers of suspensions within each interval, | A suspension group is a collection of suspensions that have the same age. The percentage of suspensions can be translated to numbers of suspensions within each interval, <math>{{x}_{i}}\,\!</math>. This is done by taking each group of suspensions and multiplying it by each <math>F({{x}_{i}})\,\!</math>, or: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
| Line 93: | Line 103: | ||
& & ... \\ | & & ... \\ | ||
& {{N}_{n,j}}= & F({{x}_{n}})\times N{{S}_{j}} | & {{N}_{n,j}}= & F({{x}_{n}})\times N{{S}_{j}} | ||
\end{align}</math> | \end{align}\,\!</math> | ||
where: | where: | ||
::<math>{{N}_{n,j}}</math> | ::<math>{{N}_{n,j}}\,\!</math> is the number of suspensions that belong to each interval. | ||
::<math>N{{S}_{j}}</math> | ::<math>N{{S}_{j}}\,\!</math> is the jth group of suspensions from the data set. | ||
This is repeated for all the groups of suspensions. | This is repeated for all the groups of suspensions. | ||
The age of the suspensions is calculated by subtracting the Date In-Service ( <math>DIS</math> ), which is the date at which the unit started operation, from the end of observation period date or End Date ( <math>ED</math> ). This is the Time In-Service ( <math>TIS</math> ) value that describes the age of the surviving unit. | The age of the suspensions is calculated by subtracting the Date In-Service ( <math>DIS\,\!</math> ), which is the date at which the unit started operation, from the end of observation period date or End Date ( <math>ED\,\!</math> ). This is the Time In-Service ( <math>TIS\,\!</math> ) value that describes the age of the surviving unit. | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
TIS=ED-DIS | TIS=ED-DIS | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Note: | Note: <math>TIS\,\!</math> is in the same time units as the period in which the usage distribution is defined. | ||
For each | For each <math>{{N}_{k,j}}\,\!</math>, the usage is calculated as: | ||
::<math>Uk,j=xi\times TISj</math> | ::<math>Uk,j=xi\times TISj\,\!</math> | ||
After this step, the usage of each suspension group is estimated. This data can be combined with the failures data set, and a failure distribution can be fitted to the combined data. | After this step, the usage of each suspension group is estimated. This data can be combined with the failures data set, and a failure distribution can be fitted to the combined data. | ||
| Line 150: | Line 160: | ||
Use the Weibull parameter estimates to determine the conditional probability of failure for each shipment time period, and then multiply that probability with the number of units that are at risk for that period as follows. The equation for the conditional probability of failure is given by: | Use the Weibull parameter estimates to determine the conditional probability of failure for each shipment time period, and then multiply that probability with the number of units that are at risk for that period as follows. The equation for the conditional probability of failure is given by: | ||
::<math>Q(t|T)=1-R(t|T)=1-\frac{R(T+t)}{R(T)}</math> | ::<math>Q(t|T)=1-R(t|T)=1-\frac{R(T+t)}{R(T)}\,\!</math> | ||
For the June shipment, there are 89 units that have successfully operated until the end of September ( <math>T=3 | For the June shipment, there are 89 units that have successfully operated until the end of September ( <math>T=3 months)\,\!</math>. The probability of one of these units failing in the next month ( <math>t=1 month)\,\!</math> is then given by: | ||
::<math>Q(1|3)=1-\frac{R(4)}{R(3)}=1-\frac{{{e}^{-{{\left( \tfrac{4}{6.70} \right)}^{2.49}}}}}{{{e}^{-{{\left( \tfrac{3}{6.70} \right)}^{2.49}}}}}=1-\frac{0.7582}{0.8735}=0.132</math> | ::<math>Q(1|3)=1-\frac{R(4)}{R(3)}=1-\frac{{{e}^{-{{\left( \tfrac{4}{6.70} \right)}^{2.49}}}}}{{{e}^{-{{\left( \tfrac{3}{6.70} \right)}^{2.49}}}}}=1-\frac{0.7582}{0.8735}=0.132\,\!</math> | ||
Once the probability of failure for an additional month of operation is determined, the expected number of failed units during the next month, from the June shipment, is the product of this probability and the number of units at risk ( <math>{{S}_{JUN,3}}=89)</math> | Once the probability of failure for an additional month of operation is determined, the expected number of failed units during the next month, from the June shipment, is the product of this probability and the number of units at risk ( <math>{{S}_{JUN,3}}=89)\,\!</math> or: | ||
::<math>{{\widehat{F}}_{JUN,4}}=89\cdot 0.132=11.748\text{, or 12 units}</math> | ::<math>{{\widehat{F}}_{JUN,4}}=89\cdot 0.132=11.748\text{, or 12 units}\,\!</math> | ||
This is then repeated for the July shipment, where there were 134 units operating at the end of September, with an exposure time of two months. The probability of failure in the next month is: | This is then repeated for the July shipment, where there were 134 units operating at the end of September, with an exposure time of two months. The probability of failure in the next month is: | ||
::<math>Q(1|2)=1-\frac{R(3)}{R(2)}=1-\frac{0.8735}{0.9519}=0.0824</math> | ::<math>Q(1|2)=1-\frac{R(3)}{R(2)}=1-\frac{0.8735}{0.9519}=0.0824\,\!</math> | ||
This value is multiplied by | This value is multiplied by <math>{{S}_{JUL,2}}=134\,\!</math> to determine the number of failures, or: | ||
::<math>{{\widehat{F}}_{JUL,3}}=134\cdot 0.0824=11.035\text{, or 11 units}</math> | ::<math>{{\widehat{F}}_{JUL,3}}=134\cdot 0.0824=11.035\text{, or 11 units}\,\!</math> | ||
For the August shipment, there were 146 units operating at the end of September, with an exposure time of one month. The probability of failure in the next month is: | For the August shipment, there were 146 units operating at the end of September, with an exposure time of one month. The probability of failure in the next month is: | ||
::<math>Q(1|1)=1-\frac{R(2)}{R(1)}=1-\frac{0.9519}{0.9913}=0.0397</math> | ::<math>Q(1|1)=1-\frac{R(2)}{R(1)}=1-\frac{0.9519}{0.9913}=0.0397\,\!</math> | ||
This value is multiplied by | This value is multiplied by <math>{{S}_{AUG,1}}=146\,\!</math> to determine the number of failures, or: | ||
::<math>{{\widehat{F}}_{AUG,2}}=146\cdot 0.0397=5.796\text{, or 6 units}</math> | ::<math>{{\widehat{F}}_{AUG,2}}=146\cdot 0.0397=5.796\text{, or 6 units}\,\!</math> | ||
Thus, the total expected returns from all shipments for the next month is the sum of the above, or 29 units. This method can be easily repeated for different future sales periods, and utilizing projected shipments. If the user lists the number of units that are expected be sold or shipped during future periods, then these units are added to the number of units at risk whenever they are introduced into the field. The '''Generate Forecast''' functionality in the Weibull++ warranty analysis folio can automate this process for you. | Thus, the total expected returns from all shipments for the next month is the sum of the above, or 29 units. This method can be easily repeated for different future sales periods, and utilizing projected shipments. If the user lists the number of units that are expected be sold or shipped during future periods, then these units are added to the number of units at risk whenever they are introduced into the field. The '''Generate Forecast''' functionality in the Weibull++ warranty analysis folio can automate this process for you. | ||
| Line 194: | Line 204: | ||
===Basic Analysis Method=== | ===Basic Analysis Method=== | ||
For each sales period | For each sales period <math>i\,\!</math> and return period <math>j\,\!</math>, the prediction error can be calculated as follows: | ||
::<math>{{e}_{i,j}}={{\hat{F}}_{i,j}}-{{F}_{i,j}}</math> | ::<math>{{e}_{i,j}}={{\hat{F}}_{i,j}}-{{F}_{i,j}}\,\!</math> | ||
where | where <math>{{\hat{F}}_{i,j}}\,\!</math> is the estimated number of failures based on the estimated distribution parameters for the sales period <math>i\,\!</math> and the return period <math>j\,\!</math>, which is calculated using the equation for the conditional probability, and <math>{{F}_{i,j}}\,\!</math> is the actual number of failure for the sales period <math>i\,\!</math> and the return period <math>j\,\!</math>. | ||
Since we are assuming that the model is accurate, | Since we are assuming that the model is accurate, <math>{{e}_{i,j}}\,\!</math> should follow a normal distribution with mean value of zero and a standard deviation <math>s\,\!</math>, where: | ||
::<math>{{\bar{e}}_{i,j}}=\frac{\underset{i}{\mathop{\sum }}\,\underset{j}{\mathop{\sum }}\,{{e}_{i,j}}}{n}=0</math> | ::<math>{{\bar{e}}_{i,j}}=\frac{\underset{i}{\mathop{\sum }}\,\underset{j}{\mathop{\sum }}\,{{e}_{i,j}}}{n}=0\,\!</math> | ||
and | and <math>n\,\!</math> is the total number of return data (total number of residuals). | ||
The estimated standard deviation of the prediction errors can then be calculated by: | The estimated standard deviation of the prediction errors can then be calculated by: | ||
::<math>s=\sqrt{\frac{1}{n-1}\underset{i}{\mathop \sum }\,\underset{j}{\mathop \sum }\,e_{i,j}^{2}}</math> | ::<math>s=\sqrt{\frac{1}{n-1}\underset{i}{\mathop \sum }\,\underset{j}{\mathop \sum }\,e_{i,j}^{2}}\,\!</math> | ||
and | and <math>{{e}_{i,j}}\,\!</math> can be normalized as follows: | ||
::<math>{{z}_{i,j}}=\frac{{{e}_{i,j}}}{s}</math> | ::<math>{{z}_{i,j}}=\frac{{{e}_{i,j}}}{s}\,\!</math> | ||
where | where <math>{{z}_{i,j}}\,\!</math> is the standardized error. <math>{{z}_{i,j}}\,\!</math> follows a normal distribution with <math>\mu =0\,\!</math> and <math>\sigma =1\,\!</math>. | ||
It is known that the square of a random variable with standard normal distribution follows the | It is known that the square of a random variable with standard normal distribution follows the <math>{{\chi }^{2}}\,\!</math> (Chi Square) distribution with 1 degree of freedom and that the sum of the squares of <math>m\,\!</math> random variables with standard normal distribution follows the <math>{{\chi }^{2}}\,\!</math> distribution with <math>m\,\!</math> degrees of freedom. This then can be used to help detect the abnormal returns for a given sales period, return period or just a specific cell (combination of a return and a sales period). | ||
:* For a cell, abnormality is detected if | :* For a cell, abnormality is detected if <math>z_{i,j}^{2}=\chi _{1}^{2}\ge \chi _{1,\alpha }^{2}.\,\!</math> | ||
:* For an entire sales period | :* For an entire sales period <math>i\,\!</math>, abnormality is detected if <math>\underset{j}{\mathop{\sum }}\,z_{i,j}^{2}=\chi _{J}^{2}\ge \chi _{\alpha ,J}^{2},\,\!</math> where <math>J\,\!</math> is the total number of return period for a sales period <math>i\,\!</math>. | ||
:* For an entire return period | :* For an entire return period <math>j\,\!</math>, abnormality is detected if <math>\underset{i}{\mathop{\sum }}\,z_{i,j}^{2}=\chi _{I}^{2}\ge \chi _{\alpha ,I}^{2},\,\!</math> where <math>I\,\!</math> is the total number of sales period for a return period <math>j\,\!</math>. | ||
Here | Here <math>\alpha \,\!</math> is the criticality value of the <math>{{\chi }^{2}}\,\!</math> distribution, which can be set at critical value or caution value. It describes the level of sensitivity to outliers (returns that deviate significantly from the predictions based on the fitted model). Increasing the value of <math>\alpha \,\!</math> increases the power of detection, but this could lead to more false alarms. | ||
====Example==== | ====Example==== | ||
| Line 241: | Line 251: | ||
|} | |} | ||
For example, for the month of September, the expected return number is given by: | For example, for the month of September, the expected return number from the June shipment is given by: | ||
::<math>{{\hat{F}}_{Jun,3}}=(100-6)\cdot \left( 1-\frac{R(3)}{R(2)} \right)=94\cdot 0.08239=7.7447</math> | ::<math>{{\hat{F}}_{Jun,3}}=(100-6)\cdot \left( 1-\frac{R(3)}{R(2)} \right)=94\cdot 0.08239=7.7447\,\!</math> | ||
The actual number of returns during this period is five; thus, the prediction error for this period is: | The actual number of returns during this period is five; thus, the prediction error for this period is: | ||
::<math>{{e}_{Jun,3}}={{\hat{F}}_{Jun,3}}-{{F}_{Jun,3}}=7.7447-5=2.7447.</math> | ::<math>{{e}_{Jun,3}}={{\hat{F}}_{Jun,3}}-{{F}_{Jun,3}}=7.7447-5=2.7447.\,\!</math> | ||
This can then be repeated for each cell, yielding the following table for | This can then be repeated for each cell, yielding the following table for <math>{{e}_{i,j}}\,\!</math> : | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 257: | Line 267: | ||
\text{Jul}\text{. 2005} & \text{140} & \text{-} & \text{-0}\text{.7816} & \text{1}\text{.4719} \\ | \text{Jul}\text{. 2005} & \text{140} & \text{-} & \text{-0}\text{.7816} & \text{1}\text{.4719} \\ | ||
\text{Aug}\text{. 2005} & \text{150} & \text{-} & \text{-} & \text{-2}\text{.6946} \\ | \text{Aug}\text{. 2005} & \text{150} & \text{-} & \text{-} & \text{-2}\text{.6946} \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
Now, for this example, | Now, for this example, <math>n=6\,\!</math>, <math>{{\bar{e}}_{i,j}}=-0.0904\,\!</math> and <math>s=2.1366.\,\!</math> | ||
Thus the <math>z_{i,j}</math> values are: | Thus the <math>z_{i,j}\,\!</math> values are: | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 269: | Line 279: | ||
\text{Jul}\text{. 2005} & \text{140} & \text{-} & \text{-0}\text{.3658} & \text{0}\text{.6889} \\ | \text{Jul}\text{. 2005} & \text{140} & \text{-} & \text{-0}\text{.3658} & \text{0}\text{.6889} \\ | ||
\text{Aug}\text{. 2005} & \text{150} & \text{-} & \text{-} & \text{-1}\text{.2612} \\ | \text{Aug}\text{. 2005} & \text{150} & \text{-} & \text{-} & \text{-1}\text{.2612} \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
The | The <math>z_{i,j}^{2}\,\!</math> values, for each cell, are given in the following table. | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 280: | Line 290: | ||
\text{Aug}\text{. 2005} & \text{150} & \text{-} & \text{-} & \text{1}\text{.5905} & 1.5905 \\ | \text{Aug}\text{. 2005} & \text{150} & \text{-} & \text{-} & \text{1}\text{.5905} & 1.5905 \\ | ||
\text{Sum} & {} & 0.9936 & 0.2907 & 3.7157 & {} \\ | \text{Sum} & {} & 0.9936 & 0.2907 & 3.7157 & {} \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
If the critical value is set at | If the critical value is set at <math>\alpha = 0.01\,\!</math> and the caution value is set at <math>\alpha = 0.1\,\!</math>, then the critical and caution <math>{{\chi }^{2}}\,\!</math> values will be: | ||
<center><math>\begin{matrix} | <center><math>\begin{matrix} | ||
| Line 289: | Line 299: | ||
{{\chi}^{2}\text{Critical}} & \text{6.6349} & \text{9.2103} & \text{11.3449} \\ | {{\chi}^{2}\text{Critical}} & \text{6.6349} & \text{9.2103} & \text{11.3449} \\ | ||
{{\chi}^{2}\text{Caution}} & \text{2,7055} & \text{4.6052} & \text{6.2514} \\ | {{\chi}^{2}\text{Caution}} & \text{2,7055} & \text{4.6052} & \text{6.2514} \\ | ||
\end{matrix}</math></center> | \end{matrix}\,\!</math></center> | ||
If we consider the sales periods as the basis for outlier detection, then after comparing the above table to the sum of | If we consider the sales periods as the basis for outlier detection, then after comparing the above table to the sum of <math>z_{i,j}^{2}\,\!</math> <math>(\chi _{1}^{2})\,\!</math> values for each sales period, we find that all the sales values do not exceed the critical and caution limits. For example, the total <math>{{\chi }^{2}}\,\!</math> value of the sale month of July is 0.6085. Its degrees of freedom is 2, so the corresponding caution and critical values are 4.6052 and 9.2103 respectively. Both values are larger than 0.6085, so the return numbers of the July sales period do not deviate (based on the chosen significance) from the model's predictions. | ||
If we consider returns periods as the basis for outliers detection, then after comparing the above table to the sum of | If we consider returns periods as the basis for outliers detection, then after comparing the above table to the sum of <math>z_{i,j}^{2}\,\!</math> <math>(\chi _{1}^{2})\,\!</math> values for each return period, we find that all the return values do not exceed the critical and caution limits. For example, the total <math>{{\chi }^{2}}\,\!</math> value of the sale month of August is 3.7157. Its degree of freedom is 3, so the corresponding caution and critical values are 6.2514 and 11.3449 respectively. Both values are larger than 3.7157, so the return numbers for the June return period do not deviate from the model's predictions. | ||
This analysis can be automatically performed in Weibull++ by entering the alpha values in the Statistical Process Control page of the control panel and selecting which period to color code, as shown next. | This analysis can be automatically performed in Weibull++ by entering the alpha values in the Statistical Process Control page of the control panel and selecting which period to color code, as shown next. | ||
| Line 299: | Line 309: | ||
[[Image:Warranty Example 5 SPC settings.png|center|250px| ]] | [[Image:Warranty Example 5 SPC settings.png|center|250px| ]] | ||
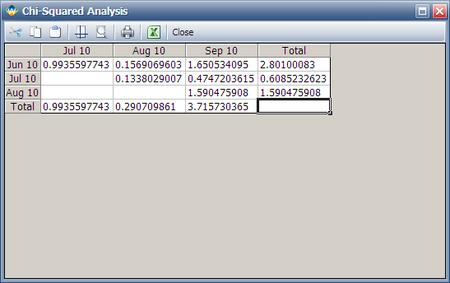
To view the table of chi-squared values ( | To view the table of chi-squared values ( <math>z_{i,j}^{2}\,\!</math> or <math>\chi _{1}^{2}\,\!</math> values), click the '''Show Results (...)''' button. | ||
[[Image:Warranty Example 5 Chi-square.png|center|450px| ]] | [[Image:Warranty Example 5 Chi-square.png|center|450px| ]] | ||
Latest revision as of 15:37, 16 August 2017
The Weibull++ warranty analysis folio provides four different data entry formats for warranty claims data. It allows the user to automatically perform life data analysis, predict future failures (through the use of conditional probability analysis), and provides a method for detecting outliers. The four data-entry formats for storing sales and returns information are:
- 1) Nevada Chart Format
- 2) Time-to-Failure Format
- 3) Dates of Failure Format
- 4) Usage Format
These formats are explained in the next sections. We will also discuss some specific warranty analysis calculations, including warranty predictions, analysis of non-homogeneous warranty data and using statistical process control (SPC) to monitor warranty returns.
Nevada Chart Format
The Nevada format allows the user to convert shipping and warranty return data into the standard reliability data form of failures and suspensions so that it can easily be analyzed with traditional life data analysis methods. For each time period in which a number of products are shipped, there will be a certain number of returns or failures in subsequent time periods, while the rest of the population that was shipped will continue to operate in the following time periods. For example, if 500 units are shipped in May, and 10 of those units are warranty returns in June, that is equivalent to 10 failures at a time of one month. The other 490 units will go on to operate and possibly fail in the months that follow. This information can be arranged in a diagonal chart, as shown in the following figure.
At the end of the analysis period, all of the units that were shipped and have not failed in the time since shipment are considered to be suspensions. This process is repeated for each shipment and the results tabulated for each particular failure and suspension time prior to reliability analysis. This process may sound confusing, but it is actually just a matter of careful bookkeeping. The following example illustrates this process.
Example
Nevada Chart Format Calculations Example
A company keeps track of its shipments and warranty returns on a month-by-month basis. The following table records the shipments in June, July and August, and the warranty returns through September:
| RETURNS | ||||
| SHIP | Jul. 2010 | Aug. 2010 | Sep. 2010 | |
| Jun. 2010 | 100 | 3 | 3 | 5 |
| Jul. 2010 | 140 | - | 2 | 4 |
| Aug. 2010 | 150 | - | - | 4 |
We will examine the data month by month. In June 100 units were sold, and in July 3 of these units were returned. This gives 3 failures at one month for the June shipment, which we will denote as [math]\displaystyle{ {{F}_{JUN,1}}=3\,\! }[/math]. Likewise, 3 failures occurred in August and 5 occurred in September for this shipment, or [math]\displaystyle{ {{F}_{JUN,2}}=3\,\! }[/math] and [math]\displaystyle{ {{F}_{JUN,3}}=5\,\! }[/math]. Consequently, at the end of our three-month analysis period, there were a total of 11 failures for the 100 units shipped in June. This means that 89 units are presumably still operating, and can be considered suspensions at three months, or [math]\displaystyle{ {{S}_{JUN,3}}=89\,\! }[/math]. For the shipment of 140 in July, 2 were returned the following month, or [math]\displaystyle{ {{F}_{JUL,1}}=2\,\! }[/math], and 4 more were returned the month after that, or [math]\displaystyle{ {{F}_{JUL,2}}=4\,\! }[/math]. After two months, there are 134 ( [math]\displaystyle{ 140-2-4=134\,\! }[/math] ) units from the July shipment still operating, or [math]\displaystyle{ {{S}_{JUL,2}}=134\,\! }[/math]. For the final shipment of 150 in August, 4 fail in September, or [math]\displaystyle{ {{F}_{AUG,1}}=4\,\! }[/math], with the remaining 146 units being suspensions at one month, or [math]\displaystyle{ {{S}_{AUG,1}}=146\,\! }[/math].
It is now a simple matter to add up the number of failures for 1, 2, and 3 months, then add the suspensions to get our reliability data set:
These calculations can be performed automatically in Weibull++.
Time-to-Failure Format
This format is similar to the standard folio data entry format (all number of units, failure times and suspension times are entered by the user). The difference is that when the data is used within the context of warranty analysis, the ability to generate forecasts is available to the user.
Example
Times-to-Failure Format Warranty Analysis
Assume that we have the following information for a given product.
| Number in State | State F or S | State End Time (Hr) |
| 2 | F | 100 |
| 3 | F | 125 |
| 5 | F | 175 |
| 1500 | S | 200 |
| Quantity In-Service | Time (Hr) |
| 500 | 200 |
| 400 | 300 |
| 100 | 500 |
Use the time-to-failure warranty analysis folio to analyze the data and generate a forecast for future returns.
Solution
Create a warranty analysis folio and select the times-to-failure format. Enter the data from the tables in the Data and Future Sales sheets, and then analyze the data using the 2P-Weibull distribution and RRX analysis method. The parameters are estimated to be beta = 3.199832 and eta=814.293442.
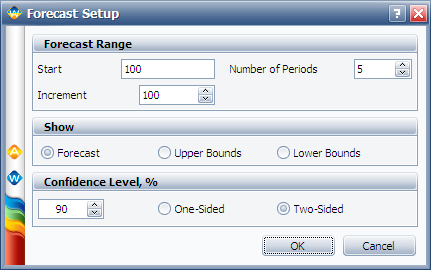
Click the Forecast icon on the control panel. In the Forecast Setup window, set the forecast to start on the 100th hour and set the number of forecast periods to 5. Set the increment (length of each period) to 100, as shown next.
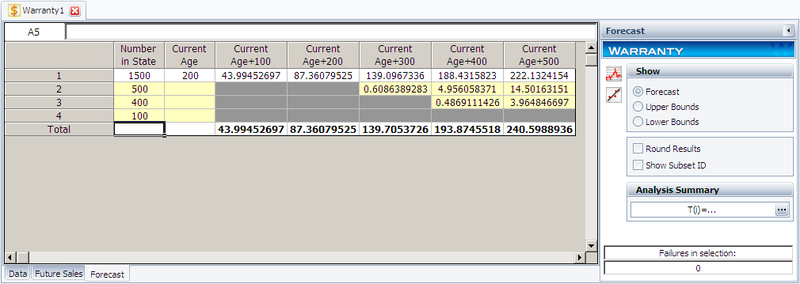
Click OK. A Forecast sheet will be created, with the following predicted future returns.
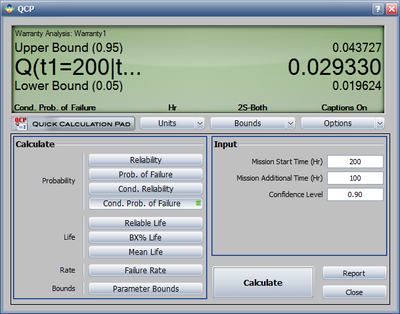
We will use the first row to explain how the forecast for each cell is calculated. For example, there are 1,500 units with a current age of 200 hours. The probability of failure in the next 100 hours can be calculated in the QCP, as follows.
Therefore, the predicted number of failures for the first 100 hours is:
- [math]\displaystyle{ 1500\times 0.02932968=43.99452\,\! }[/math]
This is identical to the result given in the Forecast sheet (shown in the 3rd cell in the first row) of the analysis. The bounds and the values in other cells can be calculated similarly.
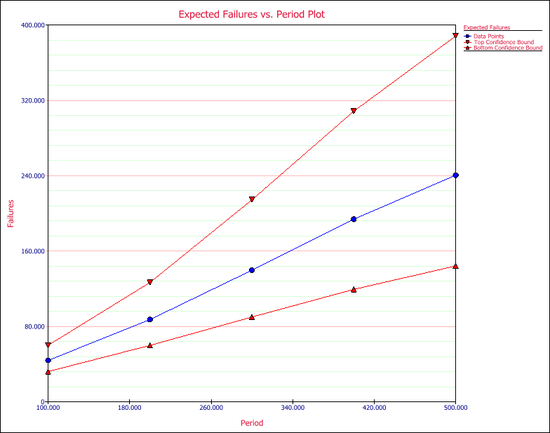
All the plots that are available for the standard folio are also available in the warranty analysis, such as the Probability plot, Reliability plot, etc. One additional plot in warranty analysis is the Expected Failures plot, which shows the expected number of failures over time. The following figure shows the Expected Failures plot of the example, with confidence bounds.
Dates of Failure Format
Another common way for reporting field information is to enter a date and quantity of sales or shipments (Quantity In-Service data) and the date and quantity of returns (Quantity Returned data). In order to identify which lot the unit comes from, a failure is identified by a return date and the date of when it was put in service. The date that the unit went into service is then associated with the lot going into service during that time period. You can use the optional Subset ID column in the data sheet to record any information to identify the lots.
Example
Dates of Failure Warranty Analysis
Assume that a company has the following information for a product.
| Quantity In-Service | Date In-Service |
| 6316 | 1/1/2010 |
| 8447 | 2/1/2010 |
| 5892 | 3/1/2010 |
| 596 | 4/1/2010 |
| 996 | 5/1/2010 |
| 8977 | 6/1/2010 |
| 2578 | 7/1/2010 |
| 8318 | 8/1/2010 |
| 2667 | 9/1/2010 |
| 7452 | 10/1/2010 |
| 1533 | 11/1/2010 |
| 9393 | 12/1/2010 |
| 1966 | 1/1/2011 |
| 8960 | 2/1/2011 |
| 6341 | 3/1/2011 |
| 4005 | 4/1/2011 |
| 3784 | 5/1/2011 |
| 5426 | 6/1/2011 |
| 4958 | 7/1/2011 |
| 6981 | 8/1/2011 |
| Quantity Returned | Date of Return | Date In-Service |
| 2 | 10/29/2010 | 10/1/2010 |
| 1 | 11/13/2010 | 10/1/2010 |
| 2 | 3/15/2011 | 10/1/2010 |
| 5 | 4/10/2011 | 10/1/2010 |
| 1 | 11/13/2010 | 11/1/2010 |
| 2 | 2/19/2011 | 11/1/2010 |
| 1 | 3/11/2011 | 11/1/2010 |
| 2 | 5/18/2011 | 11/1/2010 |
| 1 | 1/9/2011 | 12/1/2010 |
| 2 | 2/13/2011 | 12/1/2010 |
| 1 | 3/2/2011 | 12/1/2010 |
| 1 | 6/7/2011 | 12/1/2010 |
| 1 | 4/28/2011 | 1/1/2011 |
| 2 | 6/15/2011 | 1/1/2011 |
| 3 | 7/15/2011 | 1/1/2011 |
| 1 | 8/10/2011 | 2/1/2011 |
| 1 | 8/12/2011 | 2/1/2011 |
| 1 | 8/14/2011 | 2/1/2011 |
| Quantity In-Service | Date In-Service |
| 5000 | 9/1/2011 |
| 5000 | 10/1/2011 |
| 5000 | 11/1/2011 |
| 5000 | 12/1/2011 |
| 5000 | 1/1/2012 |
Using the given information to estimate the failure distribution of the product and forecast warranty returns.
Solution
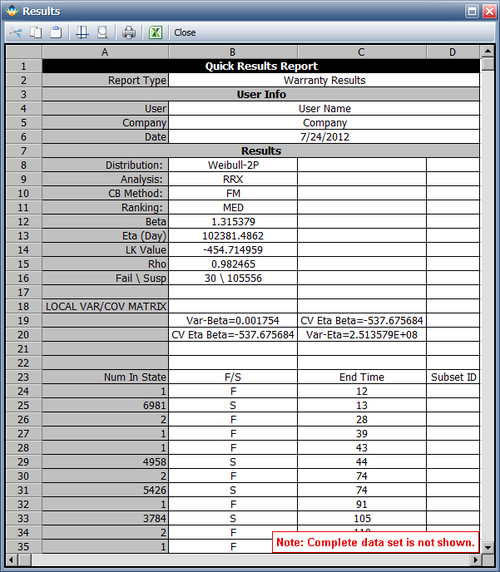
Create a warranty analysis folio using the dates of failure format. Enter the data from the tables in the Sales, Returns and Future Sales sheets. On the control panel, click the Auto-Set button to automatically set the end date to the last day the warranty data were collected (September 14, 2011). Analyze the data using the 2P-Weibull distribution and RRX analysis method. The parameters are estimated to be beta = 1.315379 and eta = 102,381.486165.
The warranty folio automatically converts the warranty data into a format that can be used in a Weibull++ standard folio. To see this result, click anywhere within the Analysis Summary area of the control panel to open a report, as shown next (showing only the first 35 rows of data). In this example, rows 23 to 60 show the time-to-failure data that resulted from the conversion.
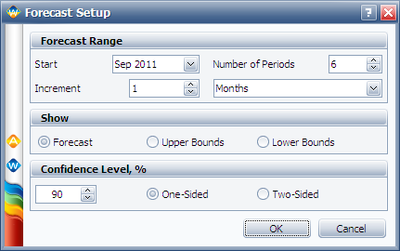
To generate a forecast, click the Forecast icon on the control panel. In the Forecast Setup window, set the forecast to start on September 2011 and set the number of forecast periods to 6. Set the increment (length of each period) to 1 Month, as shown next.
Click OK. A Forecast sheet will be created, with the predicted future returns. Note that the first forecast will start on September 15, 2011 because the end of observation period was set to September 14, 2011.
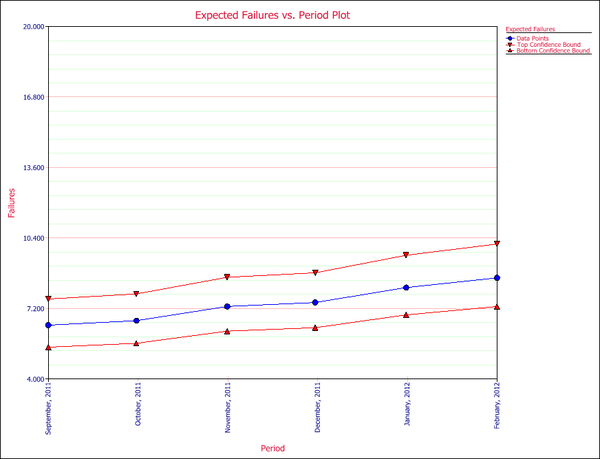
Click the Plot icon and choose the Expected Failures plot. The plot displays the predicted number of returns for each month, as shown next.
Usage Format
Often, the driving factor for reliability is usage rather than time. For example, in the automotive industry, the failure behavior in the majority of the products is mileage-dependent rather than time-dependent. The usage format allows the user to convert shipping and warranty return data into the standard reliability data for of failures and suspensions when the return information is based on usage rather than return dates or periods. Similar to the dates of failure format, a failure is identified by the return number and the date of when it was put in service in order to identify which lot the unit comes from. The date that the returned unit went into service associates the returned unit with the lot it belonged to when it started operation. However, the return data is in terms of usage and not date of return. Therefore the usage of the units needs to be specified as a constant usage per unit time or as a distribution. This allows for determining the expected usage of the surviving units.
Suppose that you have been collecting sales (units in service) and returns data. For the returns data, you can determine the number of failures and their usage by reading the odometer value, for example. Determining the number of surviving units (suspensions) and their ages is a straightforward step. By taking the difference between the analysis date and the date when a unit was put in service, you can determine the age of the surviving units.
What is unknown, however, is the exact usage accumulated by each surviving unit. The key part of the usage-based warranty analysis is the determination of the usage of the surviving units based on their age. Therefore, the analyst needs to have an idea about the usage of the product. This can be obtained, for example, from customer surveys or by designing the products to collect usage data. For example, in automotive applications, engineers often use 12,000 miles/year as the average usage. Based on this average, the usage of an item that has been in the field for 6 months and has not yet failed would be 6,000 miles. So to obtain the usage of a suspension based on an average usage, one could take the time of each suspension and multiply it by this average usage. In this situation, the analysis becomes straightforward. With the usage values and the quantities of the returned units, a failure distribution can be constructed and subsequent warranty analysis becomes possible.
Alternatively, and more realistically, instead of using an average usage, an actual distribution that reflects the variation in usage and customer behavior can be used. This distribution describes the usage of a unit over a certain time period (e.g., 1 year, 1 month, etc). This probabilistic model can be used to estimate the usage for all surviving components in service and the percentage of users running the product at different usage rates. In the automotive example, for instance, such a distribution can be used to calculate the percentage of customers that drive 0-200 miles/month, 200-400 miles/month, etc. We can take these percentages and multiply them by the number of suspensions to find the number of items that have been accumulating usage values in these ranges.
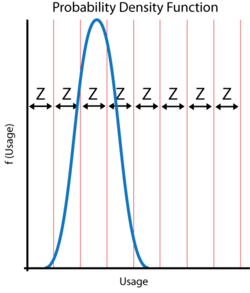
To proceed with applying a usage distribution, the usage distribution is divided into increments based on a specified interval width denoted as [math]\displaystyle{ Z\,\! }[/math]. The usage distribution, [math]\displaystyle{ Q\,\! }[/math], is divided into intervals of [math]\displaystyle{ 0+Z\,\! }[/math], [math]\displaystyle{ Z+Z\,\! }[/math], [math]\displaystyle{ 2Z+Z\,\! }[/math], etc., or [math]\displaystyle{ {{x}_{i}}={{x}_{i-1}}+Z\,\! }[/math], as shown in the next figure.
The interval width should be selected such that it creates segments that are large enough to contain adequate numbers of suspensions within the intervals. The percentage of suspensions that belong to each usage interval is calculated as follows:
- [math]\displaystyle{ \begin{align} F({{x}_{i}})=Q({{x}_{i}})-Q({{x}_{i}}-1) \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ Q()\,\! }[/math] is the usage distribution Cumulative Density Function, cdf.
- [math]\displaystyle{ x\,\! }[/math] represents the intervals used in apportioning the suspended population.
A suspension group is a collection of suspensions that have the same age. The percentage of suspensions can be translated to numbers of suspensions within each interval, [math]\displaystyle{ {{x}_{i}}\,\! }[/math]. This is done by taking each group of suspensions and multiplying it by each [math]\displaystyle{ F({{x}_{i}})\,\! }[/math], or:
- [math]\displaystyle{ \begin{align} & {{N}_{1,j}}= & F({{x}_{1}})\times N{{S}_{j}} \\ & {{N}_{2,j}}= & F({{x}_{2}})\times N{{S}_{j}} \\ & & ... \\ & {{N}_{n,j}}= & F({{x}_{n}})\times N{{S}_{j}} \end{align}\,\! }[/math]
where:
- [math]\displaystyle{ {{N}_{n,j}}\,\! }[/math] is the number of suspensions that belong to each interval.
- [math]\displaystyle{ N{{S}_{j}}\,\! }[/math] is the jth group of suspensions from the data set.
This is repeated for all the groups of suspensions.
The age of the suspensions is calculated by subtracting the Date In-Service ( [math]\displaystyle{ DIS\,\! }[/math] ), which is the date at which the unit started operation, from the end of observation period date or End Date ( [math]\displaystyle{ ED\,\! }[/math] ). This is the Time In-Service ( [math]\displaystyle{ TIS\,\! }[/math] ) value that describes the age of the surviving unit.
- [math]\displaystyle{ \begin{align} TIS=ED-DIS \end{align}\,\! }[/math]
Note: [math]\displaystyle{ TIS\,\! }[/math] is in the same time units as the period in which the usage distribution is defined.
For each [math]\displaystyle{ {{N}_{k,j}}\,\! }[/math], the usage is calculated as:
- [math]\displaystyle{ Uk,j=xi\times TISj\,\! }[/math]
After this step, the usage of each suspension group is estimated. This data can be combined with the failures data set, and a failure distribution can be fitted to the combined data.
Example
Warranty Analysis Usage Format Example
Suppose that an automotive manufacturer collects the warranty returns and sales data given in the following tables. Convert this information to life data and analyze it using the lognormal distribution.
| Quantity In-Service | Date In-Service |
| 9 | Dec-09 |
| 13 | Jan-10 |
| 15 | Feb-10 |
| 20 | Mar-10 |
| 15 | Apr-10 |
| 25 | May-10 |
| 19 | Jun-10 |
| 16 | Jul-10 |
| 20 | Aug-10 |
| 19 | Sep-10 |
| 25 | Oct-10 |
| 30 | Nov-10 |
| Quantity Returned | Usage at Return Date | Date In-Service |
| 1 | 9072 | Dec-09 |
| 1 | 9743 | Jan-10 |
| 1 | 6857 | Feb-10 |
| 1 | 7651 | Mar-10 |
| 1 | 5083 | May-10 |
| 1 | 5990 | May-10 |
| 1 | 7432 | May-10 |
| 1 | 8739 | May-10 |
| 1 | 3158 | Jun-10 |
| 1 | 1136 | Jul-10 |
| 1 | 4646 | Aug-10 |
| 1 | 3965 | Sep-10 |
| 1 | 3117 | Oct-10 |
| 1 | 3250 | Nov-10 |
Solution
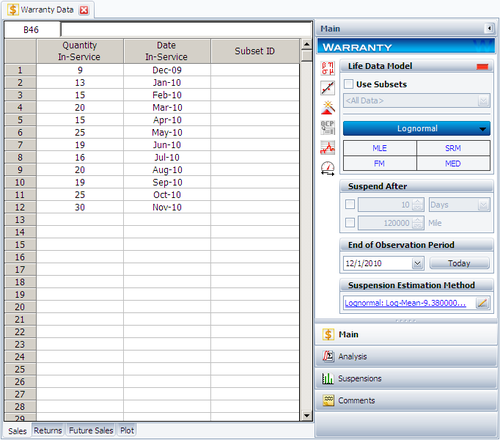
Create a warranty analysis folio and select the usage format. Enter the data from the tables in the Sales, Returns and Future Sales sheets. The warranty data were collected until 12/1/2010; therefore, on the control panel, set the End of Observation Period to that date. Set the failure distribution to Lognormal, as shown next.
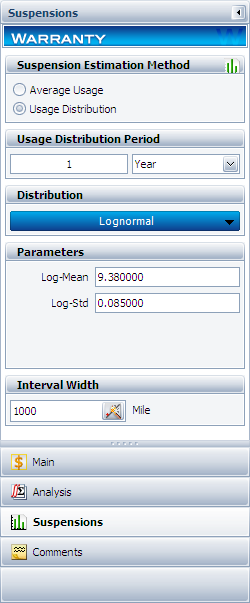
In this example, the manufacturer has been documenting the mileage accumulation per year for this type of product across the customer base in comparable regions for many years. The yearly usage has been determined to follow a lognormal distribution with [math]\displaystyle{ {{\mu }_{T\prime }}=9.38\,\! }[/math], [math]\displaystyle{ {{\sigma }_{T\prime }}=0.085\,\! }[/math]. The Interval Width is defined to be 1,000 miles. Enter the information about the usage distribution on the Suspensions page of the control panel, as shown next.
Click Calculate to analyze the data set. The parameters are estimated to be:
- [math]\displaystyle{ \begin{align} & {{\mu }_{T\prime }}= & 10.528098 \\ & {{\sigma }_{T\prime }}= & 1.135150 \end{align}\,\! }[/math]
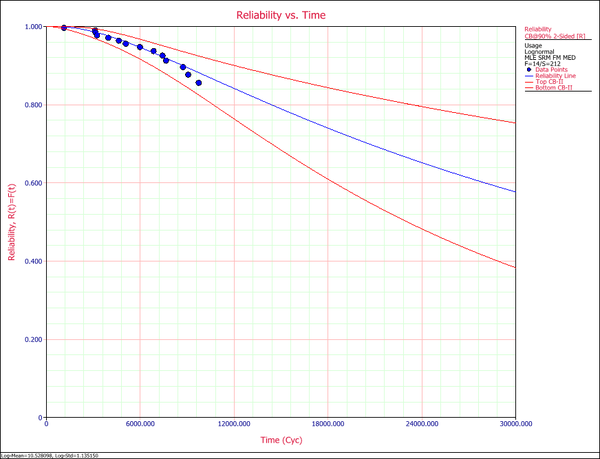
The reliability plot (with mileage being the random variable driving reliability), along with the 90% confidence bounds on reliability, is shown next.
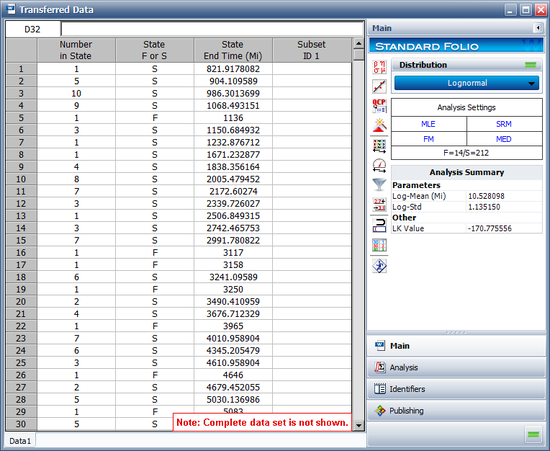
In this example, the life data set contains 14 failures and 212 suspensions spread according to the defined usage distribution. You can display this data in a standard folio by choosing Warranty > Transfer Life Data > Transfer Life Data to New Folio. The failures and suspensions data set, as presented in the standard folio, is shown next (showing only the first 30 rows of data).
To illustrate the calculations behind the results of this example, consider the 9 units that went in service on December 2009. 1 unit failed from that group; therefore, 8 suspensions have survived from December 2009 until the beginning of December 2010, a total of 12 months. The calculations are summarized as follows.
The two columns on the right constitute the calculated suspension data (number of suspensions and their usage) for the group. The calculation is then repeated for each of the remaining groups in the data set. These data are then combined with the data about the failures to form the life data set that is used to estimate the failure distribution model.
Warranty Prediction
Once a life data analysis has been performed on warranty data, this information can be used to predict how many warranty returns there will be in subsequent time periods. This methodology uses the concept of conditional reliability (see Basic Statistical Background) to calculate the probability of failure for the remaining units for each shipment time period. This conditional probability of failure is then multiplied by the number of units at risk from that particular shipment period that are still in the field (i.e., the suspensions) in order to predict the number of failures or warranty returns expected for this time period. The next example illustrates this.
Example
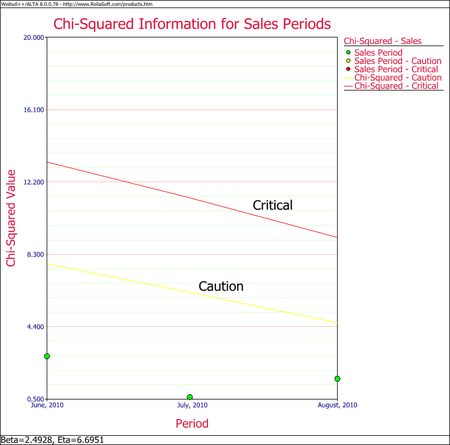
Using the data in the following table, predict the number of warranty returns for October for each of the three shipment periods. Use the following Weibull parameters, beta = 2.4928 and eta = 6.6951.
| RETURNS | ||||
| SHIP | Jul. 2010 | Aug. 2010 | Sep. 2010 | |
| Jun. 2010 | 100 | 3 | 3 | 5 |
| Jul. 2010 | 140 | - | 2 | 4 |
| Aug. 2010 | 150 | - | - | 4 |
Solution
Use the Weibull parameter estimates to determine the conditional probability of failure for each shipment time period, and then multiply that probability with the number of units that are at risk for that period as follows. The equation for the conditional probability of failure is given by:
- [math]\displaystyle{ Q(t|T)=1-R(t|T)=1-\frac{R(T+t)}{R(T)}\,\! }[/math]
For the June shipment, there are 89 units that have successfully operated until the end of September ( [math]\displaystyle{ T=3 months)\,\! }[/math]. The probability of one of these units failing in the next month ( [math]\displaystyle{ t=1 month)\,\! }[/math] is then given by:
- [math]\displaystyle{ Q(1|3)=1-\frac{R(4)}{R(3)}=1-\frac{{{e}^{-{{\left( \tfrac{4}{6.70} \right)}^{2.49}}}}}{{{e}^{-{{\left( \tfrac{3}{6.70} \right)}^{2.49}}}}}=1-\frac{0.7582}{0.8735}=0.132\,\! }[/math]
Once the probability of failure for an additional month of operation is determined, the expected number of failed units during the next month, from the June shipment, is the product of this probability and the number of units at risk ( [math]\displaystyle{ {{S}_{JUN,3}}=89)\,\! }[/math] or:
- [math]\displaystyle{ {{\widehat{F}}_{JUN,4}}=89\cdot 0.132=11.748\text{, or 12 units}\,\! }[/math]
This is then repeated for the July shipment, where there were 134 units operating at the end of September, with an exposure time of two months. The probability of failure in the next month is:
- [math]\displaystyle{ Q(1|2)=1-\frac{R(3)}{R(2)}=1-\frac{0.8735}{0.9519}=0.0824\,\! }[/math]
This value is multiplied by [math]\displaystyle{ {{S}_{JUL,2}}=134\,\! }[/math] to determine the number of failures, or:
- [math]\displaystyle{ {{\widehat{F}}_{JUL,3}}=134\cdot 0.0824=11.035\text{, or 11 units}\,\! }[/math]
For the August shipment, there were 146 units operating at the end of September, with an exposure time of one month. The probability of failure in the next month is:
- [math]\displaystyle{ Q(1|1)=1-\frac{R(2)}{R(1)}=1-\frac{0.9519}{0.9913}=0.0397\,\! }[/math]
This value is multiplied by [math]\displaystyle{ {{S}_{AUG,1}}=146\,\! }[/math] to determine the number of failures, or:
- [math]\displaystyle{ {{\widehat{F}}_{AUG,2}}=146\cdot 0.0397=5.796\text{, or 6 units}\,\! }[/math]
Thus, the total expected returns from all shipments for the next month is the sum of the above, or 29 units. This method can be easily repeated for different future sales periods, and utilizing projected shipments. If the user lists the number of units that are expected be sold or shipped during future periods, then these units are added to the number of units at risk whenever they are introduced into the field. The Generate Forecast functionality in the Weibull++ warranty analysis folio can automate this process for you.
Non-Homogeneous Warranty Data
In the previous sections and examples, it is important to note that the underlying assumption was that the population was homogeneous. In other words, all sold and returned units were exactly the same (i.e., the same population with no design changes and/or modifications). In many situations, as the product matures, design changes are made to enhance and/or improve the reliability of the product. Obviously, an improved product will exhibit different failure characteristics than its predecessor. To analyze such cases, where the population is non-homogeneous, one needs to extract each homogenous group, fit a life model to each group and then project the expected returns for each group based on the number of units at risk for each specific group.
Using Subset IDs in Weibull++
Weibull++ includes an optional Subset ID column that allows to differentiate between product versions or different designs (lots). Based on the entries, the software will separately analyze (i.e., obtain parameters and failure projections for) each subset of data. Note that it is important to realize that the same limitations with regards to the number of failures that are needed are also applicable here. In other words, distributions can be automatically fitted to lots that have return (failure) data, whereas if no returns have been experienced yet (either because the units are going to be introduced in the future or because no failures happened yet), the user will be asked to specify the parameters, since they can not be computed. Consequently, subsequent estimation/predictions related to these lots would be based on the user specified parameters. The following example illustrates the use of Subset IDs.
Example
Warranty Analysis Non-Homogeneous Data Example
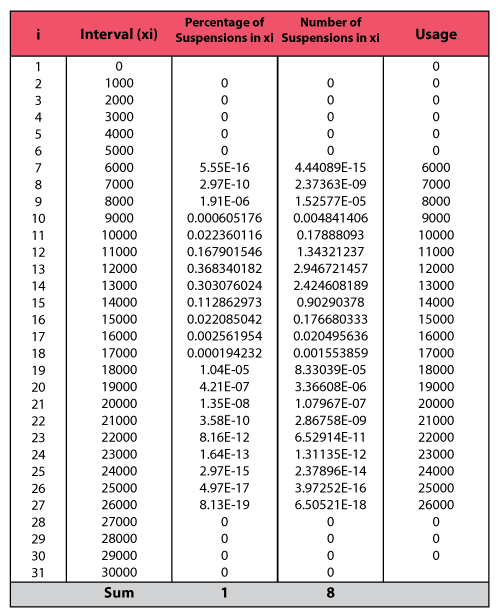
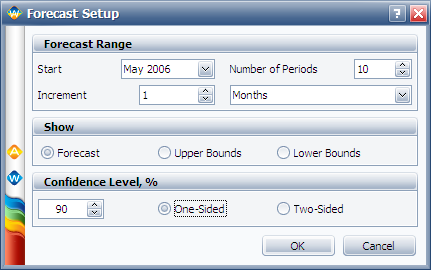
A company keeps track of its production and returns. The company uses the dates of failure format to record the data. For the product in question, three versions (A, B and C) have been produced and put in service. The in-service data is as follows (using the Month/Day/Year date format):
Furthermore, the following sales are forecast:
The return data are as follows. Note that in order to identify which lot each unit comes from, and to be able to compute its time-in-service, each return (failure) includes a return date, the date of when it was put in service and the model ID.
Assuming that the given information is current as of 5/1/2006, analyze the data using the lognormal distribution and MLE analysis method for all models (Model A, Model B, Model C), and provide a return forecast for the next ten months.
Solution
Create a warranty analysis folio and select the dates of failure format. Enter the data from the tables in the Sales, Returns and Future Sales sheets. On the control panel, select the Use Subsets check box, as shown next. This allows the software to separately analyze each subset of data. Use the drop-down list to switch between subset IDs and alter the analysis settings (use the lognormal distribution and MLE analysis method for all models).
In the End of Observation Period field, enter 5/1/2006, and then calculate the parameters. The results are:
Note that in this example, the same distribution and analysis method were assumed for each of the product models. If desired, different distribution types, analysis methods, confidence bounds methods, etc., can be assumed for each IDs.
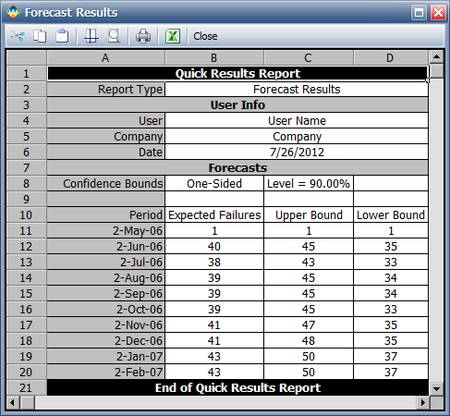
To obtain the expected failures for the next 10 months, click the Generate Forecast icon. In the Forecast Setup window, set the forecast to start on May 2, 2006 and set the number of forecast periods to 10. Set the increment (length of each period) to 1 Month, as shown next.
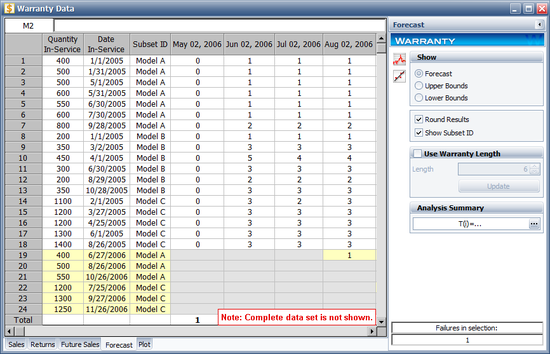
Click OK. A Forecast sheet will be created, with the predicted future returns. The following figure shows part of the Forecast sheet.
To view a summary of the analysis, click the Show Analysis Summary (...) button. The following figure shows the summary of the forecasted returns.
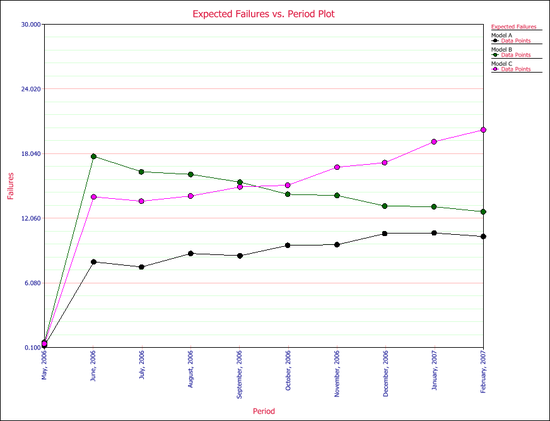
Click the Plot icon and choose the Expected Failures plot. The plot displays the predicted number of returns for each month, as shown next.
Monitoring Warranty Returns Using Statistical Process Control (SPC)
By monitoring and analyzing warranty return data, one can detect specific return periods and/or batches of sales or shipments that may deviate (differ) from the assumed model. This provides the analyst (and the organization) the advantage of early notification of possible deviations in manufacturing, use conditions and/or any other factor that may adversely affect the reliability of the fielded product. Obviously, the motivation for performing such analysis is to allow for faster intervention to avoid increased costs due to increased warranty returns or more serious repercussions. Additionally, this analysis can also be used to uncover different sub-populations that may exist within the population.
Basic Analysis Method
For each sales period [math]\displaystyle{ i\,\! }[/math] and return period [math]\displaystyle{ j\,\! }[/math], the prediction error can be calculated as follows:
- [math]\displaystyle{ {{e}_{i,j}}={{\hat{F}}_{i,j}}-{{F}_{i,j}}\,\! }[/math]
where [math]\displaystyle{ {{\hat{F}}_{i,j}}\,\! }[/math] is the estimated number of failures based on the estimated distribution parameters for the sales period [math]\displaystyle{ i\,\! }[/math] and the return period [math]\displaystyle{ j\,\! }[/math], which is calculated using the equation for the conditional probability, and [math]\displaystyle{ {{F}_{i,j}}\,\! }[/math] is the actual number of failure for the sales period [math]\displaystyle{ i\,\! }[/math] and the return period [math]\displaystyle{ j\,\! }[/math].
Since we are assuming that the model is accurate, [math]\displaystyle{ {{e}_{i,j}}\,\! }[/math] should follow a normal distribution with mean value of zero and a standard deviation [math]\displaystyle{ s\,\! }[/math], where:
- [math]\displaystyle{ {{\bar{e}}_{i,j}}=\frac{\underset{i}{\mathop{\sum }}\,\underset{j}{\mathop{\sum }}\,{{e}_{i,j}}}{n}=0\,\! }[/math]
and [math]\displaystyle{ n\,\! }[/math] is the total number of return data (total number of residuals).
The estimated standard deviation of the prediction errors can then be calculated by:
- [math]\displaystyle{ s=\sqrt{\frac{1}{n-1}\underset{i}{\mathop \sum }\,\underset{j}{\mathop \sum }\,e_{i,j}^{2}}\,\! }[/math]
and [math]\displaystyle{ {{e}_{i,j}}\,\! }[/math] can be normalized as follows:
- [math]\displaystyle{ {{z}_{i,j}}=\frac{{{e}_{i,j}}}{s}\,\! }[/math]
where [math]\displaystyle{ {{z}_{i,j}}\,\! }[/math] is the standardized error. [math]\displaystyle{ {{z}_{i,j}}\,\! }[/math] follows a normal distribution with [math]\displaystyle{ \mu =0\,\! }[/math] and [math]\displaystyle{ \sigma =1\,\! }[/math].
It is known that the square of a random variable with standard normal distribution follows the [math]\displaystyle{ {{\chi }^{2}}\,\! }[/math] (Chi Square) distribution with 1 degree of freedom and that the sum of the squares of [math]\displaystyle{ m\,\! }[/math] random variables with standard normal distribution follows the [math]\displaystyle{ {{\chi }^{2}}\,\! }[/math] distribution with [math]\displaystyle{ m\,\! }[/math] degrees of freedom. This then can be used to help detect the abnormal returns for a given sales period, return period or just a specific cell (combination of a return and a sales period).
- For a cell, abnormality is detected if [math]\displaystyle{ z_{i,j}^{2}=\chi _{1}^{2}\ge \chi _{1,\alpha }^{2}.\,\! }[/math]
- For an entire sales period [math]\displaystyle{ i\,\! }[/math], abnormality is detected if [math]\displaystyle{ \underset{j}{\mathop{\sum }}\,z_{i,j}^{2}=\chi _{J}^{2}\ge \chi _{\alpha ,J}^{2},\,\! }[/math] where [math]\displaystyle{ J\,\! }[/math] is the total number of return period for a sales period [math]\displaystyle{ i\,\! }[/math].
- For an entire return period [math]\displaystyle{ j\,\! }[/math], abnormality is detected if [math]\displaystyle{ \underset{i}{\mathop{\sum }}\,z_{i,j}^{2}=\chi _{I}^{2}\ge \chi _{\alpha ,I}^{2},\,\! }[/math] where [math]\displaystyle{ I\,\! }[/math] is the total number of sales period for a return period [math]\displaystyle{ j\,\! }[/math].
Here [math]\displaystyle{ \alpha \,\! }[/math] is the criticality value of the [math]\displaystyle{ {{\chi }^{2}}\,\! }[/math] distribution, which can be set at critical value or caution value. It describes the level of sensitivity to outliers (returns that deviate significantly from the predictions based on the fitted model). Increasing the value of [math]\displaystyle{ \alpha \,\! }[/math] increases the power of detection, but this could lead to more false alarms.
Example
Example Using SPC for Warranty Analysis Data
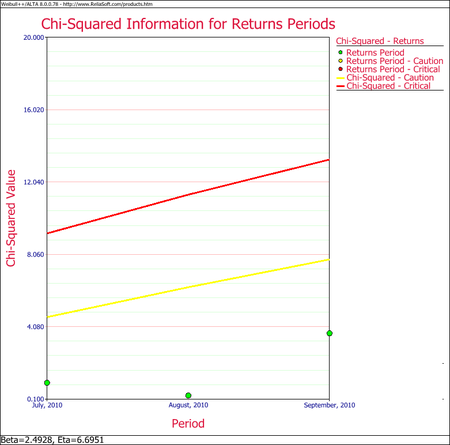
Using the data from the following table, the expected returns for each sales period can be obtained using conditional reliability concepts, as given in the conditional probability equation.
| RETURNS | ||||
| SHIP | Jul. 2010 | Aug. 2010 | Sep. 2010 | |
| Jun. 2010 | 100 | 3 | 3 | 5 |
| Jul. 2010 | 140 | - | 2 | 4 |
| Aug. 2010 | 150 | - | - | 4 |
For example, for the month of September, the expected return number from the June shipment is given by:
- [math]\displaystyle{ {{\hat{F}}_{Jun,3}}=(100-6)\cdot \left( 1-\frac{R(3)}{R(2)} \right)=94\cdot 0.08239=7.7447\,\! }[/math]
The actual number of returns during this period is five; thus, the prediction error for this period is:
- [math]\displaystyle{ {{e}_{Jun,3}}={{\hat{F}}_{Jun,3}}-{{F}_{Jun,3}}=7.7447-5=2.7447.\,\! }[/math]
This can then be repeated for each cell, yielding the following table for [math]\displaystyle{ {{e}_{i,j}}\,\! }[/math] :
Now, for this example, [math]\displaystyle{ n=6\,\! }[/math], [math]\displaystyle{ {{\bar{e}}_{i,j}}=-0.0904\,\! }[/math] and [math]\displaystyle{ s=2.1366.\,\! }[/math]
Thus the [math]\displaystyle{ z_{i,j}\,\! }[/math] values are:
The [math]\displaystyle{ z_{i,j}^{2}\,\! }[/math] values, for each cell, are given in the following table.
If the critical value is set at [math]\displaystyle{ \alpha = 0.01\,\! }[/math] and the caution value is set at [math]\displaystyle{ \alpha = 0.1\,\! }[/math], then the critical and caution [math]\displaystyle{ {{\chi }^{2}}\,\! }[/math] values will be:
If we consider the sales periods as the basis for outlier detection, then after comparing the above table to the sum of [math]\displaystyle{ z_{i,j}^{2}\,\! }[/math] [math]\displaystyle{ (\chi _{1}^{2})\,\! }[/math] values for each sales period, we find that all the sales values do not exceed the critical and caution limits. For example, the total [math]\displaystyle{ {{\chi }^{2}}\,\! }[/math] value of the sale month of July is 0.6085. Its degrees of freedom is 2, so the corresponding caution and critical values are 4.6052 and 9.2103 respectively. Both values are larger than 0.6085, so the return numbers of the July sales period do not deviate (based on the chosen significance) from the model's predictions.
If we consider returns periods as the basis for outliers detection, then after comparing the above table to the sum of [math]\displaystyle{ z_{i,j}^{2}\,\! }[/math] [math]\displaystyle{ (\chi _{1}^{2})\,\! }[/math] values for each return period, we find that all the return values do not exceed the critical and caution limits. For example, the total [math]\displaystyle{ {{\chi }^{2}}\,\! }[/math] value of the sale month of August is 3.7157. Its degree of freedom is 3, so the corresponding caution and critical values are 6.2514 and 11.3449 respectively. Both values are larger than 3.7157, so the return numbers for the June return period do not deviate from the model's predictions.
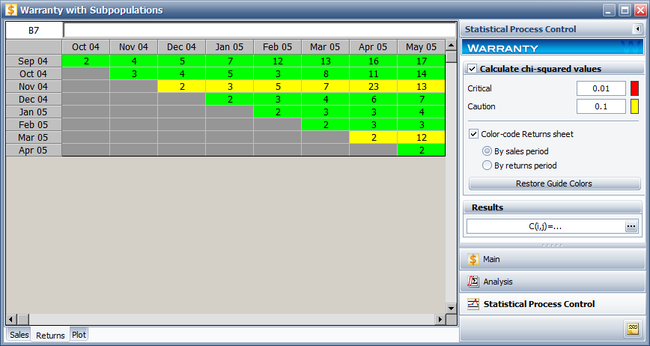
This analysis can be automatically performed in Weibull++ by entering the alpha values in the Statistical Process Control page of the control panel and selecting which period to color code, as shown next.
To view the table of chi-squared values ( [math]\displaystyle{ z_{i,j}^{2}\,\! }[/math] or [math]\displaystyle{ \chi _{1}^{2}\,\! }[/math] values), click the Show Results (...) button.
Weibull++ automatically color codes SPC results for easy visualization in the returns data sheet. By default, the green color means that the return number is normal; the yellow color indicates that the return number is larger than the caution threshold but smaller than the critical value; the red color means that the return is abnormal, meaning that the return number is either too big or too small compared to the predicted value.
In this example, all the cells are coded in green for both analyses (i.e., by sales periods or by return periods), indicating that all returns fall within the caution and critical limits (i.e., nothing abnormal). Another way to visualize this is by using a Chi-Squared plot for the sales period and return period, as shown next.
Using Subset IDs with SPC for Warranty Data
The warranty monitoring methodology explained in this section can also be used to detect different subpopulations in a data set. The different subpopulations can reflect different use conditions, different material, etc. In this methodology, one can use different subset IDs to differentiate between subpopulations, and obtain models that are distinct to each subpopulation. The following example illustrates this concept.
Example
Using Subset IDs with Statistical Process Control
A manufacturer wants to monitor and analyze the warranty returns for a particular product. They collected the following sales and return data.
Solution
Analyze the data using the two-parameter Weibull distribution and the MLE analysis method. The parameters are estimated to be:
- [math]\displaystyle{ \begin{align} & & \beta = & 2.318144 \\ & & \eta = & 25.071878 \end{align}\,\! }[/math]
To analyze the warranty returns, select the check box in the Statistical Process Control page of the control panel and set the alpha values to 0.01 for the Critical Value and 0.1 for the Caution Value. Select to color code the results By sales period. The following figure shows the analysis settings and results of the analysis.
As you can see, the November 04 and March 05 sales periods are colored in yellow indicating that they are outlier sales periods, while the rest are green. One suspected reason for the variation may be the material used in production during these periods. Further analysis confirmed that for these periods, the material was acquired from a different supplier. This implies that the units are not homogenous, and that there are different sub-populations present in the field population.
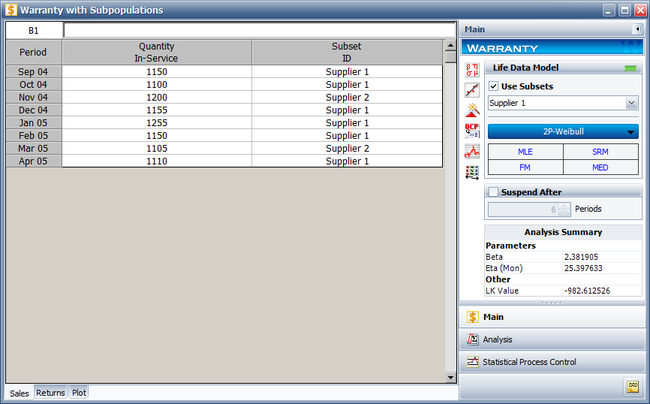
Categorized each shipment (using the Subset ID column) based on their material supplier, as shown next. On the control panel, select the Use Subsets check box. Perform the analysis again using the two-parameter Weibull distribution and the MLE analysis method for both sub-populations.
The new models that describe the data are:
This analysis uncovered different sub-populations in the data set. Note that if the analysis were performed on the failure and suspension times in a regular standard folio using the mixed Weibull distribution, one would not be able to detect which units fall into which sub-population.