Arrhenius-Lognormal Model for Interval Data: Difference between revisions
Jump to navigation
Jump to search
Kate Racaza (talk | contribs) No edit summary |
Kate Racaza (talk | contribs) No edit summary |
||
| (5 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Reference Example| | {{Reference Example|{{Banner ALTA Reference Examples}}}} | ||
This example | This example validates the results for the Arrhenius-lognormal model with interval data in ALTA standard folios. | ||
| Line 11: | Line 11: | ||
{{Reference_Example_Heading2}} | {{Reference_Example_Heading2}} | ||
The data set for a new-technology IC | The data set for a new-technology IC device is given below. | ||
{| {{table}} | {| {{table}} | ||
| Line 48: | Line 48: | ||
where ''T'' is the temperature; <math>\beta_{1}\,\!</math> is the activation energy; 11605 is calculated from the reciprocal of the Boltzmann constant. This function can be written in the following way: | where ''T'' is the temperature; <math>\beta_{1}\,\!</math> is the activation energy; and 11605 is calculated from the reciprocal of the Boltzmann constant. This function can be written in the following way: | ||
::<math>e^{\mu'} = e^{\alpha_{0}+ \frac {\alpha_{1}}{T}}\,\!</math> | ::<math>e^{\mu'} = e^{\alpha_{0}+ \frac {\alpha_{1}}{T}}\,\!</math> | ||
The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by <math>\alpha_{i}\,\!</math>. We can see <math>\beta_{0} = \alpha_{0}\,\!</math> and <math>\beta_{1} = \frac{\alpha_{1}}{11605}\,\!</math>. | The above equation is the general log-linear model in ALTA. In ALTA, the coefficients are denoted by <math>\alpha_{i}\,\!</math>. We can see that <math>\beta_{0} = \alpha_{0}\,\!</math> and <math>\beta_{1} = \frac{\alpha_{1}}{11605}\,\!</math>. | ||
In fact, the above model also | In fact, the above model can also be expressed using the traditional Arrhenius model: | ||
::<math>e^{\mu'} = e^{\alpha_{0}+ \frac {\alpha_{1}}{T}} = C \times e^{\frac{B}{T}}\,\!</math> | ::<math>e^{\mu'} = e^{\alpha_{0}+ \frac {\alpha_{1}}{T}} = C \times e^{\frac{B}{T}}\,\!</math> | ||
| Line 63: | Line 62: | ||
In the book, the following results are provided: | In the book, the following results are provided: | ||
* ML estimations for the model parameters are: <math>\sigma\,\!</math> = 0.52, <math>\beta_{0}\,\!</math> = -10.2, <math>\beta_{1}\,\!</math> = 0.83, (<math>\alpha_{1}\,\!</math> = <math>\beta_{1}\times \,\!</math> 11605 = 9632.15). | * The ML estimations for the model parameters are: <math>\sigma\,\!</math> = 0.52, <math>\beta_{0}\,\!</math> = -10.2, <math>\beta_{1}\,\!</math> = 0.83, (<math>\alpha_{1}\,\!</math> = <math>\beta_{1}\times \,\!</math> 11605 = 9632.15). | ||
* The standard deviation of each parameter: <math>std(\sigma)\,\!</math> = 0.06, <math>std(\beta_{0})\,\!</math> = 1.5, <math>std(\beta_{1})\,\!</math> = 0.07. Therefore, their variances are: <math>Var(\sigma)\,\!</math> = 0.0036, <math>Var(\beta_{0})\,\!</math> = 2.25, <math>Var(\beta_{1})\,\!</math> = 0.0049. In terms of <math>\alpha_{1}\,\!</math> , the variance is <math>Var(\alpha_{1})\,\!</math> = 11605<sup>2</sup> and <math>Var(\beta_{1})\,\!</math> = 659912.5. | * The standard deviation of each parameter: <math>std(\sigma)\,\!</math> = 0.06, <math>std(\beta_{0})\,\!</math> = 1.5, <math>std(\beta_{1})\,\!</math> = 0.07. Therefore, their variances are: <math>Var(\sigma)\,\!</math> = 0.0036, <math>Var(\beta_{0})\,\!</math> = 2.25, <math>Var(\beta_{1})\,\!</math> = 0.0049. In terms of <math>\alpha_{1}\,\!</math> , the variance is <math>Var(\alpha_{1})\,\!</math> = 11605<sup>2</sup> and <math>Var(\beta_{1})\,\!</math> = 659912.5. | ||
* The 95% two-sided confidence bounds are: for <math>\sigma\,\!</math> it is [0.42, 0.64]; for <math>\beta_{0}\,\!</math> it is [-13.2, -7.2]; for <math>\beta_{1}\,\!</math> it is [0.68, 0.97]. In terms of <math>\alpha_{1}\,\!</math>, the bounds are [7891.14, 11256.85]. | * The 95% two-sided confidence bounds are: for <math>\sigma\,\!</math> it is [0.42, 0.64]; for <math>\beta_{0}\,\!</math> it is [-13.2, -7.2]; for <math>\beta_{1}\,\!</math> it is [0.68, 0.97]. In terms of <math>\alpha_{1}\,\!</math>, the bounds are [7891.14, 11256.85]. | ||
| Line 71: | Line 70: | ||
{{Reference_Example_Heading4|ALTA}} | {{Reference_Example_Heading4|ALTA}} | ||
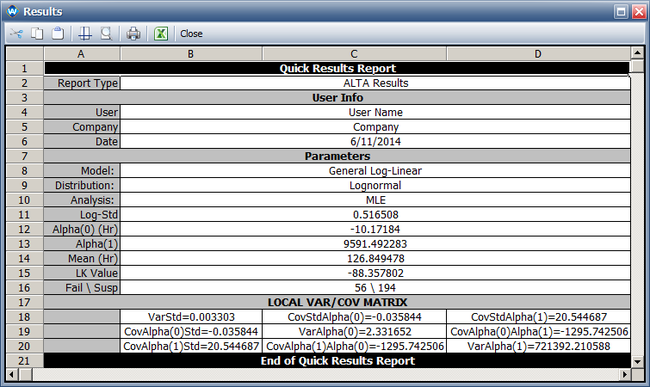
* The following picture shows the ML estimations for the model parameters in ALTA and the log-likelihood value (LK Value). | |||
[[Image: Arrhenius Log results.png|center|650px]] | |||
The picture above also shows variance of each parameter. These are: <math>Var(\sigma)\,\!</math> = 0.003303, <math>Var(\alpha_{0})\,\!</math> = 2.331652, <math>Var(\alpha_{1})\,\!</math> = 721392.210588. In terms of <math>\beta_{1}\,\!</math> , the variance is <math>Var(\beta_{1}) = \frac{Var(\alpha_{1})}{11605^{2}}\,\!</math> = 0.0053565. | |||
The differences in the variance in ALTA and the results in the book are caused by the precision in the book since results are provided only up to the 2nd decimal. | |||
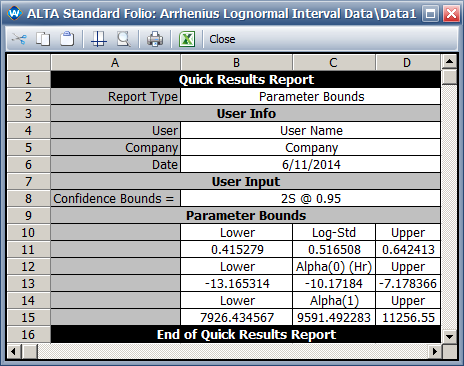
* The 95% two-sided confidence bounds on the parameters are shown next: | |||
[[Image: Arrhenius Log parameter bounds.png|center]] | |||
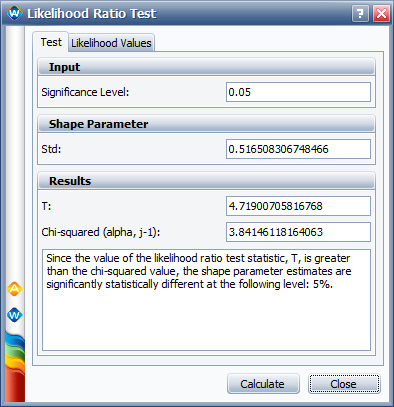
* The likelihood ratio common shape parameter test statistic is 4.7, as shown next. | |||
[[Image: Arrhenius Log LK test.png|center]] | |||
As the results show, the values obtained by ALTA are very close to the results given in the book. | |||
Latest revision as of 18:18, 28 September 2015
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.