Weibull-Bayesian with Prior Information on Beta: Difference between revisions
Jump to navigation
Jump to search
Kate Racaza (talk | contribs) (Created page with '{{Reference Example}} This example compares the Weibull-Bayesian calculation. {{Reference_Example_Heading1}} The data from Example 14.1 on page 348 in the book ''Statistical …') |
Kate Racaza (talk | contribs) No edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{Reference Example}} | {{Reference Example}} | ||
This example | This example validates the Weibull-Bayesian calculations in Weibull++ standard folios. | ||
{{Reference_Example_Heading1}} | {{Reference_Example_Heading1}} | ||
The data from Example 14.1 on page 348 in the book ''Statistical Methods for Reliability Data'' by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998 is used. | The data set from Example 14.1 on page 348 in the book ''Statistical Methods for Reliability Data'' by Dr. Meeker and Dr. Escobar, John Wiley & Sons, 1998 is used. | ||
| Line 81: | Line 81: | ||
{{Reference_Example_Heading4}} | {{Reference_Example_Heading4}} | ||
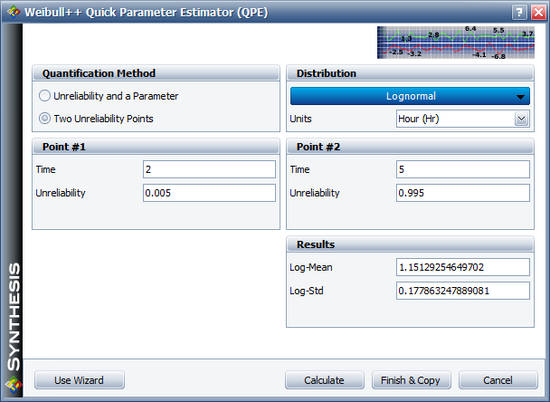
In Weibull++, the prior distribution is set for <math>\beta\,\!</math> directly. Based on the information of <math>\sigma\,\!</math>, we know <math>\beta_{0.005}\,\!</math> = 2 and <math>\beta_{0.995}\,\!</math> = 5. Therefore, we can get the prior lognormal distribution for <math>\beta\,\!</math>. | In Weibull++, the prior distribution is set for <math>\beta\,\!</math> directly. Based on the information of <math>\sigma\,\!</math>, we know <math>\beta_{0.005}\,\!</math> = 2 and <math>\beta_{0.995}\,\!</math> = 5. Therefore, we can use the Quick Parameter Estimator (QPE) to get the prior lognormal distribution for <math>\beta\,\!</math>. The results are Log-Mean = 1.15129 and Log-Std = 0.17786, as shown next. | ||
[[Image: | [[Image:WeiBays_QPE.png|center|550px|]] | ||
Applying this prior distribution for Wei-Bayesian, we have the following results: | Applying this prior distribution for Wei-Bayesian, we have the following results: | ||
| Line 89: | Line 89: | ||
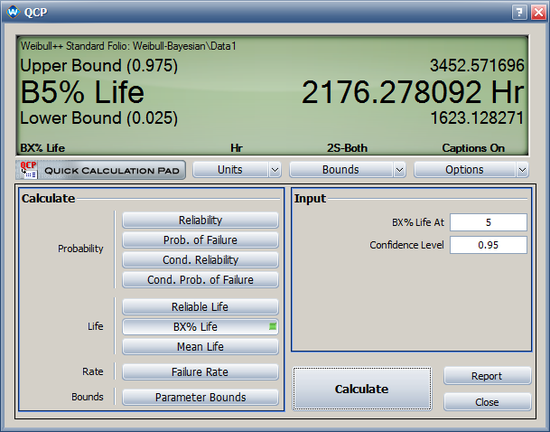
* The 95% two-sided Bayesian confidence interval for <math>t_{0.05}\,\!</math> (B5% life) is [1623, 3452]. | * The 95% two-sided Bayesian confidence interval for <math>t_{0.05}\,\!</math> (B5% life) is [1623, 3452]. | ||
[[Image: | [[Image:WeiBays_B5.png|center|550px|]] | ||
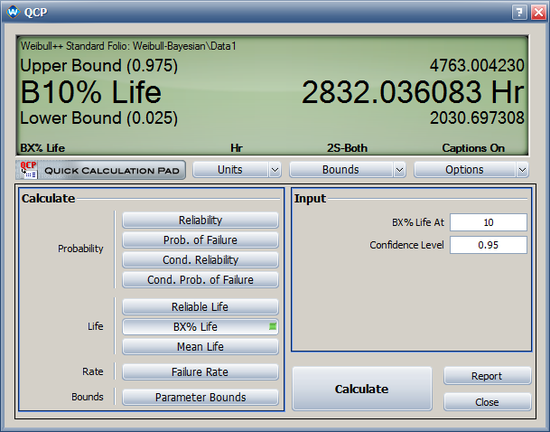
* The 95% two-sided Bayesian confidence interval for <math>t_{0.10}\,\!</math> (B10% life) is [2030, 4763]. | * The 95% two-sided Bayesian confidence interval for <math>t_{0.10}\,\!</math> (B10% life) is [2030, 4763]. | ||
[[Image: | [[Image:WeiBays_B10.png|center|550px|]] | ||
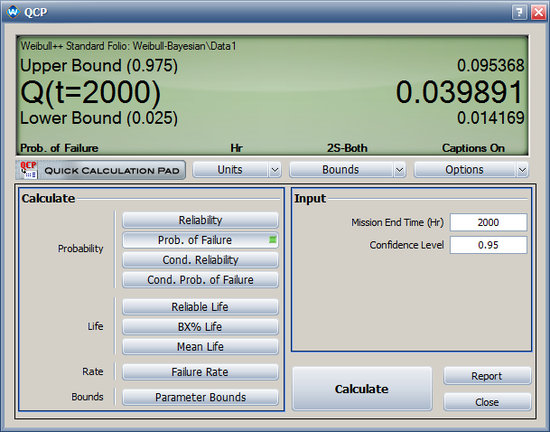
* The 95% two-sided Bayesian confidence interval for F(2000) (probability of failure at time of 2000) is [0.014, 0.095]. | * The 95% two-sided Bayesian confidence interval for F(2000) (probability of failure at time of 2000) is [0.014, 0.095]. | ||
[[Image: | [[Image:WeiBays_F2000.png|center|550px|]] | ||
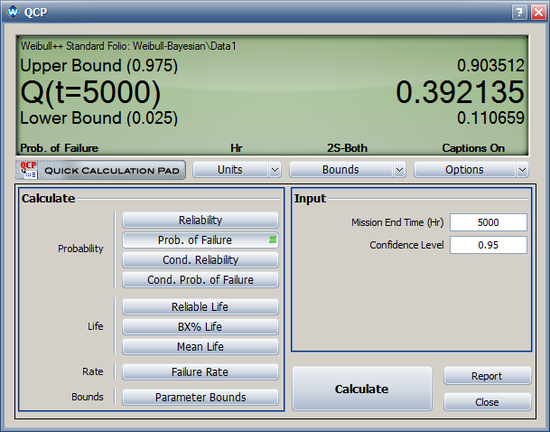
* The 95% two-sided Bayesian confidence interval for F(5000) (probability of failure at time of 5000) is [0.111, 0.903]. | * The 95% two-sided Bayesian confidence interval for F(5000) (probability of failure at time of 5000) is [0.111, 0.903]. | ||
[[Image: | [[Image:WeiBays_F5000.png|center|550px|]] | ||
The results in Weibull++ are very close | The results in Weibull++ are very close but not exactly the same as the results in the book. The differences are mainly caused by the fact that the prior lognormal distribution is for <math>\sigma\,\!</math> in the book while it is for <math>\beta\,\!</math> in Weibull++. | ||
Latest revision as of 16:21, 28 September 2015
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.