Median Rank for Multiple Censored Data: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
 
(2 intermediate revisions by the same user not shown)
Line 1: Line 1:
{{Reference Example}}
{{Reference Example}}


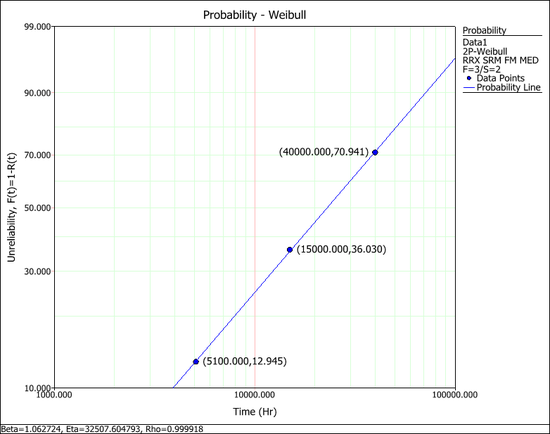
This example compares the median rank calculation for multiple censored data.
This example validates the median rank calculation for multiple censored data in Weibull++ standard folios.




{{Reference Example Heading1}}
{{Reference Example Heading1}}
Table 3.1 on page 78 in the book “''Reliability & Life Testing Handbook Vol 2''” by Dr. Kececioglu, Prentice-Hall, 1994.
Table 3.1 on page 78 in the book ''Reliability & Life Testing Handbook Vol 2'' by Dr. Kececioglu, Prentice-Hall, 1994.




Line 53: Line 53:




The differences between the results in Weibull++ and the book are due to the method of calculating the median ranks (MR). In the book, the following approximation method is used.
The differences between the results in Weibull++ and the book are due to the method of calculating the median ranks (MR). In the book, the following approximation method is used:


::<math>MR_{i}\approx \frac{MON_{i}-0.3}{N+0.4}</math>
::<math>MR_{i}\approx \frac{MON_{i}-0.3}{N+0.4}</math>
Line 61: Line 61:




In Weibull++, the following exact method is used.
In Weibull++, the following exact method is used:


::<math>MR_{i}= \frac{1}{1+\frac{N-MON_{i}+1}{MON_{i}}F_{0.5,m,n}}</math>
::<math>MR_{i}= \frac{1}{1+\frac{N-MON_{i}+1}{MON_{i}}F_{0.5,m,n}}</math>


   
   
where <math>m=2(N-MON_{i}+1), n=2xMON_{i}\cdot F_{0.5,m,n}\,\!</math> is the 50 percentile of a F distribution with degree of freedom of ''m'' and ''n''.
where <math>m=2(N-MON_{i}+1), n=2\times MON_{i}\cdot F_{0.5,m,n}\,\!</math> is the 50 percentile of a F distribution with degree of freedom of ''m'' and ''n''.

Latest revision as of 16:20, 28 September 2015

Weibull Reference Examples Banner.png


New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.



Median Rank for Multiple Censored Data

This example validates the median rank calculation for multiple censored data in Weibull++ standard folios.


Reference Case

Table 3.1 on page 78 in the book Reliability & Life Testing Handbook Vol 2 by Dr. Kececioglu, Prentice-Hall, 1994.


Data

Num. In Stage State F or S Time to Failure
1 F 5100
1 S 9500
1 F 15000
1 S 22000
1 F 40000


Result

Num. In Stage State F or S Time to Failure Median Rank (%)
1 F 5100 12.94
1 S 9500
1 F 15000 36.1
1 S 22000
1 F 40000 70.84


Results in Weibull++

The coordinates of each point in the following plot shows the failure time and the corresponding median rank.


Median Ranks Multiple Censored Data.png


The differences between the results in Weibull++ and the book are due to the method of calculating the median ranks (MR). In the book, the following approximation method is used:

[math]\displaystyle{ MR_{i}\approx \frac{MON_{i}-0.3}{N+0.4} }[/math]


where [math]\displaystyle{ MR_{i}\,\! }[/math] is the median rank at the [math]\displaystyle{ ith\,\! }[/math] failure time; [math]\displaystyle{ MON_{i}\,\! }[/math] is the mean order number; [math]\displaystyle{ N\,\! }[/math] is the total samples. For the step by step calculation of mean order number (MON), please refer to the book “Reliability & Life Testing Handbook Vol 2” by Dr. Kececioglu, Prentice-Hall, 1994.


In Weibull++, the following exact method is used:

[math]\displaystyle{ MR_{i}= \frac{1}{1+\frac{N-MON_{i}+1}{MON_{i}}F_{0.5,m,n}} }[/math]


where [math]\displaystyle{ m=2(N-MON_{i}+1), n=2\times MON_{i}\cdot F_{0.5,m,n}\,\! }[/math] is the 50 percentile of a F distribution with degree of freedom of m and n.

Retrieved from "https://www.reliawiki.com/index.php?title=Median_Rank_for_Multiple_Censored_Data&oldid=60816"