Three Level Compromise Test Plan for One Stress: Difference between revisions
Jump to navigation
Jump to search
Kate Racaza (talk | contribs) (Created page with '{{Reference Example|ALTA_Reference_Examples_Banner.png|ALTA_Reference_Examples}} This example compares the statistically optimum test plan result for one stress from the ALTA Te…') |
Kate Racaza (talk | contribs) No edit summary |
||
| Line 37: | Line 37: | ||
* 84 units will be tested at temperature of 120°C (393.15°K) | * 84 units will be tested at temperature of 120°C (393.15°K) | ||
The estimated standard error for the B10 life at 50°C from this test plan is <math>Ase\left [log \left(\hat{t}_{0.1}(50) \right) \right]\,\!</math> . | The estimated standard error for the B10 life at 50°C from this test plan is <math>Ase\left [log \left(\hat{t}_{0.1}(50) \right) \right] = 0.4375\,\!</math> . | ||
{{Reference_Example_Heading4|ALTA}} | {{Reference_Example_Heading4|ALTA}} | ||
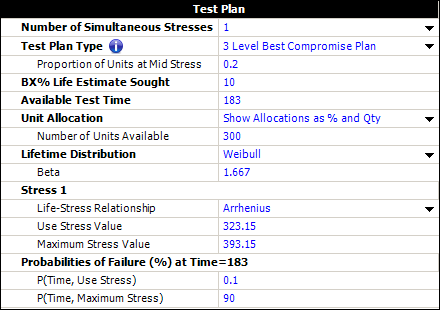
The planning information is entered in ALTA, as shown below. | |||
[[Image: Compromise plan one stress.png|center]] | |||
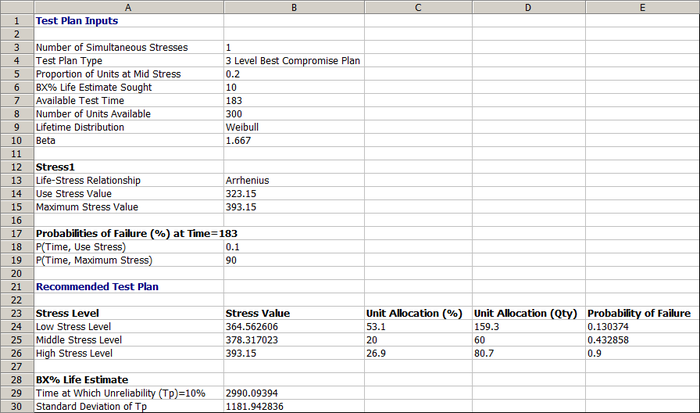
The resulting three level best compromise test plan in ALTA is shown below. | |||
[[Image: Compromise plan test plan.png|center|700 px]] | |||
The test plan shows that: | |||
* The low stress level (row 29) should be 364.56 °K (91.41°C) and about 159 units should be tested at this temperature. | |||
* The middle stress level (row 30) should be 378.32 °K (105.17°C) and about 60 units should be tested at this temperature. | |||
* The high stress level (row 31) should be 393.15 °K (120°C) and about 81 units should be tested at this temperature. | |||
The estimated standard deviation of the log B10 life at 50°C can be obtained by: | |||
::<math>Ase\left[log \left(\hat{t}_{0.1}(50) \right) \right] = \frac{Ase\hat{t}_{0.1}(50)}{\hat{t}_{0.1}(50)} = \frac{1181.94}{2990.09} = 0.3953\,\!</math> | |||
The above results are different from the results in the book. In the following discussion, a simulation study is conducted to check the result obtained from ALTA. | |||
'''Using ALTA SimuMatic to Evaluate the Test Plan''' | |||
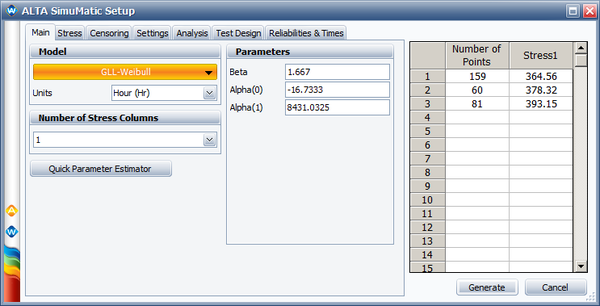
We will use the SimuMatic utility to evaluate the test plan. The following picture shows the settings used the Main tab of SimuMatic (with <math>\alpha_{1} = \beta_{1} \times 11605\,\!</math>): | |||
[[Image: Compromise plan simumatic.png|center|600px]] | |||
The rest of the SimuMatic settings are as follows: | |||
* Stress tab: | |||
::Use level = '''323.15''', Transformation = '''Reciprocal''' | |||
* Censoring tab: | |||
::Right censoring after time '''183'''. | |||
* Settings tab | |||
::Seed = '''10''', Precision = '''4''', Number of data sets = '''1000''' | |||
* Reliabilities and Times | |||
::Reliability value = '''0.9''' | |||
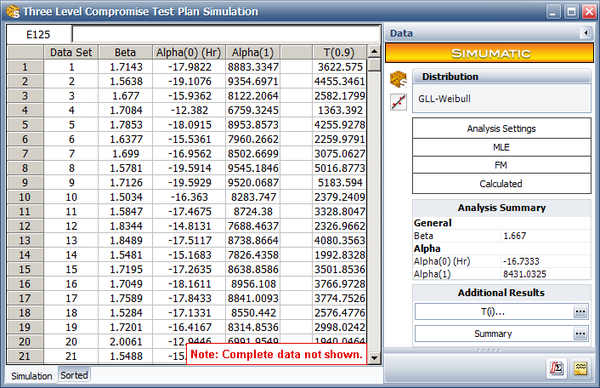
The simulation results are shown next. | |||
[[Image: Compromise plan simumatic2.png|center|600px]] | |||
We take the nature log of the B10 life (the last column) and calculate its standard deviation. The calculated standard deviation is 0.4062. This is very close to the analytical solution from the ALTA test plan tool, where the standard deviation is 0.3953. | |||
This standard deviation is smaller than the standard deviation given by the test plan in the book. Therefore, the test plan generated in ALTA is better than the test plan given in the book in terms of minimizing the estimation variance of the B10 life. | |||
Revision as of 17:46, 11 June 2014
ALTA_Reference_Examples_Banner.png