Arrhenius-Exponential Model: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
No edit summary
Line 31: Line 31:
{{Reference_Example_Heading3}}
{{Reference_Example_Heading3}}


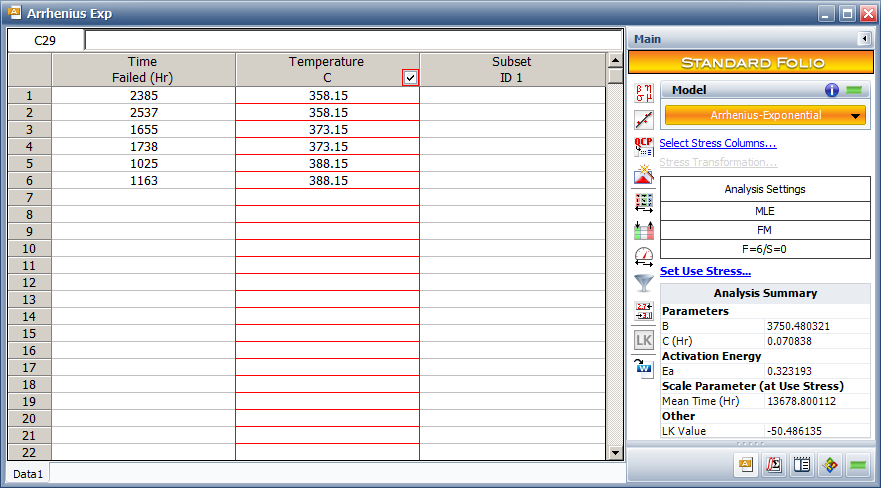
For this data set, the Arrhenius life stress relationship with an Exponential distribution is used.  The estimated activation energy value is <math>\,\!E_{a}=0.323</math>. The acceleration factor from 70 °C to 35 °C is 3.5.
For this data set, the Arrhenius life stress relationship with an Exponential distribution is used.  The estimated activation energy value is <math>\,\!E_{a}=0.323</math>. The acceleration factor from 70°C to 35°C is 3.5.




Line 39: Line 39:


[[image:Arrhenius Exp_Folio.png|center]]
[[image:Arrhenius Exp_Folio.png|center]]
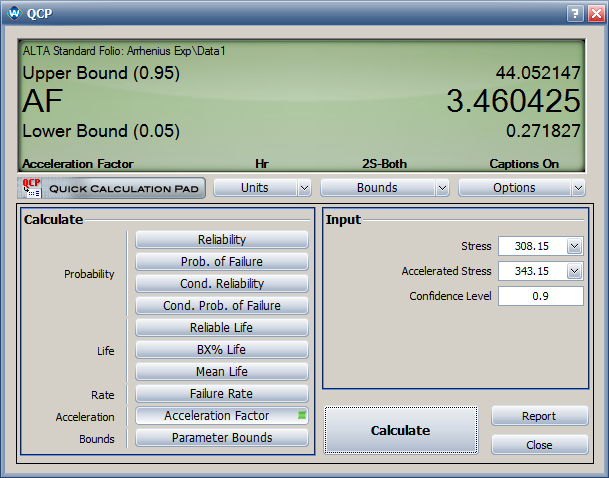
The calculated activation energy is 0.323. The acceleration factor from 70°C (343.15°K) to 35°C (308.15°K) is 3.46 as given below.
[[image:Arrhenius Exp_QPC.png|center]]

Revision as of 23:15, 9 June 2014

ALTA_Reference_Examples_Banner.png

ALTA_Reference_Examples

Validate the calculation of Arrhenius-Exponential model.

Reference Case

Data is from Example 7.1 on page 254 in book Life Cycle Reliability Engineering by Dr. Guangbin Yang, John Wiley & Sons, 2007.


Data

Failure Time Temperature (°C)
2385 85
2537 85
1655 100
1738 100
1025 115
1163 115


Result

For this data set, the Arrhenius life stress relationship with an Exponential distribution is used. The estimated activation energy value is [math]\displaystyle{ \,\!E_{a}=0.323 }[/math]. The acceleration factor from 70°C to 35°C is 3.5.


Results in ALTA

In ALTA, the temperature values are converted from degree C to degree K.

Arrhenius Exp Folio.png

The calculated activation energy is 0.323. The acceleration factor from 70°C (343.15°K) to 35°C (308.15°K) is 3.46 as given below.

Arrhenius Exp QPC.png
Retrieved from "https://www.reliawiki.com/index.php?title=Arrhenius-Exponential_Model&oldid=55408"