Operational Testing Example: Difference between revisions
Chris Kahn (talk | contribs) No edit summary |
Chris Kahn (talk | contribs) No edit summary |
||
| Line 74: | Line 74: | ||
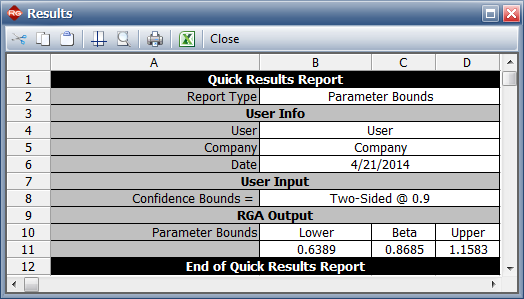
The assumption of <math>\beta = 1\,\!</math> can be verified by looking at the confidence bounds on <math>\beta\,\!</math> via the Quick Calculation Pad (QCP). The 90% 2-sided Crow confidence bounds on <math>\beta\,\!</math> are shown next. | The assumption of <math>\beta = 1\,\!</math> can be verified by looking at the confidence bounds on <math>\beta\,\!</math> via the Quick Calculation Pad (QCP). The 90% 2-sided Crow confidence bounds on <math>\beta\,\!</math> are shown next. | ||
[[File:OTBeta=1.png|center | [[File:OTBeta=1.png|center|Confidence bounds on Beta.]] | ||
Since the confidence bounds on <math>\beta\,\!</math> include one, then you can fail to reject the hypothesis that <math>\beta = 1\,\!</math>. | Since the confidence bounds on <math>\beta\,\!</math> include one, then you can fail to reject the hypothesis that <math>\beta = 1\,\!</math>. | ||
Revision as of 22:21, 23 April 2014
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.
This example appears in the Reliability Growth and Repairable System Analysis Reference.
Consider two systems that have been placed into operational testing. The data for each system are given below. Do the following:
- After estimating the parameters, verify the assumption of [math]\displaystyle{ \beta = 1\,\! }[/math].
- Estimate the demonstrated MTBF of the system.
- Estimate the MTBF that can be expected after the BD failure modes are addressed (projected MTBF) and the maximum MTBF that can be achieved if all BD modes that exist in the system were discovered and fixed according to the current maintenance strategy (growth potential MTBF).
| System # | 1 | 2 |
| Start Time (Hr) | 0 | 0 |
| End Time (Hr) | 504 | 541 |
| Failure Times (Hr) and Failure Modes |
21 BD43 | 83 BD37 |
| 29 A42 | 83 BD43 | |
| 43 BD10 | 83 BD46 | |
| 43 BD11 | 169 A45 | |
| 43 A39 | 213 A18 | |
| 66 A20 | 299 A42 | |
| 115 BD34 | 375 A1 | |
| 159 BD49 | 431 BD16 | |
| 199 BD47 | ||
| 202 BD47 | ||
| 222 BD47 | ||
| 248 BD14 | ||
| 248 BD15 | ||
| 255 BD41 | ||
| 286 BD40 | ||
| 286 BD48 | ||
| 304 BD47 | ||
| 320 BD13 | ||
| 348 BD11 | ||
| 364 BD44 | ||
| 404 BD44 | ||
| 410 BD4 | ||
| 429 BD47 |
The BD modes are implemented at the end of the test and assume a fixed effectiveness factor equal to 0.6 (i.e., 40% of the failure intensity will remain after the fixes are implemented).
Solution
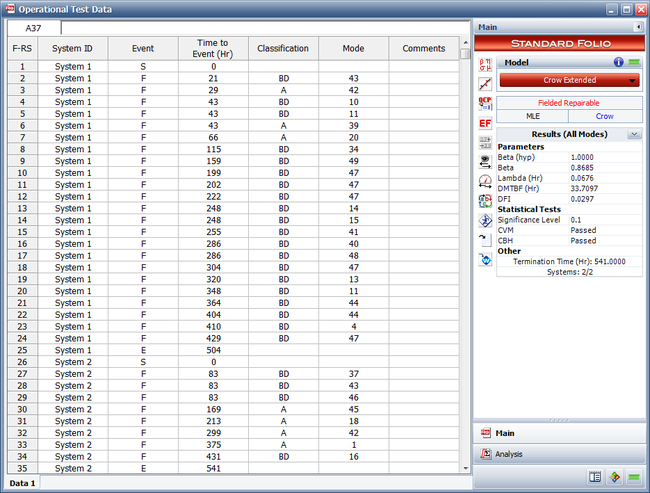
- The entered operational testing data and the estimated parameters are given below.
The assumption of [math]\displaystyle{ \beta = 1\,\! }[/math] can be verified by looking at the confidence bounds on [math]\displaystyle{ \beta\,\! }[/math] via the Quick Calculation Pad (QCP). The 90% 2-sided Crow confidence bounds on [math]\displaystyle{ \beta\,\! }[/math] are shown next.
Since the confidence bounds on [math]\displaystyle{ \beta\,\! }[/math] include one, then you can fail to reject the hypothesis that [math]\displaystyle{ \beta = 1\,\! }[/math].
- From #1, the demonstrated MTBF (DMTBF) equals 33.7097 Hr.
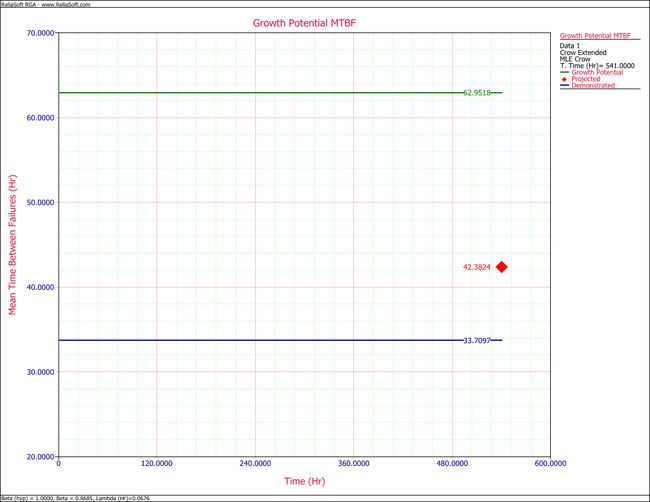
- The projected MTBF and growth potential values can be displayed via the Growth Potential MTBF plot.
From the plot the projected MTBF equals 42.3824 Hr. The growth potential MTBF equals 62.9518 Hr.