Crow Extended - Continuous Evaluation Model Examples

New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.

As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at RGA examples and RGA reference examples.

---

These examples appear in the Reliability Growth and Repairable System Analysis Reference book.

Parameter Estimation Example

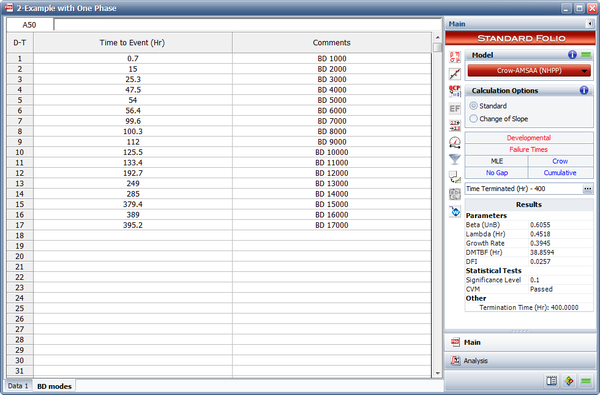
The following table shows a date set with failure and fix implementation events.

Multi-Phase Data for a Time Terminated Test at [math]\displaystyle{ T=400\,\! }[/math]
Event	Time to Event	Classification	Mode		Event	Time to Event	Classification	Mode
F	0.7	BD	1000		F	244.8	A	3
F	15	BD	2000		F	249	BD	13000
F	17.6	BC	200		F	250.8	A	2
F	25.3	BD	3000		F	260.1	BD	2000
F	47.5	BD	4000		F	273.1	A	5
I	50	BD	1000		F	274.7	BD	11000
F	54	BD	5000		I	280	BD	9000
F	54.5	BC	300		F	282.8	BC	902
F	56.4	BD	6000		F	285	BD	14000
F	63.6	A	1		F	315.4	BD	4000
F	72.2	BD	5000		F	317.1	A	3
F	99.2	BC	400		F	320.6	A	1
F	99.6	BD	7000		F	324.5	BD	12000
F	100.3	BD	8000		F	324.9	BD	10000
F	102.5	A	2		F	342	BD	5000
F	112	BD	9000		F	350.2	BD	3000
F	112.2	BC	500		F	355.2	BC	903
F	120.9	BD	2000		F	364.6	BD	10000
F	121.9	BC	600		F	364.9	A	1
F	125.5	BD	10000		I	365	BD	10000
F	133.4	BD	11000		F	366.3	BD	2000
F	151	BC	700		F	379.4	BD	15000
F	163	BC	800		F	389	BD	16000
F	174.5	BC	900		I	390	BD	15000
F	177.4	BD	10000		I	393	BD	16000
F	191.6	BC	901		F	394.9	A	3
F	192.7	BD	12000		F	395.2	BD	17000
F	213	A	1

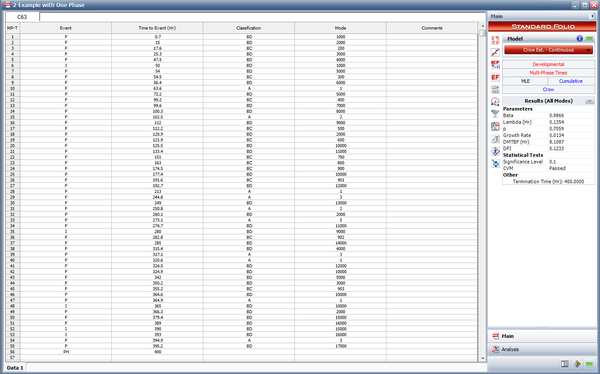
The following figure shows the data set entered in the RGA software's Multi-Phase data sheet. Note that because this is a time terminated test with a single phase ending at [math]\displaystyle{ T=400\,\! }[/math], the last event entry is a phase (PH) with time to event = 400.

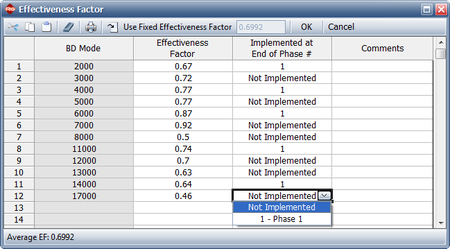
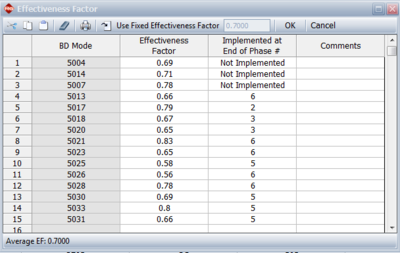
The next figure shows the effectiveness factors for the unfixed BD modes, and information concerning whether the fix will be implemented. Since we have only one test phase for this example, the notation "1" indicates that the fix will be implemented at the end of the first (and only) phase.

Do the following:

1. Determine the current demonstrated MTBF and failure intensity at time [math]\displaystyle{ T\,\! }[/math].
2. Determine the nominal and actual average effectiveness factor at time [math]\displaystyle{ T\,\! }[/math].
3. Determine the [math]\displaystyle{ p\,\! }[/math] ratio.
4. Determine the nominal and actual growth potential factor.
5. Determine the unfixed BD mode failure intensity at time [math]\displaystyle{ T.\,\! }[/math]
6. Determine the rate of discovery parameters and the rate of discovery function at time [math]\displaystyle{ T.\,\! }[/math]
7. Determine the nominal growth potential failure intensity and MTBF at time [math]\displaystyle{ T.\,\! }[/math]
8. Determine the nominal projected failure intensity and MTBF at time [math]\displaystyle{ T.\,\! }[/math]
9. Determine the actual growth potential failure intensity and MTBF at time [math]\displaystyle{ T.\,\! }[/math]
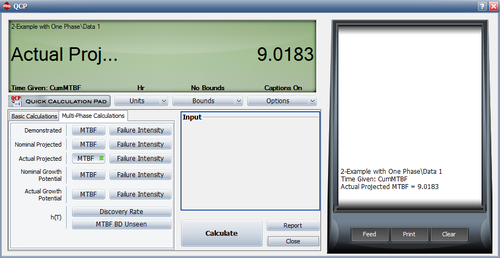
10. Determine the actual projected failure intensity and MTBF at time [math]\displaystyle{ T.\,\! }[/math]

Solution

1. As described in the Crow-AMSAA (NHPP) chapter, for a time terminated test, [math]\displaystyle{ \beta \,\! }[/math] is estimated by the following equation:

   [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}}\,\! }[/math]

   where [math]\displaystyle{ {{T}^{*}}\,\! }[/math] is the termination time and [math]\displaystyle{ n\,\! }[/math] is the total number of failures. In this example, [math]\displaystyle{ T^{*}=400\,\! }[/math] and [math]\displaystyle{ n=50\,\! }[/math]. Note that there are 5 fix implementation events and 1 event that marks the end of the phase. These should not be counted as failures. So in this case, we find that [math]\displaystyle{ \beta =0.9866.\,\! }[/math] We calculated the biased estimate of [math]\displaystyle{ \beta \,\! }[/math], but note that we could have used the unbiased estimate as presented in the Crow-AMSAA (NHPP) chapter. The choice of calculating the biased or unbiased estimate of [math]\displaystyle{ \beta \,\! }[/math] can be configured in the Application Setup window in the RGA software. Solve for [math]\displaystyle{ \lambda ,\,\! }[/math] based on the Crow-AMSAA (NHPP) equation explained in the Crow_AMSAA (NHPP) chapter:

   [math]\displaystyle{ \begin{align} \widehat{\lambda }= & \frac{n}{{{T}^{*\beta }}} \\ = & \frac{50}{{{400}^{0.9866}}} \\ = & 0.1354 \end{align}\,\! }[/math]

   The demonstrated MTBF of the system at time [math]\displaystyle{ T=400\,\! }[/math] is:

   [math]\displaystyle{ \begin{align} MTB{{F}_{D}}= & \frac{1}{\lambda \beta {{T}^{\beta -1}}} \\ = & 8.1087 \end{align}\,\! }[/math]

   The corresponding current demonstrated failure intensity is:

   [math]\displaystyle{ \begin{align} {{\lambda }_{D}}= & \frac{1}{MTB{{F}_{D}}} \\ = & 0.1233 \end{align}\,\! }[/math]

2. The average nominal effectiveness factor at time [math]\displaystyle{ T\,\! }[/math] is:

   [math]\displaystyle{ \begin{align} {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ = & \frac{0.67+0.72+0.77+0.77+0.87+0.92+0.5+0.74+0.7+0.63+0.64+0.46}{12} \\ = & 0.6992 \end{align}\,\! }[/math]

   The average actual effectiveness factor at time [math]\displaystyle{ T\,\! }[/math] is given by:

   [math]\displaystyle{ \begin{align} {{d}_{A}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ai}}}{M} \\ = & \frac{0.67+0+0.77+0+0.87+0+0+0.74+0+0+0.64+0}{12} \\ = & 0.3075 \end{align}\,\! }[/math]

3. The [math]\displaystyle{ p\,\! }[/math] ratio is calculated by:

   [math]\displaystyle{ \begin{align} p= & \frac{\text{Total number of distinct unfixed BD modes at time }400}{\text{Total number of distinct BD modes at time }400\text{ (both fixed and unfixed)}} \\ = & \frac{12}{12+5} \\ = & 0.7059 \end{align}\,\! }[/math]

4. The nominal growth potential factor is:

   [math]\displaystyle{ {{\lambda }_{NGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ni}} \right)\frac{{{N}_{i}}}{T}\,\! }[/math]

   The total number [math]\displaystyle{ M\,\! }[/math] of distinct unfixed BD modes at time 400 is [math]\displaystyle{ M=12.\,\! }[/math]

   [math]\displaystyle{ {{d}_{Ni}}\,\! }[/math] is the assigned (nominal) EF for the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] unfixed BD mode at time [math]\displaystyle{ {{T}_{j}},\,\! }[/math] (which is shown in the picture of the Effectiveness Factors window given above).

   [math]\displaystyle{ {{N}_{i}}\,\! }[/math] is the total number of failures over (0, 400) for the distinct unfixed BD mode [math]\displaystyle{ i\,\! }[/math]. This is summarized in the following table.

   Number of Failures for Unfixed BD Modes
   Classification	Mode	Number of Failures
   BD	2000	4
   BD	3000	2
   BD	4000	2
   BD	5000	3
   BD	6000	1
   BD	7000	1
   BD	8000	1
   BD	11000	2
   BD	12000	2
   BD	13000	1
   BD	14000	1
   BD	17000	1
   		Sum = 21

   Based on the information given above, the nominal growth potential factor is calculated as:

   [math]\displaystyle{ \begin{align} {{\lambda }_{NGPFactor}}=0.0153 \end{align}\,\! }[/math]

   The actual growth potential factor is:

   [math]\displaystyle{ {{\lambda }_{AGPFactor}}=\underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{Ai}} \right)\frac{{{N}_{i}}}{T}\,\! }[/math]

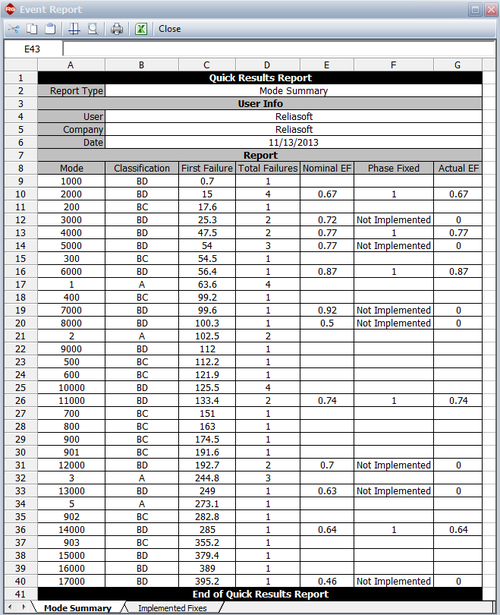
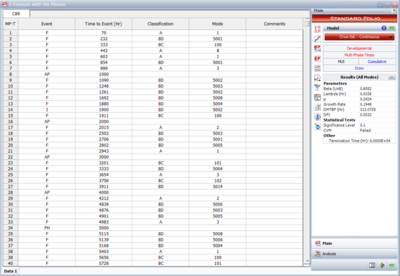
   where [math]\displaystyle{ {{d}_{Ai}}\,\! }[/math] is the actual EF for the [math]\displaystyle{ {{i}^{th}}\,\! }[/math] unfixed BD mode at time 400, depending on whether a fix was implemented at time 400 or not. The next figure shows an event report from the RGA software where the actual EF is zero if a fix was not implemented at 400, or equal to the nominal EF if the fix was implemented at 400.

   

   Based on the information given above, the actual growth potential factor is calculated as:

   [math]\displaystyle{ \begin{align} {{\lambda }_{AGPFactor}}=0.0344 \end{align}\,\! }[/math]

5. The total number of unfixed BD modes listed in the data table is 21. The unfixed BD mode failure intensity at time 400 is:

   [math]\displaystyle{ \begin{align} {{\lambda}_{BD unfixed}}= & \frac{\text{Total number of unfixed BD failure at time 400}}{400}\\ = & \frac{21}{400}\\ = & 0.0525 \end{align}\,\! }[/math]

6. The discovery rate parameters at time 400 are calculated by using all the first occurrences of all the BD modes, both fixed and unfixed. [math]\displaystyle{ {{\hat{\beta }}_{BD}}\,\! }[/math] is the unbiased estimated of [math]\displaystyle{ \beta \,\! }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes in our example. [math]\displaystyle{ {{\hat{\lambda }}_{BD}}\,\! }[/math] is the unbiased estimate of [math]\displaystyle{ \lambda \,\! }[/math] for the Crow-AMSAA (NHPP) model based on the first occurrence of the 17 distinct BD modes. The next figure shows the first time to failure for each of the 17 distinct modes and the results of the analysis using the Crow-AMSAA (NHPP) model in the RGA software (note that in this case, the calculation settings in the User Setup is configured to calculate the unbiased [math]\displaystyle{ \beta \,\! }[/math]).
   

   So we have:

   [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6055\,\! }[/math]

   and:

   [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.4518\,\! }[/math]

   The equations used to determine these parameters have been explained in question 1 of this example and are also presented in detail in the Crow-AMSA (NHPP) chapter.

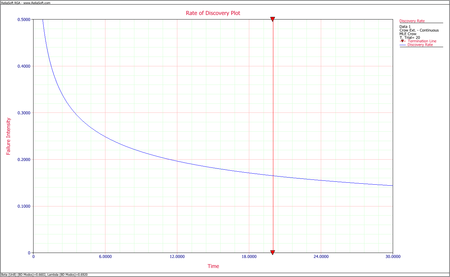
   The discovery rate function at time 400 is:

   [math]\displaystyle{ \begin{align} \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ = & 0.4518\cdot 0.6055\cdot {{400}^{0.6055-1}} \\ = & 0.0257 \end{align}\,\! }[/math]

   This is the failure intensity of the unseen BD modes at time 400. In this case, it means that 0.0257 new BD modes are discovered per hour, or one new BD mode is discovered every 38.9 hours.

7. The nominal growth potential failure intensity is:

   [math]\displaystyle{ \begin{align} {{\lambda}_{NGP}}= & {{\lambda}_{D}} - {{\lambda }_{BD unfixed}} + {{\lambda }_{NGP Factor}} + {{d}_{N}} \cdot p \cdot h (400) - {{d}_{N}}h (400) \\ = & 0.1233 - 0.0525 + 0.0153 + 0.6992 \cdot 0.7059 \cdot 0.0257 - 0.6992 \cdot 0.0257\\ = & 0.080 \end{align}\,\! }[/math]

   This is the minimum attainable failure intensity if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed. The nominal growth potential MTBF is:

   [math]\displaystyle{ \begin{align} MTB{{F}_{NGP}}= & \frac{1}{{{\lambda }_{NGP}}} \\ = & \frac{1}{0.080} \\ = & 12.37 \end{align}\,\! }[/math]

   This is the maximum attainable MTBF if all delayed corrective actions are implemented for the modes that have been seen and delayed corrective actions are also implemented for the unseen BD modes, assuming testing would continue until all unseen BD modes are revealed.
8. The nominal projected failure intensity at time [math]\displaystyle{ 400\,\! }[/math] is:

   [math]\displaystyle{ \begin{align} {{\lambda }_{NP}}= & {{\lambda }_{NGP}}+{{d}_{N}}h(400) \\ = & 0.080+0.6992\cdot 0.0257 \\ = & 0.0988 \end{align}\,\! }[/math]

   This is the projected failure intensity assuming all delayed fixes have been implemented for the modes that have been seen. The nominal projected MTBF at time 400 is:

   [math]\displaystyle{ \begin{align} MTB{{F}_{NP}}= & \frac{1}{{{\lambda }_{NP}}} \\ = & \frac{1}{0.0988} \\ = & 10.11 \end{align}\,\! }[/math]

   This is the projected MTBF assuming all delayed fixes have been implemented for the modes that have been seen.
9. The actual growth potential failure intensity is:

   [math]\displaystyle{ \begin{align} {{\lambda}_{AGP}}= & {{\lambda}_{D}} - {{\lambda }_{BD unfixed}} + {{\lambda }_{AGP Factor}} + {{d}_{A}} \cdot p \cdot h (400) - {{d}_{A}}h (400) \\ = & 0.1233 - 0.0525 + 0.0344 + 0.3075 \cdot 0.7059 \cdot 0.0257 - 0.3075 \cdot 0.0257\\ = & 0.1029 \end{align}\,\! }[/math]

   This is the minimum attainable failure intensity based on the current management strategy. The actual growth potential MTBF is:

   [math]\displaystyle{ \begin{align} MTB{{F}_{AGP}}= & \frac{1}{{{\lambda }_{AGP}}} \\ = & \frac{1}{0.1029} \\ = & 9.71 \end{align}\,\! }[/math]

   This is the maximum attainable MTBF based on the current management strategy.
10. The actual projected failure intensity at time 400 is:

    [math]\displaystyle{ \begin{align} {{\lambda }_{AP}}= & {{\lambda }_{AGP}}+{{d}_{A}}\cdot h\left( 400 \right) \\ = & 0.1029+0.3075\cdot 0.0257 \\ = & 0.1108 \end{align}\,\! }[/math]

    This is the projected failure intensity based on the current management strategy. The actual projected MTBF at time 400 is:

    [math]\displaystyle{ \begin{align} MTB{{F}_{AP}}= & \frac{1}{{{\lambda }_{AP}}} \\ = & \frac{1}{0.1108} \\ = & 9.01 \end{align}\,\! }[/math]

    This is the projected MTBF based on the current management strategy. The next figure demonstrates how we can derive the results of this example by using the software's Quick Calculation Pad (QCP). Here we chose to calculate the actual projected MTBF.
    

Multi-Phase Planning and Management

The Crow Extended - Continuous Evaluation model allows data analysis across multiple phases, up to seven individual phases. The next figure shows a portion of failure time test results obtained across six phases. Analysis points are specified for continuous evaluation every 1,000 hours. The cumulative test times at the end of each test phase are 5,000; 15,000; 25,000; 35,000; 45,000 and 60,000 hours.

The next figure shows the effectiveness factors for the BD modes that do not have an associated fix implementation event. In other words, these are unfixed BD modes. Note that this specifies the phase after which the BD mode will be fixed, if any.

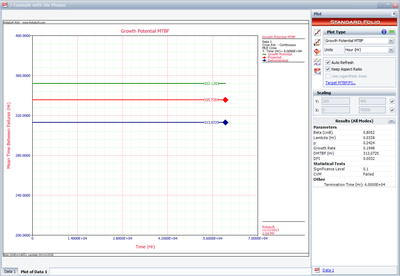
The next plot shows the overall test results in terms of demonstrated, projected and growth potential MTBF.

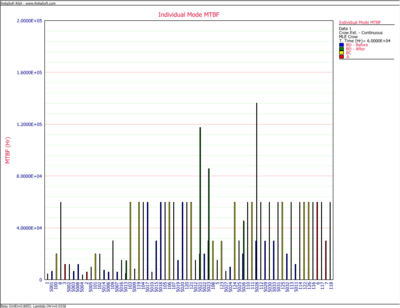
The next chart shows the "before" and "after" MTBFs for all the individual modes. Note that the "after" MTBFs are calculated by taking into account the respective effectiveness factors for each of the unfixed BD modes.

The analysis points are used to track overall growth inside and across phases, at desired intervals. The RGA software allows you to create a multi-phase plot that is associated with a multi-phase data sheet. In addition, if you have an existing growth planning folio in your RGA project, the multi-phase plot can plot the results from the multi-phase data sheet together with the reliability growth model from the growth planning folio. This allows you to track the overall reliability program against the goals, and set plans at each stage of the test. Additional information on combining a growth planning folio and a multi-phase plot is presented in the Reliability Growth Planning chapter.

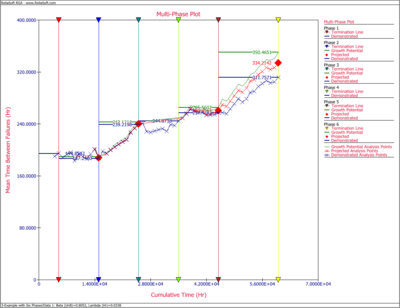
The next figure shows the multi-phase plot for the six phases of the reliability growth test program. This plot can be a powerful tool for overall tracking of the reliability growth program. It displays the termination time for each phase of testing, along with the demonstrated, projected and growth potential MTBFs at those times. The plot also displays the calculated MTBFs at specified analysis points, which are determined based on the "AP" events in the data sheet.

Multi-Phase Mixed Data Example

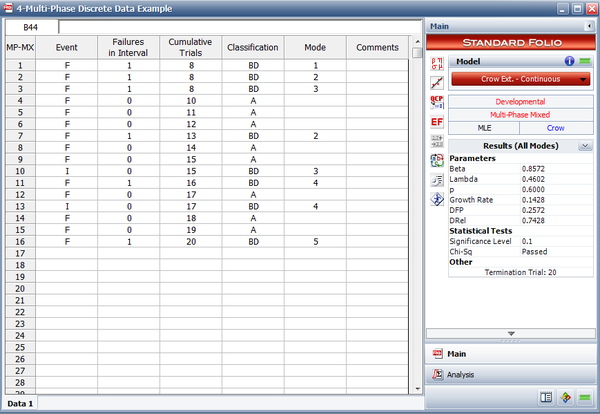
A one-shot system underwent reliability growth development for a total of 20 trials. The test was performed as a combination of configuration in groups and individual trial-by-trial. The following table shows the obtained data set. The Failures in Interval column specifies the number of failures that occurred in each interval, and the Cumulative Trials column specifies the cumulative number of trials at the end of that interval.

Mixed Data
Event	Failures in Interval	Cumulative Trials	Classification	Mode
F	1	8	BD	1
F	1	8	BD	2
F	1	8	BD	3
F	0	10	A
F	0	11	A
F	0	12	A
F	1	13	BD	2
F	0	14	A
F	0	15	A
I	0	15	BD	3
F	1	16	BD	4
F	0	17	A
I	0	17	BD	4
F	0	18	A
F	0	18	A
F	1	20	BD	5

The table also gives the classifications of the failure modes. There are 5 BD modes. Of these 5 modes, 2 are corrected during the test (BD3 and BD4) and 3 have not been corrected by time [math]\displaystyle{ T=20\,\! }[/math] (BD1, BD2 and BD5). Do the following:

1. Calculate the parameters of the Crow Extended - Continuous Evaluation model.
2. Calculated the demonstrated reliability at the end of the test.
3. Calculate parameter [math]\displaystyle{ p\,\! }[/math].
4. Calculate the unfixed BD mode failure probability.
5. Calculate the nominal growth potential factor.
6. Calculate the nominal average effectiveness factor.
7. Calculate the discovery failure intensity function at the end of the test.
8. Calculate the nominal projected reliability at the end of the test.
9. Calculate the nominal growth potential reliability at the end of the test.

Solution

1. The next figure shows the data entered in the RGA software.
   

   The parameters [math]\displaystyle{ \beta \,\! }[/math] and [math]\displaystyle{ \lambda \,\! }[/math] are calculated as follows (the calculations for these parameters are presented in detail in the Crow-AMSAA (NHPP) chapter):

   [math]\displaystyle{ \widehat{\beta }=0.8572\,\! }[/math]

   and:

   [math]\displaystyle{ \widehat{\lambda }=0.4602\,\! }[/math]

2. The corresponding demonstrated unreliability is calculated as:

   [math]\displaystyle{ \begin{align} {{f}_{D}}=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 \end{align}\,\! }[/math]

   Using the parameter estimates given above, the instantaneous unreliability at the end of the test (or [math]\displaystyle{ T=20\,\! }[/math]) is equal to:

   [math]\displaystyle{ {{f}_{D}}(20)=0.8572\cdot 0.4602\cdot {{20}^{0.8572-1}}=0.2572\,\! }[/math]

   The demonstrated reliability is:

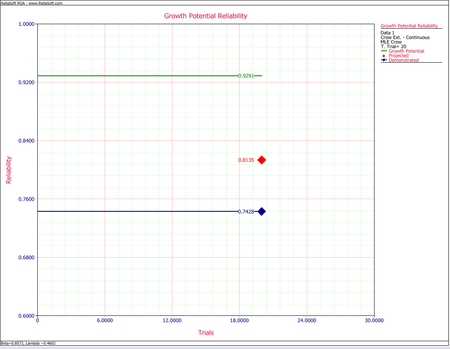
   [math]\displaystyle{ \begin{align} {{R}_{D}}= & 1-{{f}_{D}} \\ = & 1-0.2572=0.7428 \end{align}\,\! }[/math]

   Note that in discrete data, we calculate the reliability and not MTBF because we are dealing with the number of trials and not test time.
3. Assume that the following effectiveness factors are assigned to the unfixed BD modes:

   Classification	Mode	Effectiveness Factor	Implemented at End of Phase
   BD	1	0.65	Phase 1
   BD	2	0.70	Phase 1
   BD	5	0.75	Phase 1

   The parameter [math]\displaystyle{ p\,\! }[/math] is the total number of distinct unfixed BD modes at time [math]\displaystyle{ T\,\! }[/math] divided by the total number of distinct BD (fixed and unfixed) modes.

   In this example:

   [math]\displaystyle{ p=\frac{3}{5}=0.6\,\! }[/math]

4. The unfixed BD mode failure probability at time [math]\displaystyle{ T\,\! }[/math] is the total number of unfixed BD failures (classified at time [math]\displaystyle{ T\,\! }[/math] ) divided by the total trials. Based on the table at the beginning of the example, we have:

   [math]\displaystyle{ {{f}_{BD, unfixed}}=\frac{4}{20}=0.2\,\! }[/math]

5. The nominal growth potential factor is:

   [math]\displaystyle{ \begin{align} {{\lambda }_{NGPFactor}}= & \underset{i=1}{\overset{M}{\mathop \sum }}\,\left( 1-{{d}_{i}} \right)\frac{{{N}_{i}}}{T} \\ = & \left( 1-{{d}_{1}} \right)\frac{{{N}_{1}}}{T}+\left( 1-{{d}_{2}} \right)\frac{{{N}_{2}}}{T}+\left( 1-{{d}_{5}} \right)\frac{{{N}_{5}}}{T} \\ = & \left( 1-0.65 \right)\frac{1}{20}+\left( 1-0.70 \right)\frac{2}{20}+\left( 1-0.75 \right)\frac{1}{20} \\ = & 0.06 \end{align}\,\! }[/math]

6. The nominal average effectiveness factor is:

   [math]\displaystyle{ \begin{align} {{d}_{N}}= & \frac{\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{d}_{Ni}}}{M} \\ = & \frac{0.65+0.70+0.75}{3} \\ = & 0.70 \end{align}\,\! }[/math]

7. The discovery function at time [math]\displaystyle{ T\,\! }[/math] is calculated using all the first occurrences of all the BD modes, both fixed and unfixed. In our example, we calculate [math]\displaystyle{ {{\widehat{\beta }}_{BD}}\,\! }[/math] and [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}\,\! }[/math] using only the unfixed BD modes and excluding the second occurrence of BD2, which results in the following:

   [math]\displaystyle{ {{\widehat{\beta }}_{BD}}=0.6602\,\! }[/math]

   and:

   [math]\displaystyle{ {{\widehat{\lambda }}_{BD}}=0.6920\,\! }[/math]

   So the discovery failure intensity function at time [math]\displaystyle{ T=20\,\! }[/math] is:

   [math]\displaystyle{ \begin{align} \widehat{h}(T|BD)= & {{\widehat{\lambda }}_{BD}}{{\widehat{\beta }}_{BD}}{{T}^{{{\widehat{\beta }}_{BD}}-1}} \\ = & 0.6920\cdot 0.6602\cdot {{20}^{0.6602-1}} \\ = & 0.16507 \end{align}\,\! }[/math]

   The next figure shows the plot for the discovery failure intensity function.
   
8. The nominal projected failure probability at time [math]\displaystyle{ T=20\,\! }[/math] is:

   [math]\displaystyle{ \begin{align} {{f}_{NP}}= & {{f}_{NGP}}+{{d}_{N}}h(T) \\ = & 0.0701+0.7\cdot 0.16507 \\ = & 0.1865 \end{align}\,\! }[/math]

   Therefore, the nominal projected reliability is:

   [math]\displaystyle{ \begin{align} {{R}_{P}}= & 1-0.1856= \\ = & 0.8135 \end{align}\,\! }[/math]

9. The nominal growth potential unreliability is:

   [math]\displaystyle{ {{f}_{NGP}} = {{f}_{D}} - {{f}_{BD unfixed}} + {{\lambda}_{NGPFactor}} + {{d}_{N}}\cdot p \cdot h(T) - {{d}_{N}}h(T)\,\! }[/math]

   Based on the previous calculation for this example, we have:

   [math]\displaystyle{ \begin{align} {{f}_{NGP}}= & 0.2572-0.2+0.06+0.7\cdot 0.6\cdot 0.16507-0.7\cdot 0.16507 \\ = & 0.0709 \end{align}\,\! }[/math]

   So the nominal growth potential reliability is:

   [math]\displaystyle{ \begin{align} {{R}_{NGP}}= & 1-0.0709 \\ = & 0.9291 \end{align}\,\! }[/math]

   The next figure shows the plot for the instantaneous demonstrated, projected and growth potential reliability.