Eyring Example: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding: | The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding: | ||
::<math>\widehat{\beta }=4.29186497\,\!</math> | |||
::<math>\widehat{ | ::<math>\widehat{A}=-11.08784624\,\!</math> | ||
::<math>\widehat{B}=1454.08635742\,\!</math> | |||
::<math>\widehat{B}=1454.08635742</math> | |||
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using: | Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using: | ||
::<math>\overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\!</math> | |||
::<math>\overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)</math> | |||
or: | or: | ||
| Line 26: | Line 24: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
& \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr | & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr | ||
\end{align}</math> | \end{align}\,\!</math> | ||
Revision as of 22:13, 21 September 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at ALTA examples and ALTA reference examples.
This example appears in the Accelerated Life Testing Data Analysis Reference book.
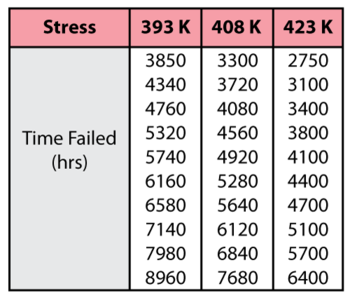
Consider the following times-to-failure data at three different stress levels.
The data set was entered into the ALTA standard folio and analyzed using the Eyring-Weibull model, yielding:
- [math]\displaystyle{ \widehat{\beta }=4.29186497\,\! }[/math]
- [math]\displaystyle{ \widehat{A}=-11.08784624\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1454.08635742\,\! }[/math]
Once the parameters of the model are defined, other life measures can be directly obtained using the appropriate equations. For example, the MTTF can be obtained for the use stress level of 323 K by using:
- [math]\displaystyle{ \overline{T}=\frac{1}{V}{{e}^{-\left( A-\tfrac{B}{V} \right)}}\cdot \Gamma \left( \frac{1}{\beta }+1 \right)\,\! }[/math]
or:
- [math]\displaystyle{ \begin{align} & \overline{T}= & \frac{1}{323}{{e}^{-\left( -11.08784624-\tfrac{1454.08635742}{323} \right)}}\cdot \Gamma \left( \frac{1}{4.29186497}+1 \right) =16,610\text{ }hr \end{align}\,\! }[/math]