Crow-AMSAA (NHPP): Difference between revisions
Lisa Hacker (talk | contribs) |
Lisa Hacker (talk | contribs) |
||
| Line 892: | Line 892: | ||
The process to calculate the average unreliability confidence bounds for mixed data is as follows: | The process to calculate the average unreliability confidence bounds for mixed data is as follows: | ||
<br> | <br> | ||
:1) Calculate the average failure probability | :1) Calculate the average failure probability <math>({{t}_{1}},{{t}_{2}})\,\!</math>. | ||
:2) There will exist a <math>{{t}^{*}}\,\!</math> between <math>{{t}_{1}}\,\!</math> and <math>{{t}_{2}}\,\!</math> such that the instantaneous unreliability at <math>{{t}^{*}}\,\!</math> equals the average unreliability <math>({{t}_{1}},{{t}_{2}})\,\!</math> | :2) There will exist a <math>{{t}^{*}}\,\!</math> between <math>{{t}_{1}}\,\!</math> and <math>{{t}_{2}}\,\!</math> such that the instantaneous unreliability at <math>{{t}^{*}}\,\!</math> equals the average unreliability <math>({{t}_{1}},{{t}_{2}})\,\!</math>. The confidence intervals for the instantaneous unreliability at <math>{{t}^{*}}\,\!</math> are the confidence intervals for the average unreliability <math>({{t}_{1}},{{t}_{2}})\,\!</math>. | ||
<br> | <br> | ||
'''Bounds on Average Reliability for Mixed Data'''<br> | '''Bounds on Average Reliability for Mixed Data'''<br> | ||
The process to calculate the average reliability confidence bounds for mixed data is as follows: | The process to calculate the average reliability confidence bounds for mixed data is as follows: | ||
<br> | <br> | ||
:1) Calculate confidence bounds for average unreliability | :1) Calculate confidence bounds for average unreliability <math>({{t}_{1}},{{t}_{2}})\,\!</math> as described above. | ||
:2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability. | :2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability. | ||
Revision as of 01:01, 24 August 2012
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
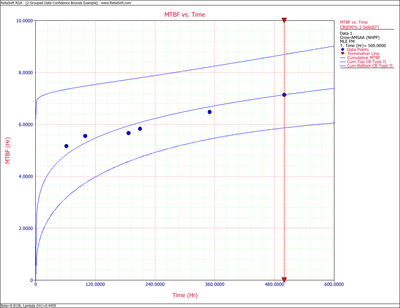
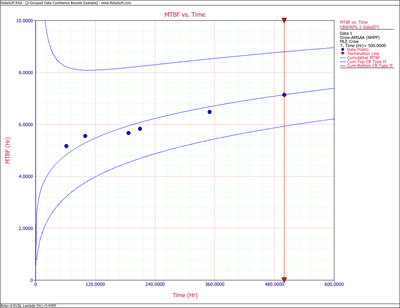
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
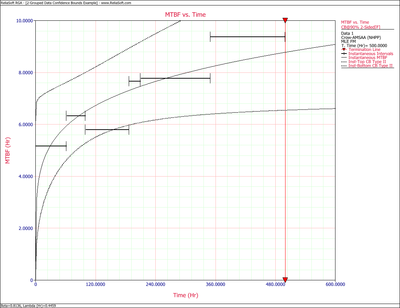
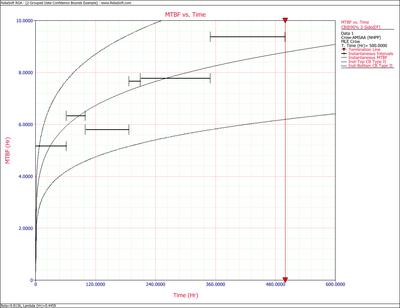
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
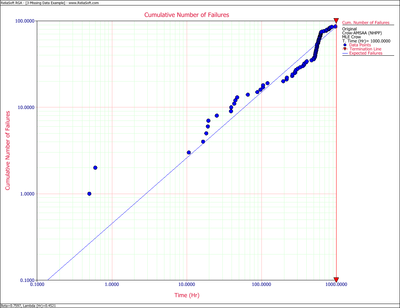
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
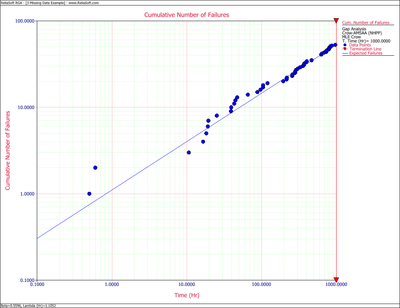
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
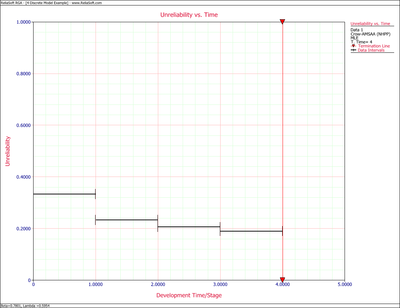
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
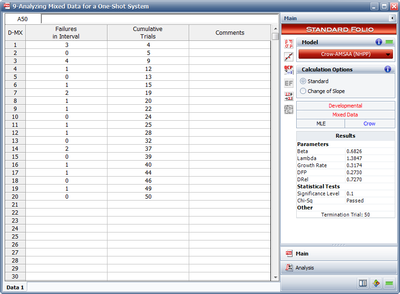
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
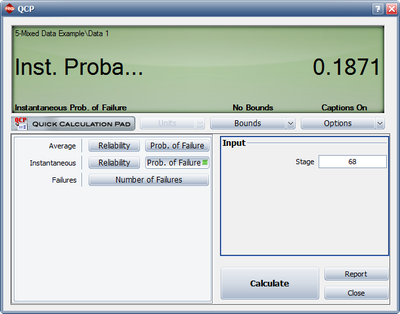
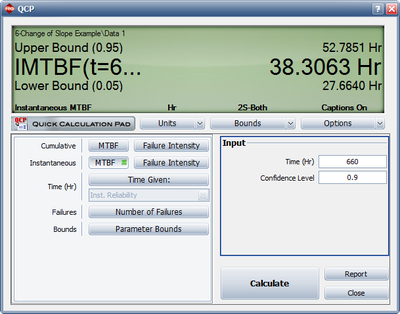
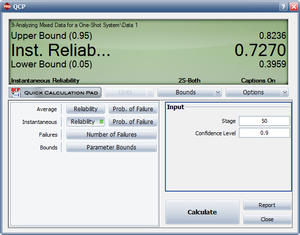
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
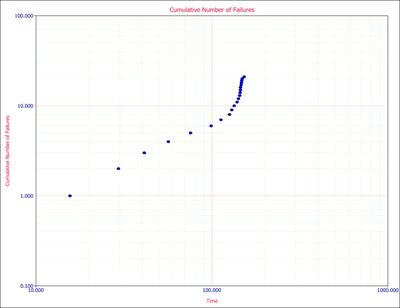
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
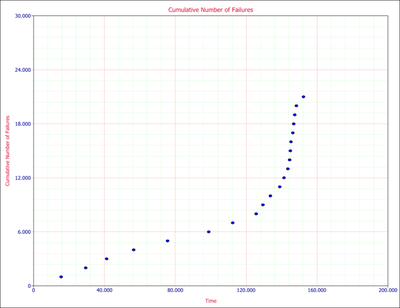
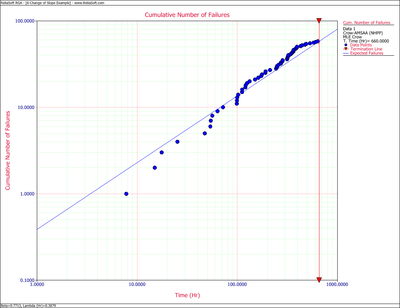
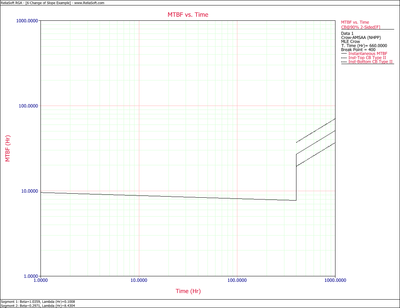
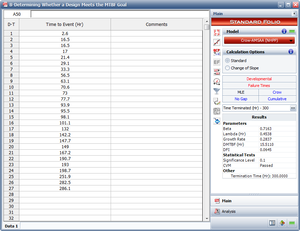
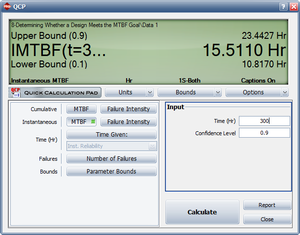
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
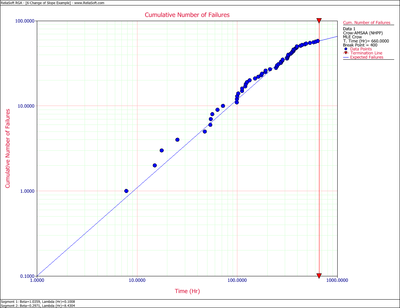
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
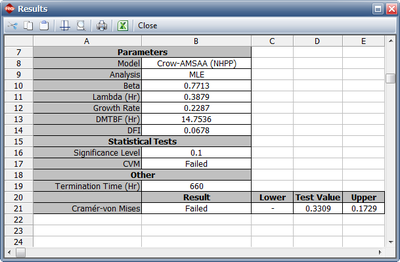
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
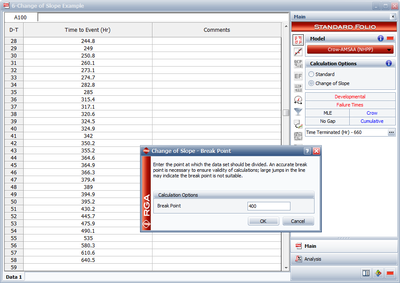
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
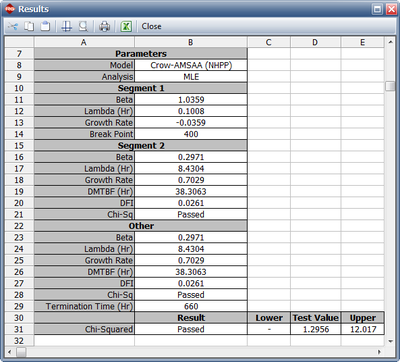
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
In "Reliability Analysis for Complex, Repairable Systems" (1974), Dr. Larry H. Crow noted that the Duane model could be stochastically represented as a Weibull process, allowing for statistical procedures to be used in the application of this model in reliability growth. This statistical extension became what is known as the Crow-AMSAA (NHPP) model. This method was first developed at the U.S. Army Materiel Systems Analysis Activity (AMSAA). It is frequently used on systems when usage is measured on a continuous scale. It can also be applied for the analysis of one shot items when there is high reliability and large number of trials.
Test programs are generally conducted on a phase by phase basis. The Crow-AMSAA model is designed for tracking the reliability within a test phase and not across test phases. A development testing program may consist of several separate test phases. If corrective actions are introduced during a particular test phase then this type of testing and the associated data are appropriate for analysis by the Crow-AMSAA model. The model analyzes the reliability growth progress within each test phase and can aid in determining the following:
- Reliability of the configuration currently on test
- Reliability of the configuration on test at the end of the test phase
- Expected reliability if the test time for the phase is extended
- Growth rate
- Confidence intervals
- Applicable goodness-of-fit tests
Crow-AMSAA (NHPP) Model
The reliability growth pattern for the Crow-AMSAA model is exactly the same pattern as for the Duane postulate discussed previously. That is, the cumulative number of failures is linear when plotted on ln-ln scale. Unlike the Duane postulate, the Crow-AMSAA model is statistically based. Under the Duane postulate, the failure rate is linear on ln-ln scale. However for the Crow-AMSAA model statistical structure, the failure intensity of the underlying non-homogeneous Poisson process (NHPP) is linear when plotted on ln-ln scale.
Let [math]\displaystyle{ N(t) }[/math] be the cumulative number of failures observed in cumulative test time [math]\displaystyle{ t }[/math] and let [math]\displaystyle{ \rho (t) }[/math] be the failure intensity for the Crow-AMSAA model. Under the NHPP model, [math]\displaystyle{ \rho (t)\Delta t }[/math] is approximately the probably of a failure occurring over the interval [math]\displaystyle{ [t,t+\Delta t] }[/math] for small [math]\displaystyle{ \Delta t }[/math] . In addition, the expected number of failures experienced over the test interval [math]\displaystyle{ [0,T] }[/math] under the Crow-AMSAA model is given by:
- [math]\displaystyle{ E[N(T)]=\mathop{}_{0}^{T}\rho (t)dt }[/math]
The Crow-AMSAA model assumes that [math]\displaystyle{ \rho (T) }[/math] may be approximated by the Weibull failure rate function:
- [math]\displaystyle{ \rho (T)=\frac{\beta }{{{\eta }^{\beta }}}{{T}^{\beta -1}} }[/math]
Therefore, if [math]\displaystyle{ \lambda =\tfrac{1}{{{\eta }^{\beta }}}, }[/math] the intensity function, [math]\displaystyle{ \rho (T), }[/math] or the instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
In the special case of exponential failure times there is no growth and the failure intensity, [math]\displaystyle{ \rho (t) }[/math] , is equal to [math]\displaystyle{ \lambda }[/math] . In this case, the expected number of failures is given by:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda T \end{align} }[/math]
In order for the plot to be linear when plotted on ln-ln scale under the general reliability growth case, the following must hold true where the expected number of failures is equal to:
- [math]\displaystyle{ \begin{align} & E[N(T)]= & \mathop{}_{0}^{T}\rho (t)dt \\ & = & \lambda {{T}^{\beta }} \end{align} }[/math]
To put a statistical structure on the reliability growth process, consider again the special case of no growth. In this case the number of failures, [math]\displaystyle{ N(T), }[/math] experienced during the testing over [math]\displaystyle{ [0,T] }[/math] is random. The expected number of failures, [math]\displaystyle{ N(T), }[/math] is said to follow the homogeneous (constant) Poisson process with mean [math]\displaystyle{ \lambda T }[/math] and is given by:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda T)}^{n}}{{e}^{-\lambda T}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
The Crow-AMSAA generalizes this no growth case to allow for reliability growth due to corrective actions. This generalization keeps the Poisson distribution for the number of failures but allows for the expected number of failures, [math]\displaystyle{ E[N(T)], }[/math] to be linear when plotted on ln-ln scale. The Crow-AMSAA model lets [math]\displaystyle{ E[N(T)]=\lambda {{T}^{\beta }} }[/math] . The probability that the number of failures, [math]\displaystyle{ N(T), }[/math] will be equal to [math]\displaystyle{ n }[/math] under growth is then given by the Poisson distribution:
- [math]\displaystyle{ \underset{}{\overset{}{\mathop{\Pr }}}\,[N(T)=n]=\frac{{{(\lambda {{T}^{\beta }})}^{n}}{{e}^{-\lambda {{T}^{\beta }}}}}{n!};\text{ }n=0,1,2,\ldots }[/math]
This is the general growth situation and the number of failures, [math]\displaystyle{ N(T) }[/math] , follows a non-homogeneous Poisson process. The exponential, "no growth" homogeneous Poisson process is a special case of the non-homogeneous Crow-AMSAA model. This is reflected in the Crow-AMSAA model parameter where [math]\displaystyle{ \beta =1 }[/math] . The cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{c}}=\lambda {{T}^{\beta -1}} }[/math]
The cumulative [math]\displaystyle{ MTB{{F}_{c}} }[/math] is:
- [math]\displaystyle{ MTB{{F}_{c}}=\frac{1}{\lambda }{{T}^{1-\beta }} }[/math]
As mentioned above, the local pattern for reliability growth within a test phase is the same as the growth pattern observed by Duane, discussed in the previous chapter. The Duane [math]\displaystyle{ MTB{{F}_{c}} }[/math] is equal to:
- [math]\displaystyle{ MTB{{F}_{{{c}_{DUANE}}}}=b{{T}^{\alpha }} }[/math]
And the Duane cumulative failure rate, [math]\displaystyle{ {{\lambda }_{c}} }[/math] , is:
- [math]\displaystyle{ {{\lambda }_{{{c}_{DUANE}}}}=\frac{1}{b}{{T}^{-\alpha }} }[/math]
Thus a relationship between Crow-AMSAA parameters and Duane parameters can be developed, such that:
- [math]\displaystyle{ \begin{align} & {{b}_{DUANE}}= & \frac{1}{{{\lambda }_{AMSAA}}} \\ & {{\alpha }_{DUANE}}= & 1-{{\beta }_{AMSAA}} \end{align} }[/math]
Note that these relationships are not absolute. They change according to how the parameters (slopes, intercepts, etc.) are defined when the analysis of the data is performed. For the exponential case, [math]\displaystyle{ \beta =1 }[/math] , then [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda }[/math] , a constant. For [math]\displaystyle{ \beta \gt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is increasing. This indicates a deterioration in system reliability. For [math]\displaystyle{ \beta \lt 1 }[/math] , [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] is decreasing. This is indicative of reliability growth. Note that the model assumes a Poisson process with Weibull intensity function, not the Weibull distribution. Therefore, statistical procedures for the Weibull distribution do not apply for this model. The parameter [math]\displaystyle{ \lambda }[/math] is called a scale parameter because it depends upon the unit of measurement chosen for [math]\displaystyle{ T }[/math] . [math]\displaystyle{ \beta }[/math] is the shape parameter that characterizes the shape of the graph of the intensity function.
The total number of failures, [math]\displaystyle{ N(T) }[/math] , is a random variable with Poisson distribution. Therefore, the probability that exactly [math]\displaystyle{ n }[/math] failures occur by time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ P[N(T)=n]=\frac{{{[\theta (T)]}^{n}}{{e}^{-\theta (T)}}}{n!} }[/math]
The number of failures occurring in the interval from [math]\displaystyle{ {{T}_{1}} }[/math] to [math]\displaystyle{ {{T}_{2}} }[/math] is a random variable having a Poisson distribution with mean:
- [math]\displaystyle{ \theta ({{T}_{2}})-\theta ({{T}_{1}})=\lambda (T_{2}^{\beta }-T_{1}^{\beta }) }[/math]
The number of failures in any interval is statistically independent of the number of failures in any interval that does not overlap the first interval. At time [math]\displaystyle{ {{T}_{0}} }[/math] , the failure intensity is [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . If improvements are not made to the system after time [math]\displaystyle{ {{T}_{0}} }[/math] , it is assumed that failures would continue to occur at the constant rate [math]\displaystyle{ {{\lambda }_{i}}({{T}_{0}})=\lambda \beta T_{0}^{\beta -1} }[/math] . Future failures would then follow an exponential distribution with mean [math]\displaystyle{ m({{T}_{0}})=\tfrac{1}{\lambda \beta T_{0}^{\beta -1}} }[/math] . The instantaneous [math]\displaystyle{ MTBF }[/math] of the system at time [math]\displaystyle{ T }[/math] is:
- [math]\displaystyle{ m(T)=\frac{1}{\lambda \beta {{T}^{\beta -1}}} }[/math]
Applicability
The Duane and Crow-AMSAA models are the most frequently used reliability growth models. Their relationship comes from the fact that both make use of the underlying observed linear relationship between the logarithm of cumulative MTBF and cumulative test time. However, the Duane model does not provide a capability to test whether the change in MTBF observed over time is significantly different from what might be seen due to random error between phases. The Crow-AMSAA model allows for such assessments. Also, the Crow-AMSAA allows for development of hypothesis testing procedures to determine growth presence in the data where ( [math]\displaystyle{ \beta \lt 1 }[/math] indicates that there is growth in MTBF, [math]\displaystyle{ \beta =1 }[/math] indicates a constant MTBF and [math]\displaystyle{ \beta \gt 1 }[/math] indicates a decreasing MTBF). Additionally, the Crow-AMSAA model views the process of reliability growth as probabilistic, while the Duane model views the process as deterministic.
Parameter Estimation
Maximum Likelihood Estimators
The probability density function ( [math]\displaystyle{ pdf }[/math] ) of the [math]\displaystyle{ {{i}^{th}} }[/math] event given that the [math]\displaystyle{ {{(i-1)}^{th}} }[/math] event occurred at [math]\displaystyle{ {{T}_{i-1}} }[/math] is:
- [math]\displaystyle{ f({{T}_{i}}|{{T}_{i-1}})=\frac{\beta }{\eta }{{\left( \frac{{{T}_{i}}}{\eta } \right)}^{\beta -1}}\cdot {{e}^{-\tfrac{1}{{{\eta }^{\beta }}}\left( T_{i}^{\beta }-T_{i-1}^{\beta } \right)}} }[/math]
The likelihood function is:
- [math]\displaystyle{ L={{\lambda }^{n}}{{\beta }^{n}}{{e}^{-\lambda {{T}^{*\beta }}}}\underset{i=1}{\overset{n}{\mathop \prod }}\,T_{i}^{\beta -1} }[/math]
where [math]\displaystyle{ {{T}^{*}} }[/math] is the termination time and is given by:
- [math]\displaystyle{ {{T}^{*}}=\left\{ \begin{matrix} {{T}_{n}}\text{ if the test is failure terminated} \\ T\gt {{T}_{n}}\text{ if the test is time terminated} \\ \end{matrix} \right\} }[/math]
Taking the natural log on both sides:
- [math]\displaystyle{ \Lambda =n\ln \lambda +n\ln \beta -\lambda {{T}^{*\beta }}+(\beta -1)\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
And differentiating with respect to [math]\displaystyle{ \lambda }[/math] yields:
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \lambda }=\frac{n}{\lambda }-{{T}^{*\beta }} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \lambda }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{{{T}^{*\beta }}} }[/math]
Now differentiate with respect to [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \frac{\partial \Lambda }{\partial \beta }=\frac{n}{\beta }-\lambda {{T}^{*\beta }}\ln {{T}^{*}}+\underset{i=1}{\overset{n}{\mathop \sum }}\,\ln {{T}_{i}} }[/math]
Set equal to zero and solve for [math]\displaystyle{ \beta }[/math] :
- [math]\displaystyle{ \widehat{\beta }=\frac{n}{n\ln {{T}^{*}}-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
Biasing and Unbiasing of Beta
The equation above returns the biased estimate of [math]\displaystyle{ \beta }[/math]. The unbiased estimate of [math]\displaystyle{ \beta }[/math] can be calculated by using the following relationships. For time terminated data (meaning that the test ends after a specified number of failures):
- [math]\displaystyle{ \bar{\beta }=\frac{N-1}{N}\hat{\beta } }[/math]
For failure terminated data (meaning that the test ends after a specified test time):
- [math]\displaystyle{ \bar{\beta }=\frac{N-2}{N}\hat{\beta } }[/math]
Crow-AMSAA Model Example
Two prototypes of a system were tested simultaneously with design changes incorporated during the test. The following table presents the data collected over the entire test. Find the Crow-AMSAA parameters and the intensity function using maximum likelihood estimators.
| Failure Number | Failed Unit | Test Time Unit 1(hr) | Test Time Unit 2(hr) | Total Test Time(hr) | [math]\displaystyle{ ln{(T)} }[/math] |
|---|---|---|---|---|---|
| 1 | 1 | 1.0 | 1.7 | 2.7 | 0.99325 |
| 2 | 1 | 7.3 | 3.0 | 10.3 | 2.33214 |
| 3 | 2 | 8.7 | 3.8 | 12.5 | 2.52573 |
| 4 | 2 | 23.3 | 7.3 | 30.6 | 3.42100 |
| 5 | 2 | 46.4 | 10.6 | 57.0 | 4.04305 |
| 6 | 1 | 50.1 | 11.2 | 61.3 | 4.11578 |
| 7 | 1 | 57.8 | 22.2 | 80.0 | 4.38203 |
| 8 | 2 | 82.1 | 27.4 | 109.5 | 4.69592 |
| 9 | 2 | 86.6 | 38.4 | 125.0 | 4.82831 |
| 10 | 1 | 87.0 | 41.6 | 128.6 | 4.85671 |
| 11 | 2 | 98.7 | 45.1 | 143.8 | 4.96842 |
| 12 | 1 | 102.2 | 65.7 | 167.9 | 5.12337 |
| 13 | 1 | 139.2 | 90.0 | 229.2 | 5.43459 |
| 14 | 1 | 166.6 | 130.1 | 296.7 | 5.69272 |
| 15 | 2 | 180.8 | 139.8 | 320.6 | 5.77019 |
| 16 | 1 | 181.3 | 146.9 | 328.2 | 5.79362 |
| 17 | 2 | 207.9 | 158.3 | 366.2 | 5.90318 |
| 18 | 2 | 209.8 | 186.9 | 396.7 | 5.98318 |
| 19 | 2 | 226.9 | 194.2 | 421.1 | 6.04287 |
| 20 | 1 | 232.2 | 206.0 | 438.2 | 6.08268 |
| 21 | 2 | 267.5 | 233.7 | 501.2 | 6.21701 |
| 22 | 2 | 330.1 | 289.9 | 620.0 | 6.42972 |
Solution
For the failure terminated test, [math]\displaystyle{ {\beta} }[/math] is:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-\underset{i=1}{\overset{22}{\mathop{\sum }}}\,\ln {{T}_{i}}} }[/math]
- where:
- [math]\displaystyle{ \underset{i=1}{\overset{22}{\mathop \sum }}\,\ln {{T}_{i}}=105.6355 }[/math]
- Then:
- [math]\displaystyle{ \widehat{\beta }=\frac{22}{22\ln 620-105.6355}=0.6142 }[/math]
And for [math]\displaystyle{ {\lambda} }[/math] :
- [math]\displaystyle{ \widehat{\lambda }=\frac{22}{{{620}^{0.6142}}}=0.4239 }[/math]
Therefore, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] becomes:
- [math]\displaystyle{ \begin{align} & {{\widehat{\lambda }}_{i}}(T)= & 0.4239\cdot 0.6142\cdot {{620}^{-0.3858}} \\ & = & 0.0217906\frac{\text{failures}}{\text{hr}} \end{align} }[/math]
The next figure shows the plot of the failure rate. If no further changes are made, the estimated MTBF is [math]\displaystyle{ \tfrac{1}{0.0217906} }[/math] or 46 hr.
Confidence Bounds
This section presents the methods used in the RGA software to estimate the confidence bounds for the Crow-AMSAA model when applied to developmental testing data. RGA provides two methods to estimate the confidence bounds. The Fisher Matrix (FM) method, which is commonly employed in the reliability field, is based on the Fisher information matrix. The Crow Bounds (Crow) method has been developed by Dr. Crow. Template loop detected: Template:Bounds on beta camsaa-cb
Template loop detected: Template:Bounds on lambda camsaa-cb
Template loop detected: Template:Bounds on growth rate camsaa-cb
Template loop detected: Template:Bounds on cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-cb
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-cb
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-cb
Template loop detected: Template:Bounds on cumulative number of failures camsaa-cb
Grouped Data
For analyzing grouped data, we follow the same logic described previously for the Duane model. If the [math]\displaystyle{ E[N(T)] }[/math] equation from the Crow-AMSAA (NHPP) Model section above is linearized:
- [math]\displaystyle{ \ln [E(N(T))]=\ln \lambda +\beta \ln T }[/math]
According to Crow [9], the likelihood function for the grouped data case, (where [math]\displaystyle{ {{n}_{1}}, }[/math] [math]\displaystyle{ {{n}_{2}}, }[/math] [math]\displaystyle{ {{n}_{3}},\ldots , }[/math] [math]\displaystyle{ {{n}_{k}} }[/math] failures are observed and [math]\displaystyle{ k }[/math] is the number of groups), is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\underset{}{\overset{}{\mathop{\Pr }}}\,({{N}_{i}}={{n}_{i}})=\underset{i=1}{\overset{k}{\mathop \prod }}\,\frac{{{(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}^{{{n}_{i}}}}\cdot {{e}^{-(\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })}}}{{{n}_{i}}!} }[/math]
And the MLE of [math]\displaystyle{ \lambda }[/math] based on this relationship is:
- [math]\displaystyle{ \widehat{\lambda }=\frac{n}{T_{k}^{\widehat{\beta }}} }[/math]
And the estimate of [math]\displaystyle{ \beta }[/math] is the value [math]\displaystyle{ \widehat{\beta } }[/math] that satisfies:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \sum }}\,{{n}_{i}}\left[ \frac{T_{i}^{\widehat{\beta }}\ln {{T}_{i}}-T_{i-1}^{\widehat{\beta }}\ln {{T}_{i-1}}}{T_{i}^{\widehat{\beta }}-T_{i-1}^{\widehat{\beta }}}-\ln {{T}_{k}} \right]=0 }[/math]
Grouped Data Example
Consider the grouped failure times data given in the following table. Solve for the Crow-AMSAA parameters using MLE.
| Run Number | Cumulative Failures | End Time(hr) | [math]\displaystyle{ \ln{(T_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)^2} }[/math] | [math]\displaystyle{ \ln{(\theta_i)} }[/math] | [math]\displaystyle{ \ln{(T_i)}\cdot\ln{(\theta_i)} }[/math] |
|---|---|---|---|---|---|---|
| 1 | 2 | 200 | 5.298 | 28.072 | 0.693 | 3.673 |
| 2 | 3 | 400 | 5.991 | 35.898 | 1.099 | 6.582 |
| 3 | 4 | 600 | 6.397 | 40.921 | 1.386 | 8.868 |
| 4 | 11 | 3000 | 8.006 | 64.102 | 2.398 | 19.198 |
| Sum = | 25.693 | 168.992 | 5.576 | 38.321 |
Solution
To obtain the estimator of [math]\displaystyle{ \beta }[/math] , Eqn. (vv) must be solved numerically for [math]\displaystyle{ \beta }[/math] . Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is [math]\displaystyle{ 0.6315 }[/math] . Now plugging this value into Eqn. (vv1), the estimator of [math]\displaystyle{ \lambda }[/math] is:
- [math]\displaystyle{ \begin{align} & \widehat{\lambda }= & \frac{11}{3,{{000}^{0.6315}}} \\ & = & 0.0701 \end{align} }[/math]
Therefore, the intensity function becomes:
- [math]\displaystyle{ \widehat{\rho }(T)=0.0701\cdot 0.6315\cdot {{T}^{-0.3685}} }[/math]
Grouped Data Confidence Bounds
Template loop detected: Template:Bounds on beta camsaa-gd
Template loop detected: Template:Bounds on lambda camsaa-gd
Template loop detected: Template:Bounds on growth rate camsaa-gd
Template loop detected: Template:Bounds on cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given cumulative mtbf camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous mtbf camsaa-gd
Template loop detected: Template:Bounds on time given cumulative failure intensity camsaa-gd
Template loop detected: Template:Bounds on time given instantaneous failure intensity camsaa-gd
Template loop detected: Template:Bounds on cumulative number of failures camsaa-gd
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.
Another Grouped Data Example
A new helicopter system is under development. System failure data has been collected on five helicopters during the final test phase. The actual failure times cannot be determined since the failures are not discovered until after the helicopters are brought into the maintenance area. However, total flying hours are known when the helicopters are brought in for service and every two weeks, each helicopter undergoes a thorough inspection to uncover any failures that may have occurred since the last inspection. Therefore, the cumulative total number of flight hours and the cumulative total number of failures for the five helicopters are known for each two-week period. The total number of flight hours from the test phase is 500, which was accrued over a period of 12 weeks (6 2-week intervals). For each 2-week interval, the total number of flight hours and total number of failures for the five helicopters were recorded. The grouped data set is displayed in the following table.
| Interval | Interval Length | Failures in Interval |
|---|---|---|
| 1 | 0 - 62 | 12 |
| 2 | 62 -100 | 6 |
| 3 | 100 - 187 | 15 |
| 4 | 187 - 210 | 3 |
| 5 | 210 - 350 | 18 |
| 6 | 350 - 500 | 16 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Calculate the confidence bounds on the cumulative and instantaneous MTBF using the
Fisher Matrix and Crow methods.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using Eqn. (vv). Using RGA, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.81361. Now plug this value into Eqn. (vv1) and [math]\displaystyle{ \widehat{\lambda } }[/math] is:
- [math]\displaystyle{ \widehat{\lambda }=0.44585 }[/math]
Fisher Matrix confidence bounds can be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level by:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 0.6546 \\ & {{\beta }_{U}}= & \hat{\beta }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\beta })}/\hat{\beta }}} \\ & = & 1.0112 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \hat{\lambda }{{e}^{{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 0.14594 \\ & {{\lambda }_{U}}= & \hat{\lambda }{{e}^{-{{z}_{\alpha }}\sqrt{Var(\hat{\lambda })}/\hat{\lambda }}} \\ & = & 1.36207 \end{align} }[/math]
Crow confidence bounds can also be obtained on the parameters [math]\displaystyle{ \widehat{\beta } }[/math] and [math]\displaystyle{ \widehat{\lambda } }[/math] at the 90% confidence level, as:
- [math]\displaystyle{ \begin{align} & {{\beta }_{L}}= & \hat{\beta }(1-S) \\ & = & 0.63552 \\ & {{\beta }_{U}}= & \hat{\beta }(1+S) \\ & = & 0.99170 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{\lambda }_{L}}= & \frac{\chi _{\tfrac{\alpha }{2},2N}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.36197 \\ & {{\lambda }_{U}}= & \frac{\chi _{1-\tfrac{\alpha }{2},2N+2}^{2}}{2\cdot T_{k}^{\beta }} \\ & = & 0.53697 \end{align} }[/math]
- 2) The Fisher Matrix confidence bounds for the cumulative MTBF and the instantaneous MTBF at the 90% 2-sided confidence level and for [math]\displaystyle{ T=500 }[/math] hr are:
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & {{{\hat{m}}}_{c}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 5.8680 \\ & {{[{{m}_{c}}(T)]}_{U}}= & {{{\hat{m}}}_{c}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{c}}(t))}/{{{\hat{m}}}_{c}}(t)}} \\ & = & 8.6947 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{{\hat{m}}}_{i}}(t){{e}^{{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 6.6483 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{{\hat{m}}}_{i}}(t){{e}^{-{{z}_{\alpha /2}}\sqrt{Var({{{\hat{m}}}_{i}}(t))}/{{{\hat{m}}}_{i}}(t)}} \\ & = & 11.5932 \end{align} }[/math]
The next two figures show plots of the Fisher Matrix confidence bounds for the cumulative and instantaneous MTBF.
The Crow confidence bounds for the cumulative and instantaneous MTBF at the 90% 2-sided confidence level and for hours are:
- [math]\displaystyle{ T=500 }[/math]
- [math]\displaystyle{ \begin{align} & {{[{{m}_{c}}(T)]}_{L}}= & \frac{1}{C{{(t)}_{U}}} \\ & = & 5.85449 \\ & {{[{{m}_{c}}(T)]}_{U}}= & \frac{1}{C{{(t)}_{L}}} \\ & = & 8.79822 \end{align} }[/math]
- and:
- [math]\displaystyle{ \begin{align} & {{[MTB{{F}_{i}}]}_{L}}= & {{\widehat{m}}_{i}}(1-W) \\ & = & 6.19623 \\ & {{[MTB{{F}_{i}}]}_{U}}= & {{\widehat{m}}_{i}}(1+W) \\ & = & 11.36223 \end{align} }[/math]
The next two figures show plots of the Crow confidence bounds for the cumulative and instantaneous MTBF.
Goodness-of-Fit Tests
While using the Crow-AMSAA model in the RGA 7 software, there are four goodness-of-fit tests which may become available depending on their applicability. The Cramér-von Mises goodness-of-fit test tests the hypothesis that the data follows a nonhomogeneous Poisson process with failure intensity equal to [math]\displaystyle{ u(t)=\lambda \beta {{t}^{\beta -1}} }[/math] . This test can be applied when the failure data is complete over the continuous interval [math]\displaystyle{ [0,{{T}_{q}}] }[/math] with no gaps in the data. The Chi-Squared test is a goodness-of-fit test that can be applied under more general circumstances, particularly when the data set is grouped. In addition, for multiple system data the Common Beta Hypothesis (CBH) test also can be used to compare the intensity functions of the individual systems by comparing the [math]\displaystyle{ {{\beta }_{q}} }[/math] results for each system. Lastly, the Laplace Trend test checks for trends within the data. Due to their general application to multiple models, the Common Beta Hypothesis test and the Laplace Trend test are both presented in Appendix B. The Cramér-von Mises and Chi-Squared tests are described here since they apply to the Crow-AMSAA model only.
Cramér-von Mises Test for Individual Failure Times
If the individual failure times are known, a Cramér-von Mises statistic is used to test the null hypothesis that a non-homogeneous Poisson process with failure intensity function [math]\displaystyle{ \rho \left( t \right)=\lambda \,\beta \,{{t}^{\beta -1}}\left( \lambda \gt 0,\beta \gt 0,t\gt 0 \right) }[/math] properly describes the reliability growth of a system. The Cramér-von Mises goodness-of-fit statistic is then given by the following expression:
- [math]\displaystyle{ C_{M}^{2}=\frac{1}{12M}+\underset{i=1}{\overset{M}{\mathop \sum }}\,{{\left[ {{\left( \frac{{{T}_{i}}}{T} \right)}^{{\hat{\beta }}}}-\frac{2i-1}{2M} \right]}^{2}} }[/math]
- where:
- [math]\displaystyle{ M=\left\{ \begin{matrix} N\text{ if the test is time terminated} \\ N-1\text{ if the test is failure terminated} \\ \end{matrix} \right\} }[/math]
The failure times, [math]\displaystyle{ {{T}_{i}} }[/math] , must be ordered so that [math]\displaystyle{ {{T}_{1}}\lt {{T}_{2}}\lt \ldots \lt {{T}_{M}} }[/math] . If the statistic [math]\displaystyle{ C_{M}^{2} }[/math] exceeds the critical value corresponding to [math]\displaystyle{ M }[/math] for a chosen significance level, then the null hypothesis that the Crow-AMSAA model adequately fits the data shall be rejected. Otherwise, the model shall be accepted. Critical values of [math]\displaystyle{ C_{M}^{2} }[/math] are shown in Appendix B, Table B.2, where the table is indexed by the total number of observed failures, [math]\displaystyle{ M }[/math] .
Chi-Squared Test for Grouped Data
A Chi-Squared goodness-of-fit test is used to test the null hypothesis that the Crow-AMSAA reliability model adequately represents a set of grouped data. The expected number of failures in the interval from [math]\displaystyle{ {{T}_{i-1}} }[/math] to [math]\displaystyle{ {{T}_{i}} }[/math] is approximated by:
- [math]\displaystyle{ {{\widehat{\theta }}_{i}}=\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right) }[/math]
For each interval, [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] shall not be less than 5 and, if necessary, adjacent intervals may have to be combined so that the expected number of failures in any combined interval is at least 5. Let the number of intervals after this recombination be [math]\displaystyle{ d }[/math] and let the observed number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{N}_{i}} }[/math] and let the expected number of failures in the [math]\displaystyle{ {{i}^{th}} }[/math] new interval be [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] . Then the following statistic is approximately distributed as a Chi-Squared random variable with degrees of freedom [math]\displaystyle{ d-2 }[/math] .
- [math]\displaystyle{ {{\chi }^{2}}=\underset{i=1}{\overset{d}{\mathop \sum }}\,\frac{{{({{N}_{i}}-{{\widehat{\theta }}_{i}})}^{2}}}{{{\widehat{\theta }}_{i}}} }[/math]
The null hypothesis is rejected if the [math]\displaystyle{ {{\chi }^{2}} }[/math] statistic exceeds the critical value for a chosen significance level. This means that the hypothesis that the Crow-AMSAA model adequately fits the grouped data shall be rejected. Critical values for this statistic can be found in tables of the Chi-Squared distribution.
Goodness-of-Fit Test Example
An aircraft has scheduled inspections at intervals of 20 flight hours. The following table gives the data set from the first 100 hours of flight testing.
| Start Time | End Time | Number of Failures |
|---|---|---|
| 0 | 20 | 13 |
| 20 | 40 | 16 |
| 40 | 60 | 5 |
| 60 | 80 | 8 |
| 80 | 100 | 7 |
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Evaluate the goodness-of-fit.
Solution
- 1) Obtain the estimator of [math]\displaystyle{ \beta }[/math] using the equation given above for Grouped Data. Using the RGA software, the value of [math]\displaystyle{ \widehat{\beta } }[/math] is 0.75285. Now plug this value into the [math]\displaystyle{ \widehat{\lambda } }[/math] equation from that section to get:
- [math]\displaystyle{ \widehat{\lambda }=1.52931 }[/math]
- 2) There are a total of [math]\displaystyle{ M=49 }[/math]observed failures from [math]\displaystyle{ d=5 }[/math] intervals. The following table shows that those adjacent intervals do not have to be combined after applying the [math]\displaystyle{ {{\widehat{\theta }}_{i}} }[/math] equation (from the Chi-Squared Test for Grouped Datasection) to the original intervals.
| Start Time | End Time | Observed Number of Failures | Expected Number of Failures |
|---|---|---|---|
| 0 | 20 | 13 | 14.59 |
| 20 | 40 | 16 | 9.99 |
| 40 | 60 | 5 | 8.77 |
| 60 | 80 | 8 | 8.07 |
| 80 | 100 | 7 | 7.58 |
To test the model's goodness-of-fit, a Chi-Squared statistic of 5.45 is compared to the critical value of 7.8 corresponding to 3 degrees of freedom and a 0.05 significance level. Since the statistic is less than the critical value, the applicability of the Crow-AMSAA model is accepted.
Missing Data
Most of the reliability growth models used for estimating and tracking reliability growth based on test data assume that the data set represents all actual system failure times consistent with a uniform definition of failure (complete data). In practice, this may not always be the case and may result in too few or too many failures being reported over some interval of test time. This may result in distorted estimates of the growth rate and current system reliability. This section discusses a practical reliability growth estimation and analysis procedure based on the assumption that anomalies may exist within the data over some interval of the test period but the remaining failure data follows the Crow-AMSAA reliability growth model. In particular, it is assumed that the beginning and ending points in which the anomalies lie are generated independently of the underlying reliability growth process. The approach for estimating the parameters of the growth model with problem data over some interval of time is basically to not use this failure information. The analysis retains the contribution of the interval to the total test time, but no assumptions are made regarding the actual number of failures over the interval. This is often referred to as gap analysis.
Consider the case where a system is tested for time [math]\displaystyle{ T }[/math] and the actual failure times are recorded. The time [math]\displaystyle{ T }[/math] may possibly be an observed failure time. Also, the end points of the gap interval may or may not correspond to a recorded failure time. The underlying assumption is that the data used in the maximum likelihood estimation follows the Crow-AMSAA model with a Weibull intensity function [math]\displaystyle{ \lambda \beta {{t}^{\beta -1}} }[/math] . It is not assumed that zero failures occurred during the gap interval. Rather, it is assumed that the actual number of failures is unknown, and hence no information at all regarding these failure is used to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Let [math]\displaystyle{ {{S}_{1}} }[/math] , [math]\displaystyle{ {{S}_{2}} }[/math] denote the end points of the gap interval, [math]\displaystyle{ {{S}_{1}}\lt {{S}_{2}}. }[/math] Let [math]\displaystyle{ 0\lt {{X}_{1}}\lt {{X}_{2}}\lt \ldots \lt {{X}_{{{N}_{1}}}}\le {{S}_{1}} }[/math] be the failure times over [math]\displaystyle{ (0,\,{{S}_{1}}) }[/math] and let [math]\displaystyle{ {{S}_{2}}\lt {{Y}_{1}}\lt {{Y}_{2}}\lt \ldots \lt {{Y}_{{{N}_{1}}}}\le T }[/math] be the failure times over [math]\displaystyle{ ({{S}_{2}},\,T) }[/math] . The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] satisfying the following equations.
- [math]\displaystyle{ \widehat{\lambda }=\frac{{{N}_{1}}+{{N}_{2}}}{S\widehat{_{1}^{\beta }}+{{T}^{\widehat{\beta }}}-S_{2}^{\widehat{\beta }}} }[/math]
- [math]\displaystyle{ \widehat{\beta }=\frac{{{N}_{1}}+{{N}_{2}}}{\widehat{\lambda }\left[ S\widehat{_{1}^{\beta }}\ln {{S}_{1}}+{{T}^{\widehat{\beta }}}\ln T-S_{2}^{\widehat{\beta }}\ln {{S}_{2}} \right]-\left[ \underset{i=1}{\overset{{{N}_{1}}}{\mathop{\sum }}}\,\ln {{X}_{i}}+\underset{i=1}{\overset{{{N}_{2}}}{\mathop{\sum }}}\,\ln {{Y}_{i}} \right]} }[/math]
In general, these equations cannot be solved explicitly for [math]\displaystyle{ \widehat{\lambda } }[/math] and [math]\displaystyle{ \widehat{\beta } }[/math] , but must be solved by an iterative procedure.
Missing Data Example
Consider a system under development that was subjected to a reliability growth test for [math]\displaystyle{ T=1,000 }[/math] hours. Each month, the successive failure times on a cumulative test time basis were reported. According to the test plan, 125 hours of test time were accumulated on each prototype system each month. The total reliability growth test program lasted for 7 months. One prototype was tested for each of the months 1, 3, 4, 5, 6 and 7 with 125 hours of test time. During the second month, two prototypes were tested for a total of 250 hours of test time. The next table shows the successive [math]\displaystyle{ N=86 }[/math] failure times that were reported for [math]\displaystyle{ T=1000 }[/math] hours of testing.
| .5 | .6 | 10.7 | 16.6 | 18.3 | 19.2 | 19.5 | 25.3 |
| 39.2 | 39.4 | 43.2 | 44.8 | 47.4 | 65.7 | 88.1 | 97.2 |
| 104.9 | 105.1 | 120.8 | 195.7 | 217.1 | 219 | 257.5 | 260.4 |
| 281.3 | 283.7 | 289.8 | 306.6 | 328.6 | 357.0 | 371.7 | 374.7 |
| 393.2 | 403.2 | 466.5 | 500.9 | 501.5 | 518.4 | 520.7 | 522.7 |
| 524.6 | 526.9 | 527.8 | 533.6 | 536.5 | 542.6 | 543.2 | 545.0 |
| 547.4 | 554.0 | 554.1 | 554.2 | 554.8 | 556.5 | 570.6 | 571.4 |
| 574.9 | 576.8 | 578.8 | 583.4 | 584.9 | 590.6 | 596.1 | 599.1 |
| 600.1 | 602.5 | 613.9 | 616.0 | 616.2 | 617.1 | 621.4 | 622.6 |
| 624.7 | 628.8 | 642.4 | 684.8 | 731.9 | 735.1 | 753.6 | 792.5 |
| 803.7 | 805.4 | 832.5 | 836.2 | 873.2 | 975.1 |
The observed and cumulative number of failures for each month are:
| Month | Time Period | Observed Failure Times | Cumulative Failure Times |
|---|---|---|---|
| 1 | 0-125 | 19 | 19 |
| 2 | 125-375 | 13 | 32 |
| 3 | 375-500 | 3 | 35 |
| 4 | 500-625 | 38 | 73 |
| 5 | 625-750 | 5 | 78 |
| 6 | 750-875 | 7 | 85 |
| 7 | 875-1000 | 1 | 86 |
- 1) Determine the maximum likelihood estimators for the Crow-AMSAA model.
- 2) Evaluate the goodness-of-fit for the model.
- 3) Consider [math]\displaystyle{ (500,\ 625) }[/math] as the gap interval and determine the maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] .
Solution
- 1) For the time terminated test:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.7597 \\ & \widehat{\lambda }= & 0.4521 \end{align} }[/math]
- 2) The Cramér-von Mises goodness-of-fit test for this data set yields:
- [math]\displaystyle{ C_{M}^{2}=\tfrac{1}{12M}+\underset{i=1}{\overset{M}{\mathop{\sum }}}\,{{\left[ (\tfrac{{{T}_{i}}}{T})\widehat{^{\beta }}-\tfrac{2i-1}{2M} \right]}^{2}}= }[/math] [math]\displaystyle{ 0.6989 }[/math]
The critical value at the 10% significance level is 0.173. Therefore, the test indicated that the analyst should reject the hypothesis that the data set follows the Crow-AMSAA reliability growth model. Figure 4fig814 is a plot of [math]\displaystyle{ \ln N(t) }[/math] versus [math]\displaystyle{ \ln t }[/math] with the fitted line [math]\displaystyle{ \ln \hat{\lambda }+\hat{\beta }\ln t }[/math] , where [math]\displaystyle{ \widehat{\lambda }=0.4521 }[/math] and [math]\displaystyle{ \widehat{\beta }=0.7597 }[/math] are the maximum likelihood estimates. Observing the data during the fourth month (between 500 and 625 hr), 38 failures were reported. This number is very high in comparison to the failures reported in the other months. A quick investigation found that a number of new data collectors were assigned to the project during this month. It was also discovered that extensive design changes were made during this period, which involved the removal of a large number of parts. It is possible that these removals, which were not failures, were incorrectly reported as failed parts. Based on knowledge of the system and the test program, it was clear that such a large number of actual system failures was extremely unlikely. The consensus was that this anomaly was due to the failure reporting. It was decided that the actual number of failures over this month would be assumed for this analysis to be unknown but consistent with the remaining data and the Crow-AMSAA reliability growth model.
- 3) Considering the problem interval [math]\displaystyle{ (500,625) }[/math] as the gap interval, we will use the data over the interval [math]\displaystyle{ (0,500) }[/math] and over the interval [math]\displaystyle{ (625,1000). }[/math] Eqns. (gaplambda) and (gapbeta) are the appropriate equations to estimate [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] since the failure times are known. In this case [math]\displaystyle{ {{S}_{1}}=500,\,{{S}_{2}}=625 }[/math] and [math]\displaystyle{ T=1000,\ {{N}_{1}}=35,\,{{N}_{2}}=13. }[/math] The maximum likelihood estimates of [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are:
- [math]\displaystyle{ \begin{align} & \widehat{\beta }= & 0.5596 \\ & \widehat{\lambda }= & 1.1052 \end{align} }[/math]
The next figure is a plot of the cumulative number of failures versus time. This plot is approximately linear, which also indicates a good fit of the model.
Crow Discrete Reliability Growth Model
The Crow-AMSAA model can be adapted for the analysis of success/failure data (also called "discrete" or "attribute" data). Suppose system development is represented by [math]\displaystyle{ i }[/math] configurations. This corresponds to [math]\displaystyle{ i-1 }[/math] configuration changes, unless fixes are applied at the end of the test phase, in which case there would be [math]\displaystyle{ i }[/math] configuration changes. Let [math]\displaystyle{ {{N}_{i}} }[/math] be the number of trials during configuration [math]\displaystyle{ i }[/math] and let [math]\displaystyle{ {{M}_{i}} }[/math] be the number of failures during configuration [math]\displaystyle{ i }[/math] . Then the cumulative number of trials through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{T}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{N}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{T}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{N}_{i}} }[/math]
And the cumulative number of failures through configuration [math]\displaystyle{ i }[/math] , namely [math]\displaystyle{ {{K}_{i}} }[/math] , is the sum of the [math]\displaystyle{ {{M}_{i}} }[/math] for all [math]\displaystyle{ i }[/math] , or:
- [math]\displaystyle{ {{K}_{i}}=\underset{}{\overset{}{\mathop \sum }}\,{{M}_{i}} }[/math]
The expected value of [math]\displaystyle{ {{K}_{i}} }[/math] can be expressed as [math]\displaystyle{ E[{{K}_{i}}] }[/math] and defined as the expected number of failures by the end of configuration [math]\displaystyle{ i }[/math] . Applying the learning curve property to [math]\displaystyle{ E[{{K}_{i}}] }[/math] implies:
- [math]\displaystyle{ E\left[ {{K}_{i}} \right]=\lambda T_{i}^{\beta } }[/math]
Denote [math]\displaystyle{ {{f}_{1}} }[/math] as the probability of failure for configuration 1 and use it to develop a generalized equation for [math]\displaystyle{ {{f}_{i}} }[/math] in terms of the [math]\displaystyle{ {{T}_{i}} }[/math] and [math]\displaystyle{ {{N}_{i}} }[/math] . From Eqn. (expectedn), the expected number of failures by the end of configuration 1 is:
- [math]\displaystyle{ E\left[ {{K}_{1}} \right]=\lambda T_{1}^{\beta }={{f}_{1}}{{N}_{1}} }[/math]
- [math]\displaystyle{ \therefore {{f}_{1}}=\frac{\lambda T_{1}^{\beta }}{{{N}_{1}}} }[/math]
Applying Eqn. (expectedn) again and noting that the expected number of failures by the end of configuration 2 is the sum of the expected number of failures in configuration 1 and the expected number of failures in configuration 2:
- [math]\displaystyle{ \begin{align} & E\left[ {{K}_{2}} \right]= & \lambda T_{2}^{\beta } \\ & = & {{f}_{1}}{{N}_{1}}+{{f}_{2}}{{N}_{2}} \\ & = & \lambda T_{1}^{\beta }+{{f}_{2}}{{N}_{2}} \end{align} }[/math]
- [math]\displaystyle{ \therefore {{f}_{2}}=\frac{\lambda T_{2}^{\beta }-\lambda T_{1}^{\beta }}{{{N}_{2}}} }[/math]
By this method of inductive reasoning, a generalized equation for the failure probability on a configuration basis, [math]\displaystyle{ {{f}_{i}} }[/math] , is obtained, such that:
- [math]\displaystyle{ {{f}_{i}}=\frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} }[/math]
For the special case where [math]\displaystyle{ {{N}_{i}}=1 }[/math] for all [math]\displaystyle{ i }[/math] , Eqn. (dfi) becomes a smooth curve, [math]\displaystyle{ {{g}_{i}} }[/math] , that represents the probability of failure for trial by trial data, or:
- [math]\displaystyle{ {{g}_{i}}=\lambda \cdot {{i}^{\beta }}-\lambda \cdot {{\left( i-1 \right)}^{\beta }} }[/math]
In Eqn. (dfi1), [math]\displaystyle{ i }[/math] represents the trial number. Thus using Eqn. (dfi), an equation for the reliability (probability of success) for the [math]\displaystyle{ {{i}^{th}} }[/math] configuration is obtained:
- [math]\displaystyle{ {{R}_{i}}=1-{{f}_{i}} }[/math]
And using Eqn. (dfi1), the equation for the reliability for the [math]\displaystyle{ {{i}^{th}} }[/math] trial is:
- [math]\displaystyle{ {{R}_{i}}=1-{{g}_{i}} }[/math]
Maximum Likelihood Estimators for Discrete Model
This section describes procedures for estimating the parameters of the Crow-AMSAA model for success/failure data. An example is presented illustrating these concepts. The estimation procedures described below provide maximum likelihood estimates (MLEs) for the model's two parameters, [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] . The MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] allow for point estimates for the probability of failure, given by:
- [math]\displaystyle{ {{\hat{f}}_{i}}=\frac{\hat{\lambda }T_{i}^{{\hat{\beta }}}-\hat{\lambda }T_{i-1}^{{\hat{\beta }}}}{{{N}_{i}}}=\frac{\hat{\lambda }\left( T_{i}^{{\hat{\beta }}}-T_{i-1}^{{\hat{\beta }}} \right)}{{{N}_{i}}} }[/math]
And the probability of success (reliability) for each configuration [math]\displaystyle{ i }[/math] is equal to:
- [math]\displaystyle{ {{\hat{R}}_{i}}=1-{{\hat{f}}_{i}} }[/math]
The likelihood function is:
- [math]\displaystyle{ \underset{i=1}{\overset{k}{\mathop \prod }}\,\left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right){{\left( \frac{\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{M}_{i}}}}{{\left( \frac{{{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta }}{{{N}_{i}}} \right)}^{{{N}_{i}}-{{M}_{i}}}} }[/math]
Taking the natural log on both sides yields:
- [math]\displaystyle{ \begin{align} & \Lambda = & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ \ln \left( \begin{matrix} {{N}_{i}} \\ {{M}_{i}} \\ \end{matrix} \right)+{{M}_{i}}\left[ \ln (\lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \\ & & +\underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ ({{N}_{i}}-{{M}_{i}})\left[ \ln ({{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta })-\ln {{N}_{i}} \right] \right] \end{align} }[/math]
Taking the derivative with respect to [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] respectively, exact MLEs for [math]\displaystyle{ \lambda }[/math] and [math]\displaystyle{ \beta }[/math] are values satisfying the following two equations:
- [math]\displaystyle{ \begin{align} & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{H}_{i}}\times {{S}_{i}}= & 0 \\ & \underset{i=1}{\overset{K}{\mathop \sum }}\,{{U}_{i}}\times {{S}_{i}}= & 0 \end{align} }[/math]
- where:
- [math]\displaystyle{ \begin{align} & {{H}_{i}}= & \underset{i=1}{\overset{K}{\mathop \sum }}\,\left[ T_{i}^{\beta }\ln {{T}_{i}}-T_{i-1}^{\beta }\ln {{T}_{i-1}} \right] \\ & {{S}_{i}}= & \frac{{{M}_{i}}}{\left[ \lambda T_{i}^{\beta }-\lambda T_{i-1}^{\beta } \right]}-\frac{{{N}_{i}}-{{M}_{i}}}{\left[ {{N}_{i}}-\lambda T_{i}^{\beta }+\lambda T_{i-1}^{\beta } \right]} \\ & {{U}_{i}}= & T_{i}^{\beta }-T_{i-1}^{\beta }\, \end{align} }[/math]
Discrete Model Example
A one-shot system underwent reliability growth development testing for a total of 68 trials. Delayed corrective actions were incorporated after the 14th, 33rd and 48th trials. From trial 49 to trial 68, the configuration was not changed.
- Configuration 1 experienced 5 failures,
- Configuration 2 experienced 3 failures,
- Configuration 3 experienced 4 failures and
- Configuration 4 experienced 4 failures.
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Estimate the unreliability and reliability by configuration.
Solution
- 1) The solution of MLE equations above yield [math]\displaystyle{ \lambda = 0.5954 }[/math] and [math]\displaystyle{ \beta =0.7801 }[/math].
- 2) The following table displays the results for probability of failure and reliability, and these results are displayed in the next two plots
| Configuration([math]\displaystyle{ i }[/math]) | Estimated Failure Probability | Estimated Reliability |
|---|---|---|
| 1 | 0.333 | 0.667 |
| 2 | 0.234 | 0.766 |
| 3 | 0.206 | 0.794 |
| 4 | 0.190 | 0.810 |
Discrete Model for Mixed Data
In the RGA software, the Discrete Data > Mixed Data option gives a data sheet that can have input data that is either configuration in groups or individual trial by trial, or a mixed combination of individual trials and configurations of more than one trial. The calculations use the same mathematical methods described above in the Grouped Data section.
Mixed Data Example
The table below shows the number of failures of each interval of trials and the cumulative number of trials in each interval for a reliability growth test. For example, the first row indicates that for an interval of 14 trials, 5 failures occurred.
| Failures in Interval | Cumulative Trials |
|---|---|
| 5 | 14 |
| 3 | 33 |
| 4 | 48 |
| 0 | 52 |
| 1 | 53 |
| 0 | 57 |
| 1 | 58 |
| 0 | 62 |
| 1 | 63 |
| 0 | 67 |
| 1 | 68 |
Using the RGA software, the parameters of the Crow-AMSAA model are estimated as follows:
- [math]\displaystyle{ \widehat{\beta }=0.7950 }[/math]
- and:
- [math]\displaystyle{ \widehat{\lambda }=0.5588 }[/math]
As we have seen, the Crow-AMSAA instantaneous failure intensity, [math]\displaystyle{ {{\lambda }_{i}}(T) }[/math] , is defined as:
- [math]\displaystyle{ {{\lambda }_{i}}(T)=\lambda \beta {{T}^{\beta -1}},\text{with }T\gt 0,\text{ }\lambda \gt 0\text{ and }\beta \gt 0 }[/math]
Using the above parameter estimates, we can calculate the or instantaneous unreliability at the end of the test, or [math]\displaystyle{ T=68. }[/math]
- [math]\displaystyle{ {{R}_{i}}(68)=0.5588\cdot 0.7950\cdot {{68}^{0.7950-1}}=0.1871 }[/math]
This result that can be obtained from the Quick Calculation Pad (QCP), for [math]\displaystyle{ T=68, }[/math] as seen in the following picture.
The instantaneous reliability can then be calculated as:
- [math]\displaystyle{ {{R}_{inst}}=1-0.1871=0.8129 }[/math]
The average unreliability is calculated as:
- [math]\displaystyle{ \text{Average Unreliability }({{t}_{1,}}{{t}_{2}})=\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
and the average reliability is calculated as:
- [math]\displaystyle{ \text{Average Reliability }({{t}_{1,}}{{t}_{2}})=1-\frac{\lambda t_{2}^{\beta }-\lambda t_{1}^{\beta }}{{{t}_{2}}-{{t}_{1}}} }[/math]
Mixed Data Confidence Bounds
Bounds on Average Failure Probability for Mixed Data
The process to calculate the average unreliability confidence bounds for mixed data is as follows:
- 1) Calculate the average failure probability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
- 2) There will exist a [math]\displaystyle{ {{t}^{*}}\,\! }[/math] between [math]\displaystyle{ {{t}_{1}}\,\! }[/math] and [math]\displaystyle{ {{t}_{2}}\,\! }[/math] such that the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] equals the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math]. The confidence intervals for the instantaneous unreliability at [math]\displaystyle{ {{t}^{*}}\,\! }[/math] are the confidence intervals for the average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math].
Bounds on Average Reliability for Mixed Data
The process to calculate the average reliability confidence bounds for mixed data is as follows:
- 1) Calculate confidence bounds for average unreliability [math]\displaystyle{ ({{t}_{1}},{{t}_{2}})\,\! }[/math] as described above.
- 2) The confidence bounds for reliability are 1 minus these confidence bounds for average unreliability.
Change of Slope
The assumption of the Crow-AMSAA (NHPP) model is that the failure intensity is monotonically increasing, decreasing or remaining constant over time. However, there might be cases in which the system design or the operational environment experiences major changes during the observation period and, therefore, a single model will not be appropriate to describe the failure behavior for the entire timeline. RGA incorporates a methodology that can be applied to scenarios where a major change occurs during a reliability growth test. The test data can be broken into two segments with a separate Crow-AMSAA (NHPP) model applied to each segment. Consider the data in Figure changeflopeisual that were obtained during a reliability growth test.
As discussed above, the cumulative number of failures vs. the cumulative time should be linear on logarithmic scales. Figure changeflopeisualog shows the data plotted on logarithmic scales.
One can easily recognize that the failure behavior is not constant throughout the duration of the test. Just by observing the data, it can be asserted that a major change occurred at around [math]\displaystyle{ 140 }[/math] hours that resulted in a change in the rate of failures. Therefore, using a single model to analyze this data set likely will not be appropriate.
The Change of Slope methodology proposes to split the data into two segments and apply a Crow-AMSAA (NHPP) model to each segment. The time of change that will be used to split the data into the two segments (it will be referred to as [math]\displaystyle{ {{T}_{1}} }[/math] ) could be estimated just by observing the data but will most likely be dictated by engineering knowledge of the specific change to the system design or operating conditions. It is important to note that although two separate models will be applied to each segment, the information collected in the first segment (i.e. data up to [math]\displaystyle{ {{T}_{1}} }[/math] ) will be considered when creating the model for the second segment (i.e. data after [math]\displaystyle{ {{T}_{1}} }[/math] ). The models presented next can be applied to the reliability growth analysis of a single system or multiple systems.
Model for First Segment
(Data up to [math]\displaystyle{ {{T}_{1}} }[/math] )
The data up to the point of the change that occurs at [math]\displaystyle{ {{T}_{1}} }[/math] will be analyzed using the Crow-AMSAA (NHPP) model. Based on Eqns. (amsaa5) and (amsaa6), the ML estimators of the model are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}} }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln {{t}_{i}}} }[/math]
- where:
- [math]\displaystyle{ {{T}_{1}} }[/math] is the time when the change occurs.
- [math]\displaystyle{ {{n}_{1}} }[/math] is the number of failures observed up to time [math]\displaystyle{ {{T}_{1}}. }[/math]
- [math]\displaystyle{ {{t}_{i}} }[/math] is the time at which each corresponding failure was observed.
Eqn. (beta1) can be rewritten as follows:
- [math]\displaystyle{ \begin{align} & {{\widehat{\beta }}_{1}}= & \frac{{{n}_{1}}}{{{n}_{1}}\ln {{T}_{1}}-\left( \ln {{t}_{1}}+\ln {{t}_{2}}+...+\ln {{t}_{{{n}_{1}}}} \right)} \\ & = & \frac{{{n}_{1}}}{(\ln {{T}_{1}}-\ln {{t}_{1}})+(\ln {{T}_{1}}-\ln {{t}_{2}})+(...)+(\ln {{T}_{1}}-\ln {{t}_{{{n}_{1}}}})} \\ & = & \frac{{{n}_{1}}}{\ln \tfrac{{{T}_{1}}}{{{t}_{1}}}+\ln \tfrac{{{T}_{1}}}{{{t}_{2}}}+...+\ln \tfrac{{{T}_{1}}}{{{t}_{{{n}_{1}}}}}} \end{align} }[/math]
- or
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}} }[/math]
Model for Second Segment
(Data after [math]\displaystyle{ {{T}_{1}} }[/math] )
The Crow-AMSAA (NHPP) model will be used again to analyze the data after [math]\displaystyle{ {{T}_{1}} }[/math] . However, the information collected during the first segment will be used when creating the model for the second segment. Given that, the ML estimators of the model parameters in the second segment are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}} }[/math]
and similar to Eqn. (beta1mallq):
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}} }[/math]
- where:
- [math]\displaystyle{ {{n}_{2}} }[/math] is the number of failures that were observed after [math]\displaystyle{ {{T}_{1}} }[/math] .
- [math]\displaystyle{ n={{n}_{1}}+{{n}_{2}} }[/math] is the total number of failures observed throughout the test.
- [math]\displaystyle{ {{T}_{2}} }[/math] is the end time of the test. The test can either be failure terminated or time terminated.
Change of Slope Example
The following table gives the failure times obtained from a reliability growth test of a newly designed system. The test has a duration of 660 hours.
First, apply a single Crow-AMSAA (NHPP) model to all of the data. The following plot shows the expected failures obtained from the model (the line) along with the observed failures (the points).
As it can be seen from the plot, the model does not seem to accurately track the data. This is confirmed by performing the Cramér-von Mises goodness-of-fit test which checks the hypothesis that the data follows a non-homogeneous Poisson process with a power law failure intensity. The model fails the goodness-of-fit test because the test statistic (0.3309) is higher than the critical value (0.1729) at the 0.1 significance level. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
Through further investigation, it is discovered that a significant design change occurred at 400 hours of test time. It is suspected that this modification is responsible for the change in the failure behavior.
In the RGA software you have the option to perform a standard Crow-AMSAA (NHPP) analysis or to apply the Change of Slope, where you can specify a specific breakpoint, as shown in the following figure. The RGA software actually creates a grouped data set where the data in Segment 1 is included and defined by a single interval to calculate the Segment 2 parameters. However, these results are equivalent to the parameters estimated using the equations presented here.
Therefore, the Change of Slope methodology is applied to break the data into two segments for analysis. The first segment is set from 0 to 400 hours and the second segment is from 401 to 660 hours (which is the end time of the test). The Crow-AMSAA (NHPP) parameters for the first segment (0-400 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{1}}}=\frac{{{n}_{1}}}{T_{1}^{{{\beta }_{1}}}}=\frac{50}{{{400}^{1.0359}}}=0.1008 }[/math]
- and
- [math]\displaystyle{ {{\widehat{\beta }}_{1}}=\frac{{{n}_{1}}}{\underset{i=1}{\overset{{{n}_{1}}}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{1}}}{{{t}_{i}}}}=\frac{50}{\underset{i=1}{\overset{50}{\mathop{\sum }}}\,\ln \tfrac{400}{{{t}_{i}}}}=1.0359 }[/math]
The Crow-AMSAA (NHPP) parameters for the second segment (401-660 hours) are:
- [math]\displaystyle{ \widehat{{{\lambda }_{2}}}=\frac{{{n}_{2}}}{T_{2}^{{{\beta }_{2}}}}=\frac{58}{{{660}^{0.2971}}}=8.4304 }[/math]
- [math]\displaystyle{ {{\widehat{\beta }}_{2}}=\frac{{{n}_{2}}}{{{n}_{1}}\ln \tfrac{{{T}_{2}}}{{{T}_{1}}}+\underset{i={{n}_{1}}+1}{\overset{n}{\mathop{\sum }}}\,\ln \tfrac{{{T}_{2}}}{{{t}_{i}}}}=\frac{8}{50\ln \tfrac{660}{400}+\underset{i=51}{\overset{58}{\mathop{\sum }}}\,\ln \tfrac{660}{{{T}_{i}}}}=0.2971 }[/math]
The following figure shows a plot of the two-segment analysis along with the observed data. It is obvious that the "Change of Slope" method tracks the data more accurately.
This can also be verified by performing a Chi-Squared goodness-of-fit test. The Chi-Squared statistic is 1.2956, which is lower than the critical value of 12.017 at the 0.1 significance level; therefore, the analysis passes the test. The next figure shows a customized report that displays both the calculated parameters and the statistical test results.
When you have a model that fits the data, it can be used to make accurate predictions and calculations. Metrics such as the demonstrated MTBF at the end of the test or the expected number of failures at later times can be calculated. For example, the following plot shows the instantaneous MTBF vs. time, together with the two-sided 90% confidence bounds. Note that confidence bounds are available for the second segment only. For times up to 400 hours, the parameters of the first segment were used to calculate the MTBF; while the parameters of the second segment were used for times after 400 hours. Also note that the number of failures at the end of segment 1 is not assumed to be equal to the number of failures at the start of segment 2. This can result in a visible jump in the plot, as in this example.
The next figure shows the use of the Quick Calculation Pad (QCP) in the RGA software to calculate the Demonstrated MTBF at the end of the test (instantaneous MTBF at time = 660), together with the two-sided 90% confidence bounds. All the calculations were based on the parameters of the second segment.
More Examples
Estimating the Number of Failures if Testing Continues
Six systems were subjected to a reliability growth test and a total of 81 failures were observed. The following table presents the start and end times, along with the times-to-failure for each system. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) How many additional failures would be generated if testing continues until 3000 hours?
| System | 1 | 2 | 3 | 4 | 5 | 6 |
| Start Time | 0 | 0 | 0 | 0 | 0 | 0 |
| End Time | 504 | 541 | 454 | 474 | 436 | 500 |
| Times-to-Failure | 21 | 83 | 26 | 36 | 23 | 7 |
| 29 | 83 | 26 | 306 | 46 | 13 | |
| 43 | 83 | 57 | 306 | 127 | 13 | |
| 43 | 169 | 64 | 334 | 166 | 31 | |
| 43 | 213 | 169 | 354 | 169 | 31 | |
| 66 | 299 | 213 | 395 | 213 | 82 | |
| 115 | 375 | 231 | 403 | 213 | 109 | |
| 159 | 431 | 231 | 448 | 255 | 137 | |
| 199 | 231 | 456 | 369 | 166 | ||
| 202 | 231 | 461 | 374 | 200 | ||
| 222 | 304 | 380 | 210 | |||
| 248 | 383 | 415 | 220 | |||
| 248 | 422 | |||||
| 255 | 437 | |||||
| 286 | 469 | |||||
| 286 | 469 | |||||
| 304 | ||||||
| 320 | ||||||
| 348 | ||||||
| 364 | ||||||
| 404 | ||||||
| 410 | ||||||
| 429 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The number of failures can be estimated using the Quick Calculation Pad as shown next. The estimated number of failures at 3000 hours is equal to [math]\displaystyle{ 83.2451 }[/math] and 81 failures were observed during testing. Therefore, the number of additional failures generated if testing continues until 3000 hours is equal to [math]\displaystyle{ 83.2451-81=2.2451\approx 3 }[/math] .
Determining Whether a Design Meets the MTBF Goal
A prototype of a system was tested at the end of one of its design stages. The test was run for a total of 300 hours and 27 failures were observed. The table below shows the collected data set. The prototype has a design specification of an MTBF equal to 10 hours with a 90% confidence level at 300 hours. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimation.
- 2) Does the prototype meet the specified goal?
| 2.6 | 56.5 | 98.1 | 190.7 |
| 16.5 | 63.1 | 101.1 | 193 |
| 16.5 | 70.6 | 132 | 198.7 |
| 17 | 73 | 142.2 | 251.9 |
| 21.4 | 77.7 | 147.7 | 282.5 |
| 29.1 | 93.9 | 149 | 286.1 |
| 33.3 | 95.5 | 167.2 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The instantaneous MTBF with one-sided 90% confidence bounds can be calculated using the Quick Calculation Pad (QCP) as shown next. From the QCP, it is estimated that the lower limit on the MTBF at 300 hours with a 90% confidence level is equal to 10.8170 hours. Therefore, the prototype has met the specified goal.
Analyzing Mixed Data for a One-Shot System
A one-shot system underwent reliability growth development for a total of 50 trials. The test was performed as a combination of configuration in groups and individual trial by trial. The table below shows the obtained test data set. The first column specifies the number of failures that occurred in each interval and the second column the cumulative number of trials in that interval. Do the following:
- 1) Estimate the parameters of the Crow-AMSAA model using maximum likelihood estimators.
- 2) What are the instantaneous reliability and the 2-sided 90% confidence bounds at the end of the test?
- 3) Plot the cumulative reliability with 2-sided 90% confidence bounds.
- 4) If the test was continued for another 25 trials what would the expected number of additional failures be?
| Failures in Interval | Cumulative Trials | Failures in Interval | Cumulative Trials |
|---|---|---|---|
| 3 | 4 | 1 | 25 |
| 0 | 5 | 1 | 28 |
| 4 | 9 | 0 | 32 |
| 1 | 12 | 2 | 37 |
| 0 | 13 | 0 | 39 |
| 1 | 15 | 1 | 40 |
| 2 | 19 | 1 | 44 |
| 1 | 20 | 0 | 46 |
| 1 | 22 | 1 | 49 |
| 0 | 24 | 0 | 50 |
Solution
- 1) The next figure shows the parameters estimated using RGA.
- 2) The figure below shows the calculation of the instantaneous reliability with the 2-sided 90% confidence bounds. From the QCP it is estimated that the instantaneous reliability at stage 50 (or at the end of the test) is 72.6971% with an upper and lower 2-sided 90% confidence bound of 82.3627% and 39.5926% respectively.
- 3) The following plot shows the cumulative reliability with the 2-sided 90% confidence bounds.
- 4) The last figure shows the calculation of the expected number of failures after 75 trials. From the QCP it is estimated that the cumulative number of failures after 75 trials is [math]\displaystyle{ 26.3770\approx 27 }[/math] . Since 20 failures occurred in the first 50 trials, the estimated number of additional failures is 7.