BlockSim Analytical Examples: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
Line 1: Line 1:


===BlockSim Analytical Example===
Consider the following circuit:
<br>
[[Image:BS3sigma.png|thumb|center|300px|]]
<br>
The equivalent resistance must always be less than  <math>1.2\Omega </math> .
<br>
Draw the reliability block diagram for this circuit.
====Solution====
First, let's consider the case where all three resistors operate:
<br>
::<math>\begin{align}
\frac{1}{{{r}_{eq}}}= & \frac{1}{{{r}_{1}}}+\frac{1}{{{r}_{2}}}+\frac{1}{{{r}_{3}}} \\
= & \frac{1}{3}+\frac{1}{3}+\frac{1}{3} \\
= & 1\Omega 
\end{align}</math>
<br>
Thus, when all components operate, the equivalent resistance is  <math>1\Omega </math> , which is less than the maximum resistance of  <math>1.2\Omega </math> . 
<br>
Next, consider the case where one of the resistors fails open.  In this case, the resistance for the resistor is infinite and the equivalent resistance is:
<br>
::<math>\frac{1}{{{r}_{eq}}}=\frac{1}{\infty }+\frac{1}{3}+\frac{1}{3}=\frac{2}{3}</math>
<br>
:Thus:
<br>
::<math>{{r}_{eq}}=1.5\Omega >1.2\Omega \text{ - System failed}\text{.}</math>
<br>
If two resistors fail open (e.g. #1 and #2), the equivalent resistance is:
<br>
::<math>\frac{1}{{{r}_{eq}}}=\frac{1}{\infty }+\frac{1}{\infty }+\frac{1}{3}=\frac{1}{3}</math>
<br>
:Thus:
<br>
::<math>{{r}_{eq}}=3\Omega >1.2\Omega \text{ - System failed}\text{.}</math>
<br>
If all three resistors fail open:
<br>
::<math>{{r}_{eq}}=\infty >1.2\Omega \text{ - System failed}\text{.}</math>
<br>
Thus, if  <math>{{r}_{1}}</math> ,  <math>{{r}_{2}}</math> ,  <math>{{r}_{3}}</math>,  or any combination of the three fails, the system fails.  Put another way,  <math>{{r}_{1}}</math>  and  <math>{{r}_{2}}</math>  and  <math>{{r}_{3}}</math>  must succeed in order for the system to succeed.
<br>
The RBD is:
[[Image:chp4image24.png|thumb|center|300px|]]
<br>
In this example it can be seen that even though the three components were physically arranged in parallel, their reliability-wise arrangement is in series.


=Example 15=
=Example 15=

Revision as of 02:39, 16 August 2012


Example 15

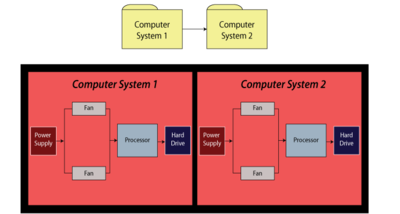
For this example, obtain the reliability equation of the system shown in Figure fig29.

Solution to Example 15

The system reliability equation is:

[math]\displaystyle{ {{R}_{System}}={{R}_{Computer1}}\cdot {{R}_{Computer2}} }[/math]


Now:


[math]\displaystyle{ \begin{align} {{R}_{Computer1}}= & ({{R}_{Power\,Supply}}\cdot {{R}_{Processor}}\cdot {{R}_{HardDrive}} \\ &\cdot(-{{R}_{Fan}}\cdot {{R}_{Fan}}+{{R}_{Fan}}+{{R}_{Fan}})) \end{align} }[/math]


Since the structures of the computer systems are the same, [math]\displaystyle{ {{R}_{Computer1}}={{R}_{Computer2}} }[/math] , then substituting Eqn. (excomp2a) into Eqn. (excomp) yields:

[math]\displaystyle{ \begin{align} {{R}_{System}}= & ({{R}_{Power\,Supply}}\cdot {{R}_{Processor}}) \\ & \cdot {{R}_{HardDrive}}(-R_{Fan}^{2}+2{{R}_{Fan}}){{)}^{2}} \end{align} }[/math]

When using BlockSim to compute the equation, the software will return Eqn. (excomp) for the system and Eqn. (excomp2a) for the subdiagram. Even though BlockSim will make these substitutions internally when performing calculations, it does show them in the System Reliability Equation window.

Illustration of subdiagrams.


BS4.23.png


Example 16

In the diagram shown in Figure Fig32, electricity can flow in both directions. Successful system operation requires at least one output (O1, O2 or O3) to be working.

Create a block diagram for this system.

Solution to Example 16

The bidirectionality of this system can be modeled using mirrored blocks. The diagram is shown in Figure fig33a.

Blocks 5A, 7A and 1A are duplicates (or mirrored blocks) of 5, 7 and 1 respectively.

Example 18

Assume that a system has six failure modes: A, B, C, D, E and F. Furthermore, assume that failure of the entire system will occur if:

• Mode B, C or F occurs.
• Modes A and E, A and D or E and D occur.


Draw the block diagram and obtain the reliability equation.

Solution to Example 18

The diagram is shown in Figure fig35

The reliability equation, as obtained from BlockSim is:

[math]\displaystyle{ \begin{align} {{R}_{System}}= & (-2{{R}_{A}}\cdot {{R}_{B}}\cdot {{R}_{C}}\cdot {{R}_{D}}\cdot {{R}_{2/3}}\cdot {{R}_{E}}\cdot {{R}_{F}} \\ & +{{R}_{A}}\cdot {{R}_{B}}\cdot {{R}_{C}}\cdot {{R}_{D}}\cdot {{R}_{2/3}}\cdot {{R}_{F}} \\ & +{{R}_{A}}\cdot {{R}_{B}}\cdot {{R}_{C}}\cdot {{R}_{2/3}}\cdot {{R}_{E}}\cdot {{R}_{F}} \\ & +{{R}_{B}}\cdot {{R}_{C}}\cdot {{R}_{D}}\cdot {{R}_{2/3}}\cdot {{R}_{E}}\cdot {{R}_{F}}) \end{align} }[/math]


The BlockSim equation includes the node reliability term [math]\displaystyle{ {{R}_{2/3}}, }[/math] which cannot fail, or [math]\displaystyle{ {{R}_{2/3}}=1 }[/math] . This can be removed, yielding:


[math]\displaystyle{ \begin{align} {{R}_{System}}= & (-2{{R}_{A}}\cdot {{R}_{B}}\cdot {{R}_{C}}\cdot {{R}_{D}}\cdot {{R}_{E}}\cdot {{R}_{F}} \\ & +{{R}_{A}}\cdot {{R}_{B}}\cdot {{R}_{C}}\cdot {{R}_{D}}\cdot {{R}_{F}} \\ & +{{R}_{A}}\cdot {{R}_{B}}\cdot {{R}_{C}}\cdot {{R}_{E}}\cdot {{R}_{F}} \\ & +{{R}_{B}}\cdot {{R}_{C}}\cdot {{R}_{D}}\cdot {{R}_{E}}\cdot {{R}_{F}}) \end{align} }[/math]


Retrieved from "https://www.reliawiki.com/index.php?title=BlockSim_Analytical_Examples&oldid=32194"