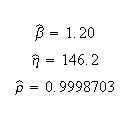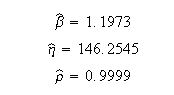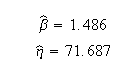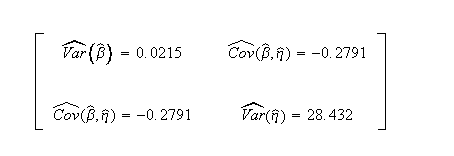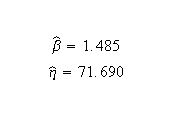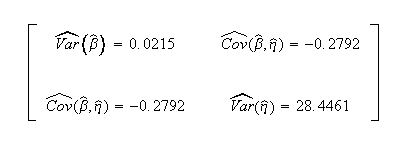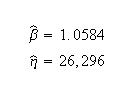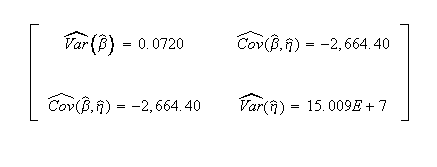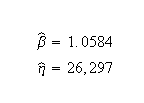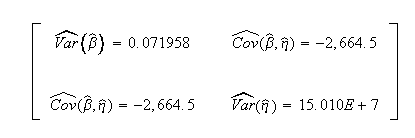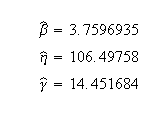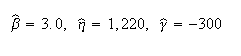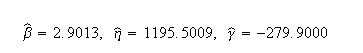Weibull Distribution Examples: Difference between revisions
Chris Kahn (talk | contribs) No edit summary |
Chris Kahn (talk | contribs) |
||
| Line 4: | Line 4: | ||
===Median Rank Plot Example=== | ===Median Rank Plot Example=== | ||
In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of | In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of 10 (as in the data for the next example). This example will use Weibull++'s Quick Statistical Reference (QSR) tool to show how the points in the plot of the following example are calculated. | ||
'''Solution''' | '''Solution''' | ||
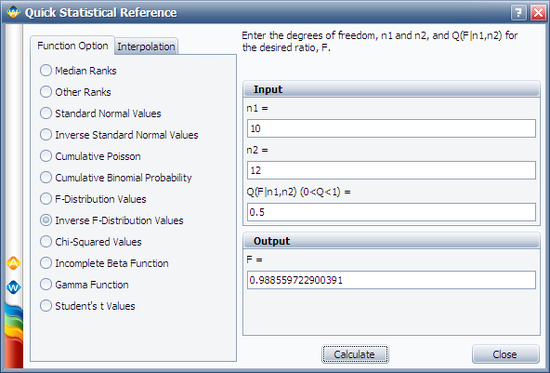
First, open the Quick Statistical Reference and select the '''Inverse F-Distribution Values''' option. | First, open the Quick Statistical Reference tool and select the '''Inverse F-Distribution Values''' option. | ||
In this example, N = 10, j = 6, m = 2(10 - 6 + 1) = 10, and n = 2 x 6 = 12. | In this example, N = 10, j = 6, m = 2(10 - 6 + 1) = 10, and n = 2 x 6 = 12. | ||
| Line 26: | Line 26: | ||
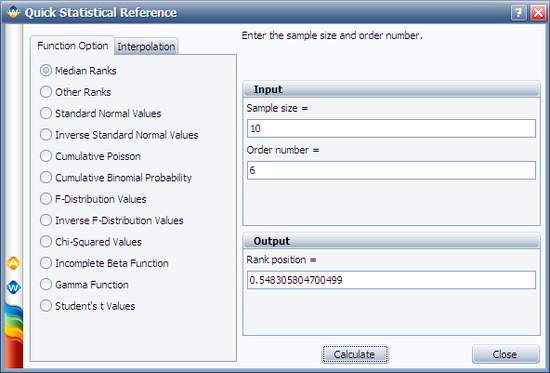
Another method is to use the '''Median Ranks''' option directly, which yields MR(%) = 54.8305%, as shown next: | Another method is to use the '''Median Ranks''' option directly, which yields MR(%) = 54.8305%, as shown next: | ||
[[Image: MR.png|center|550px]] | [[Image: MR.png|center|550px]] | ||
===Published 2P Weibull Distribution Complete Data RRY Example=== | ===Published 2P Weibull Distribution Complete Data RRY Example=== | ||
Revision as of 02:33, 14 August 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
These examples also appear in the Life Data Analysis Reference book.
Median Rank Plot Example
In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of 10 (as in the data for the next example). This example will use Weibull++'s Quick Statistical Reference (QSR) tool to show how the points in the plot of the following example are calculated.
Solution
First, open the Quick Statistical Reference tool and select the Inverse F-Distribution Values option.
In this example, N = 10, j = 6, m = 2(10 - 6 + 1) = 10, and n = 2 x 6 = 12.
Thus, from the F-distribution rank equation:
- [math]\displaystyle{ MR=\frac{1}{1+\left( \frac{10-6+1}{6} \right){{F}_{0.5;10;12}}} }[/math]
Use the QSR to calculate the value of F0.50;10;12 = 0.9886, as shown next:
Consequently:
- [math]\displaystyle{ MR=\frac{1}{1+\left( \frac{5}{6} \right)\times 0.9886}=0.5483=54.83% }[/math]
Another method is to use the Median Ranks option directly, which yields MR(%) = 54.8305%, as shown next:
Published 2P Weibull Distribution Complete Data RRY Example
From Dimitri Kececioglu, Reliability & Life Testing Handbook, Page 418 [20].
Sample of 10 units, all tested to failure. The times-to-failure were recorded at 16; 34; 53; 75; 93; 120; 150; 191; 240; and 339 hours.
Published Results
Published Results (using Rank Regression on Y):
Computed Results in Weibull++
This same data set can be entered into Weibull++ by selecting the Times to Failure type. Use RRY for the estimation method.
Weibull++ computed parameters for RRY are:
The small difference between the published results and the ones obtained from Weibull++ is due to the difference in the median rank values between the two (in the publication, median ranks are obtained from tables to 3 decimal places, whereas in Weibull++ they are calculated and carried out up to the 15th decimal point).
You will also notice that in the examples that follow, a small difference may exist between the published results and the ones obtained from Weibull++. This can be attributed to the difference between the computer numerical precision employed by Weibull++ and the lower number of significant digits used by the original authors. In most of these publications, no information was given as to the numerical precision used.
Published 2P Weibull Distribution Interval Data MLE Example
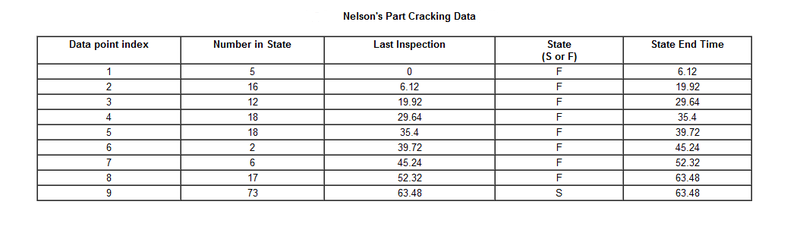
From Wayne Nelson, Applied Life Data Analysis, Page 415 [30]. One hundred and sixty-seven (167) identical parts were inspected for cracks. The following is a table of their last inspection times and times-to-failure:
Published Results:
Published results (using MLE):
Published 95% FM confidence limits on the parameters:
Published variance/covariance matrix:
Computed Results in Weibull++
This same data set can be entered into Weibull++ by selecting the data sheet Times to Failure, with Right Censored Data (Suspensions), with Interval and Left Censored Data and with Grouped Observations options, and using MLE.
Weibull++ computed parameters for maximum likelihood are:
Weibull++ computed 95% FM confidence limits on the parameters:
Weibull++ computed/variance covariance matrix:
Published 2P Weibull Distribution Suspension Data MLE Example
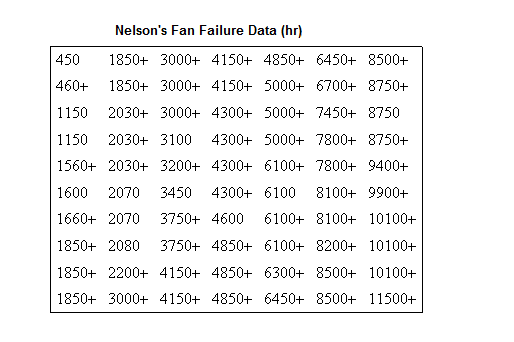
From Wayne Nelson, Fan Example, Applied Life Data Analysis, page 317 [30].
Seventy diesel engine fans accumulated 344,440 hours in service and twelve of them failed. A table of their life data is shown next (+ denotes non-failed units or suspensions, using Dr. Nelson's nomenclature). Evaluate the parameters with their two-sided 95% confidence bounds, using MLE for the two-parameter Weibull distribution.
Published Results:
Weibull parameters (2P-Weibull, MLE):
Published 95% FM confidence limits on the parameters:
Published variance/covariance matrix:
Note that Nelson expresses the results as multiples of 1000 (or = 26.297, etc.). The published results were adjusted by this factor to correlate with Weibull++ results.
Computed Results in Weibull++
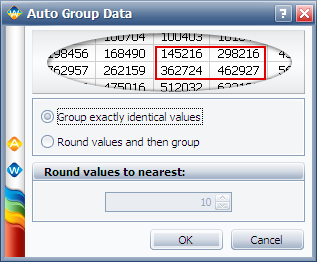
This same data set can be entered into Weibull++ by selecting the data sheet Times to Failure, with Right Censored Data (Suspensions) and I want to enter data in groups (in order to group identical values) options, and using two-parameter Weibull and MLE to calculate the parameter estimates.
You can also enter the data as given in Table without grouping them by opening a Data Sheet with Times to Failure and the with Right Censored Data (Suspensions) options. Then click the Group Data icon and chose Group exactly identical values.
The data will be automatically grouped and put into a new grouped data sheet.
Weibull++ computed parameters for maximum likelihood are:
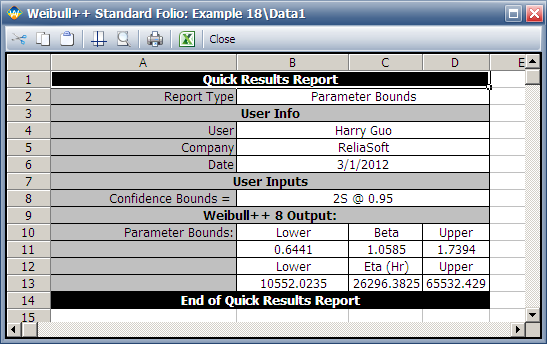
Weibull++ computed 95% FM confidence limits on the parameters:
Weibull++ computed/variance covariance matrix:
The two-sided 95% bounds on the parameters can be determined from the QCP, in the Parameter Bounds tab.
Published 3P Weibull Distribution Grouped Suspension Data MLE Example
From Dallas R. Wingo, IEEE Transactions on Reliability Vol. R-22, No 2, June 1973, Pages 96-100.
Wingo uses the following times-to-failure: 37, 55, 64, 72, 74, 87, 88, 89, 91, 92, 94, 95, 97, 98, 100, 101, 102, 102, 105, 105, 107, 113, 117, 120, 120, 120, 122, 124, 126, 130, 135, 138, 182. In addition, the following suspensions are used: 4 at 70, 5 at 80, 4 at 99, 3 at 121 and 1 at 150.
Published Results (using MLE)
Computed Results in Weibull++
Note that you must have the Use True 3-P MLE on Weibull option in the Weibull++ User Setup selected to replicate these results.
Published 3P Weibull Distribution Probability Plot Example
From Dimitri Kececioglu, Reliability & Life Testing Handbook, Page 406. [20].
Estimate the parameters for three-parameter Weibull, for a sample of ten units all tested to failure. The times-to-failure were recorded at 200; 370; 500; 620; 730; 840; 950; 1,050; 1,160; and 1,400 hours.
Published Results:
Published results (using probability plotting):
Computed Results in Weibull++
Weibull++ computed parameters for rank regression on X are:
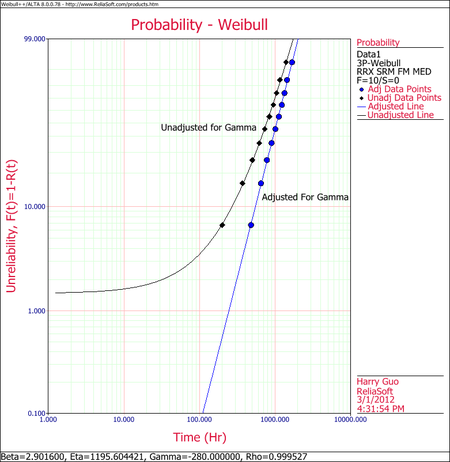
The small difference between the published results and the ones obtained from Weibull++ are due to the difference in the estimation method. In the publication the parameters were estimated using probability plotting (i.e. the fitted line was "eye-balled"). In Weibull++, the parameters were estimated using non-linear regression (a more accurate, mathematically fitted line). Note that γ in this example is negative. This means that the unadjusted for γ line is concave up, as shown next.
Weibull Distribution Conditional Reliability RRX Example
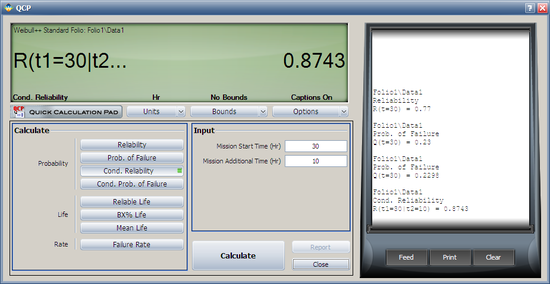
What is the reliability for a new mission of t = 10 hours duration, starting the new mission at the age of T = 30 hours, for the same data as Example 8?
Solution
The conditional reliability is given by:
- [math]\displaystyle{ R(t|T)=\frac{R(T+t)}{R(T)} }[/math]
or:
- [math]\displaystyle{ \hat{R}(10hr|30hr)=\frac{\hat{R}(10+30)}{\hat{R}(30)}=\frac{\hat{R}(40)}{\hat{R}(30)} }[/math]
Again, the Quick Calculation Pad can provide this result directly and more accurately than the plot.
Weibull Disribution Unreliability RRX Example
Assume that six identical units are being tested. All the six failur times are: 93, 34, 16, 120, 53 and 75. What is the unreliability of the units for a mission duration of 30 hours, starting the mission at age zero? To replicate the results in this reference with Weibull++, choose RRX (Rank Regression on X) as the calculation method.
Solution
First, use Weibull++ to obtain the parameters using RRX.
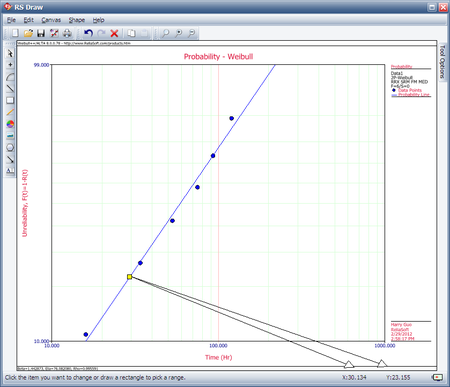
Then, we investigate several methods of solution for this problem. The first, and more laborious, method is to extract the information directly from the plot. You may do this with either the screen plot in RS Draw or the printed copy of the plot. (When extracting information from the screen plot in RS Draw, note that the translated axis position of your mouse is always shown on the bottom right corner.)
Using this first method, enter either the screen plot or the printed plot with T = 30 hours, go up vertically to the straight line fitted to the data, then go horizontally to the ordinate, and read off . Then, a good estimate of the sought unreliability is 23%. (Also, the reliability estimate is 1.0 - 0.23 = 0.77 or 77%.)
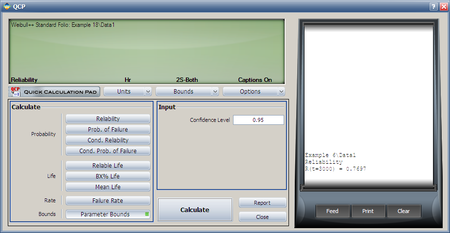
The second method involves the use of the Quick Calculation Pad (QCP).
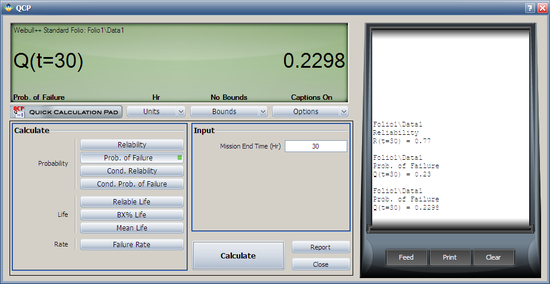
Select Prob. of Failure calculation option and enter 30 hours in the Mission End Time box. Click Calculate to get the result.
Note that the results in QCP vary according to the parameter estimation method used. The above results are obtained using RRX.
Weibull Distribution Complete Data Example
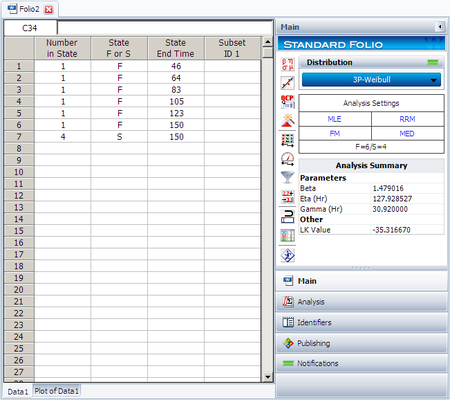
Assume that ten identical units (N = 10) are being reliability tested at the same application and operation stress levels. Six of these units fail during this test after operating the following numbers of hours, [math]\displaystyle{ {T}_{j} }[/math]: 150, 105, 83, 123, 64 and 46. The test is stopped at the sixth failure. Find the parameters of the Weibull pdf that represents these data.
Solution
Open a new Data Folio choosing Times-to-failure data, My data set contains suspensions (right censored data) and I want to enter data in groups.
Enter the data in the appropriate columns. Note that there are four suspensions, as only six of the ten units were tested to failure (the next figure shows the data as entered). Use the three-parameter Weibull and MLE for the calculations.
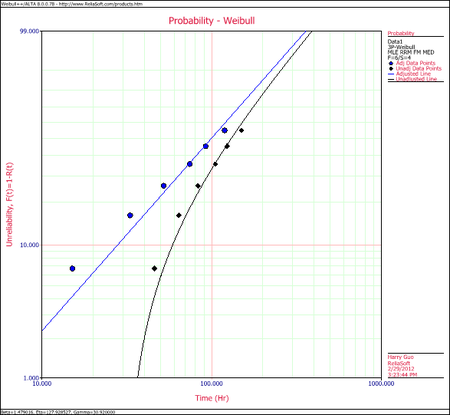
Plot the data.
Note that the original data points, on the curved line, were adjusted by subtracting 30.92 hours to yield a straight line as shown above.
Weibull Distribution Interval Data Example
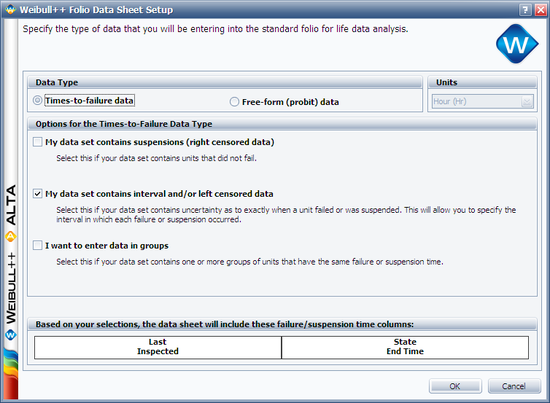
Suppose that we have run an experiment with eight units being tested and the following is a table of their last inspection times and times-to-failure:
| Data Point Index | Last Inspection | Time to Failure |
| 1 | 30 | 32 |
| 2 | 32 | 35 |
| 3 | 35 | 37 |
| 4 | 37 | 40 |
| 5 | 42 | 42 |
| 6 | 45 | 45 |
| 7 | 50 | 50 |
| 8 | 55 | 55 |
Analyze the data using several different parameter estimation techniques and compare the results.
Solution
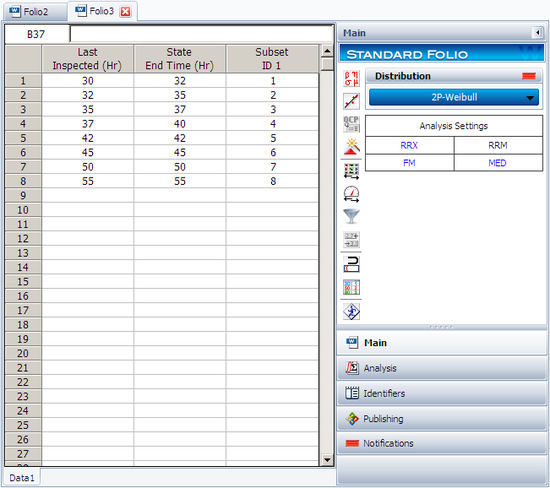
This data set can be entered into Weibull++ by opening a new Data Folio and choosing Times-to-failure and My data set contains interval and/or left censored data.
The data is entered as follows,
The computed parameters using maximum likelihood are:
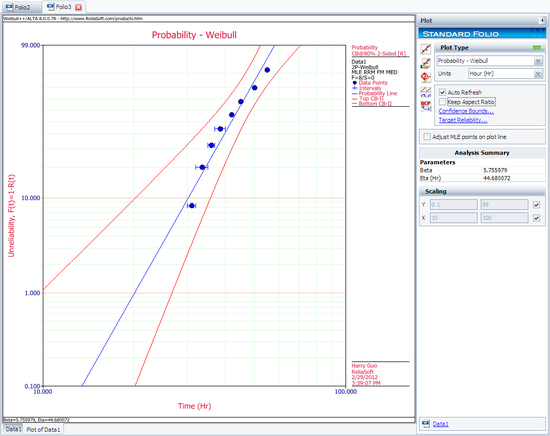
- [math]\displaystyle{ \begin{align} & \hat{\beta }=5.76 \\ & \hat{\eta }=44.68 \\ \end{align} }[/math]
using RRX or rank regression on X:
- [math]\displaystyle{ \begin{align} & \hat{\beta }=5.70 \\ & \hat{\eta }=44.54 \\ \end{align} }[/math]
and using RRY or rank regression on Y:
- [math]\displaystyle{ \begin{align} & \hat{\beta }=5.41 \\ & \hat{\eta }=44.76 \\ \end{align} }[/math]
The plot of the MLE solution with the two-sided 90% confidence bounds is:
Weibull Distribution Reliable Life RRX Example
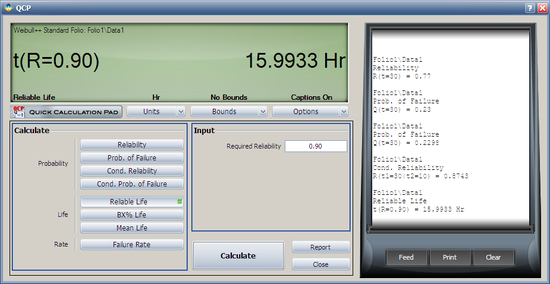
For the data in Example 8 and 9, what is the longest mission that this equipment should undertake for a reliability of 90%?
Solution
Using the QCP again, choose Reliable Life and enter the Required Reliability, 0.90, and click Calculate. The result is 15.9933 hours.
Weibull Distribution Suspension Data Example
ACME company manufactures widgets, and is currently engaged in reliability testing a new widget design. Nineteen units are being reliability tested, but due to the tremendous demand for widgets, units are removed from the test whenever the production cannot cover the demand. The test is terminated at the 67th day when the last widget is removed from the test. The following Table contains the collected data.
| Data Point Index | State (F/S) | Time to Failure |
| 1 | F | 2 |
| 2 | S | 3 |
| 3 | F | 5 |
| 4 | S | 7 |
| 5 | F | 11 |
| 6 | S | 13 |
| 7 | S | 17 |
| 8 | S | 19 |
| 9 | F | 23 |
| 10 | F | 29 |
| 11 | S | 31 |
| 12 | F | 37 |
| 13 | S | 41 |
| 14 | F | 43 |
| 15 | S | 47 |
| 16 | S | 53 |
| 17 | F | 59 |
| 18 | S | 61 |
| 19 | S | 67 |
Solution
In this example, we see that the number of failures is less than the number of suspensions. This is a very common situation, since reliability tests are often terminated before all units fail due to financial or time constraints. Further, some suspensions will be recorded when a failure occurs that is not due to a legitimate failure mode, such as operator error. In cases such as this, a suspension is recorded, since the unit under test cannot be said to have had a legitimate failure.
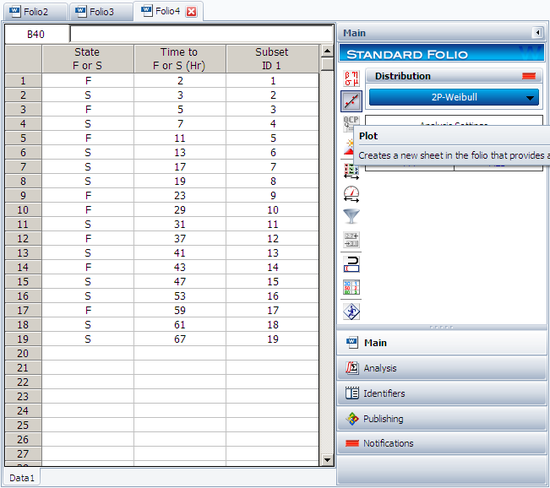
This data set can be entered into Weibull++ using Times-to-failure and My data set contains suspensions (right censored data).
After enter the data, the data folio looks like:
We will use the two-parameter Weibull to solve this problem. The parameters using maximum likelihood are:
- [math]\displaystyle{ \begin{align} & \hat{\beta }=1.145 \\ & \hat{\eta }=65.97 \\ \end{align} }[/math]
using RRX:
- [math]\displaystyle{ \begin{align} & \hat{\beta }=0.914\\ & \hat{\eta }=79.38 \\ \end{align} }[/math]
and using RRY:
- [math]\displaystyle{ \begin{align} & \hat{\beta }=0.895\\ & \hat{\eta }=82.02 \\ \end{align} }[/math]
Published 3P Weibull Distribution Probability Plot Example
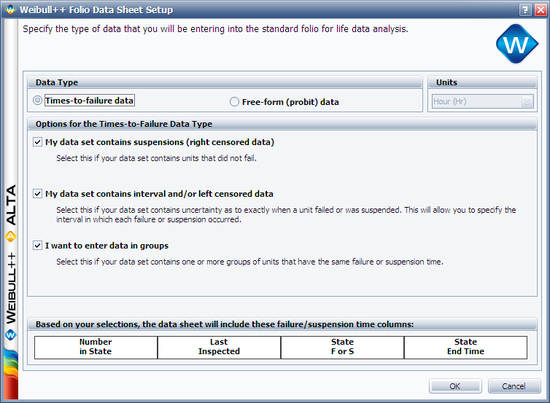
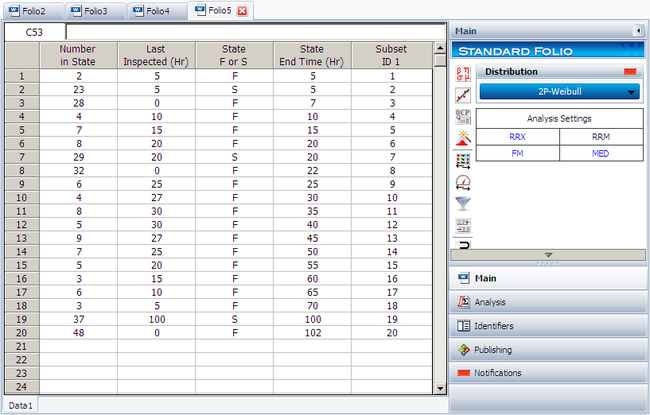
Suppose we want to model a left censored, right censored, interval, and complete data set, consisting of 274 units under test of which 185 units fail. The following Table contains the data.
| Data Point Index | Number in State | Last Inspection | State (S or F) | State End Time |
| 1 | 2 | 5 | F | 5 |
| 2 | 23 | 5 | S | 5 |
| 3 | 28 | 0 | F | 7 |
| 4 | 4 | 10 | F | 10 |
| 5 | 7 | 15 | F | 15 |
| 6 | 8 | 20 | F | 20 |
| 7 | 29 | 20 | S | 20 |
| 8 | 32 | 0 | F | 22 |
| 9 | 6 | 25 | F | 25 |
| 10 | 4 | 27 | F | 30 |
| 11 | 8 | 30 | F | 35 |
| 12 | 5 | 30 | F | 40 |
| 13 | 9 | 27 | F | 45 |
| 14 | 7 | 25 | F | 50 |
| 15 | 5 | 20 | F | 55 |
| 16 | 3 | 15 | F | 60 |
| 17 | 6 | 10 | F | 65 |
| 18 | 3 | 5 | F | 70 |
| 19 | 37 | 100 | S | 100 |
| 20 | 48 | 0 | F | 102 |
Solution
This data set can be entered into Weibull++ by selecting the Times-to-failure and My data set contains suspensions (right censored data), My data set contains interval and/or left censored data and I want to enter data in groups options.
Since standard ranking methods for dealing with these different data types are inadequate, we will want to use the ReliaSoft ranking method. This option is the default in Weibull++ when dealing with interval data. The Data Folio is given below:
The computed parameters using MLE are:
- [math]\displaystyle{ \hat{\beta }=0.748;\text{ }\hat{\eta }=44.38 }[/math]
using RRX:
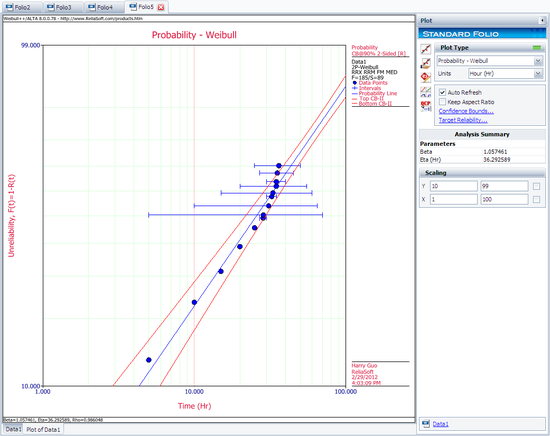
- [math]\displaystyle{ \hat{\beta }=1.057;\text{ }\hat{\eta }=36.29 }[/math]
and using RRY:
- [math]\displaystyle{ \hat{\beta }=0.998;\text{ }\hat{\eta }=37.16 }[/math]
The plot with the two-sided 90% confidence bounds for the rank regression on X solution is: