Template:Example: Median Rank Plot Example: Difference between revisions
No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
'''Median Rank Plot Example''' | '''Median Rank Plot Example''' | ||
In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of ten. This will be used to illustrate two of the built-in functions in Weibull++'s | In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of ten. This will be used to illustrate two of the built-in functions in Weibull++'s Quick Statistical Reference. | ||
'''Solution''' | '''Solution''' | ||
First, open the Quick Statistical Reference | First, open the Quick Statistical Reference and select the '''Inverse F-Distribution Values''' option. | ||
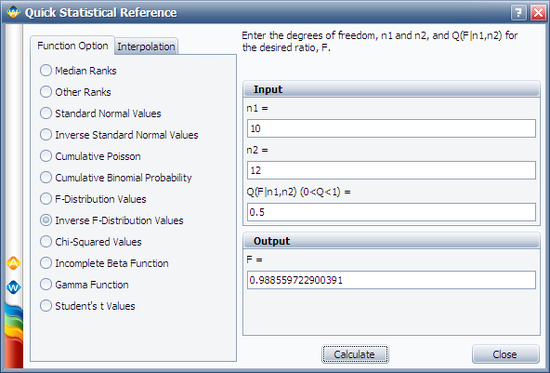
In this example, N = 10, j = 6, m = 2(10 - 6 + 1) = 10, and n = 2 x 6 = 12. | |||
In this example N = 10, j = 6, m = 2(10 - 6 + 1) = 10, and n = 2 x 6 = 12. | |||
Thus, from the F-distribution rank equation: | Thus, from the F-distribution rank equation: | ||
Revision as of 09:27, 8 August 2012
Median Rank Plot Example
In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of ten. This will be used to illustrate two of the built-in functions in Weibull++'s Quick Statistical Reference.
Solution
First, open the Quick Statistical Reference and select the Inverse F-Distribution Values option.
In this example, N = 10, j = 6, m = 2(10 - 6 + 1) = 10, and n = 2 x 6 = 12.
Thus, from the F-distribution rank equation:
- [math]\displaystyle{ MR=\frac{1}{1+\left( \frac{10-6+1}{6} \right){{F}_{0.5;10;12}}} }[/math]
Calculate the value of F0.50:10:12 by using the Inverse F-Distribution Values option from the Quick Statistical Reference, or F0.50;10;12 = 0.9886 as shown next:
Consequently:
- [math]\displaystyle{ MR=\frac{1}{1+\left( \frac{5}{6} \right)\times 0.9886}=0.5483=54.83% }[/math]
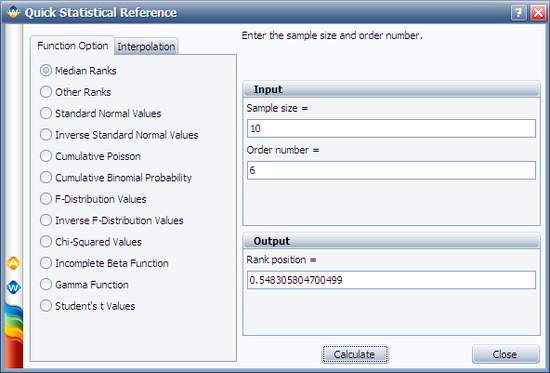
Another method is to use the Median Ranks option directly, which yields MR(%) = 54.8305%, as shown next: