Same Example Modeled with RBDs or Fault Trees: Difference between revisions
Lisa Hacker (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 6: | Line 6: | ||
===Problem Statement=== | ===Problem Statement=== | ||
Assume that a component can fail due to six independent primary failure modes: A , B , C , D , E and F . Some of these primary modes can be broken down further into the events that can cause them, or sub-modes. Furthermore, assume that once a mode occurs, the event also occurs and the mode does not go away. Specifically: | Assume that a component can fail due to six independent primary failure modes: A, B, C, D, E and F. Some of these primary modes can be broken down further into the events that can cause them, or sub-modes. Furthermore, assume that once a mode occurs, the event also occurs and the mode does not go away. Specifically: | ||
<br> | <br> | ||
*The component fails if mode A , B or C occurs. | *The component fails if mode A, B or C occurs. | ||
*If mode D , E or F occurs alone, the component does not fail; however, the component will fail if any two (or more) of these modes occur (i.e., D and E ; D and F ; E and F ). | *If mode D, E or F occurs alone, the component does not fail; however, the component will fail if any two (or more) of these modes occur (i.e., D and E ; D and F ; E and F). | ||
*Modes D , E and F have a constant rate of occurrence (exponential distribution) with mean times of occurrence of | *Modes D, E and F have a constant rate of occurrence (exponential distribution) with mean times of occurrence of 200,000, 175,000 and 500,000 hours, respectively. | ||
*The rates of occurrence for modes A , B and C depend on their sub-modes. | *The rates of occurrence for modes A, B and C depend on their sub-modes. | ||
Do the following: | Do the following: | ||
#Determine the reliability of the component after 1 year ( | #Determine the reliability of the component after 1 year (8,760 hours). | ||
#Determine the B10 life of the component. | #Determine the B10 life of the component. | ||
#Determine the mean time to failure ( | #Determine the mean time to failure (MTTF) of the component. | ||
#Rank the modes in order of importance at 1 year. | #Rank the modes in order of importance at 1 year. | ||
#Recalculate results 1, 2 and 3 assuming mode B is eliminated. | #Recalculate results 1, 2 and 3 assuming mode B is eliminated. | ||
To begin the analysis, modes A , B and C can be broken down further based on specific events (sub-modes), as defined next. | To begin the analysis, modes A, B and C can be broken down further based on specific events (sub-modes), as defined next. | ||
===Mode A=== | ===Mode A=== | ||
There are five independent events (sub-modes) associated with mode A : events | There are five independent events (sub-modes) associated with mode A : events S1, S2, T1, T2 and Y. It is assumed that events S1 and S2 each have a constant rate of occurrence with a probability of occurrence in a single year (<math>8760</math> hours) of <math>1</math> in <math>10,000</math> and <math>1</math> in <math>20,000</math>, respectively. Events T1 and T2 are more likely to occur in an older component than a newer one (i.e., they have an increasing rate of occurrence) and have a probability of occurrence of <math>1</math> in <math>10,000</math> and <math>1</math> in <math>20,000</math>, respectively, in a single year and <math>1</math> in <math>1,000</math> and <math>1</math> in <math>3,000</math>, respectively, after two years. Event Y also has a constant rate of occurrence with a probability of occurrence of <math>1</math> in <math>1,000</math> in a single year. There are three possible ways for mode A to manifest itself: | ||
#Events | #Events S1 and S2 both occur. | ||
#Event | #Event T1 or T2 occurs. | ||
#Event | #Event Y and either event S1 or event S2 occur (i.e., events Y and S1 or events Y and S2 occur). | ||
'''RBD Solution for Mode A''' | '''RBD Solution for Mode A''' | ||
| Line 37: | Line 37: | ||
[[Image:6.png|center|400px|Reliability block diagram for mode A.]] | [[Image:6.png|center|400px|Reliability block diagram for mode A.]] | ||
Each mode is identified in the RBD. Furthermore, two additional items are included: a starting block ( | Each mode is identified in the RBD. Furthermore, two additional items are included: a starting block (NF) and an end node (2/2). The starting block and the end node are set so they cannot fail and, therefore, will not affect the results. The end node is used to define a 2-out-of-2 configuration (i.e., both paths leading into the node must work). | ||
'''Fault Tree Solution for Mode A''' | '''Fault Tree Solution for Mode A''' | ||
| Line 45: | Line 45: | ||
[[Image:7.png|center|400px|Fault tree for mode ''A''.]] | [[Image:7.png|center|400px|Fault tree for mode ''A''.]] | ||
Each mode is identified as an event in the fault tree. The following figure shows an alternative representation for mode A using [[Fault_Tree_Diagrams_and_System_Analysis#Using_Mirrored_Blocks_to_Represent_Complex_RBDs_as_FTDs|mirrored events]] for | Each mode is identified as an event in the fault tree. The following figure shows an alternative representation for mode A using [[Fault_Tree_Diagrams_and_System_Analysis#Using_Mirrored_Blocks_to_Represent_Complex_RBDs_as_FTDs|mirrored events]] for S1 and S2. | ||
[[Image:8.png|center|400px|An alternative representation of the fault tree for mode ''A'' using mirrored events.]] | [[Image:8.png|center|400px|An alternative representation of the fault tree for mode ''A'' using mirrored events.]] | ||
| Line 60: | Line 60: | ||
\end{align}</math> | \end{align}</math> | ||
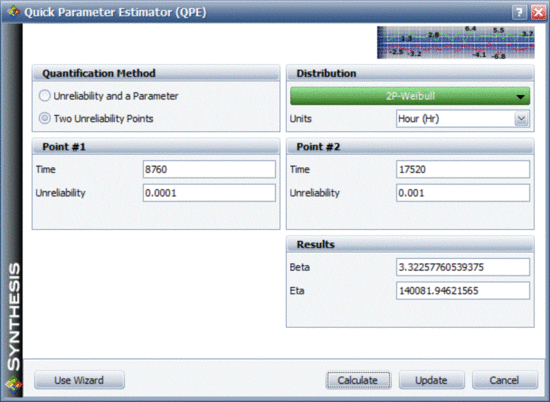
Based on the given probabilities, distribution parameters are computed for each block (either RBD block or the fault tree event block). One way is to compute them using the Parameter Experimenter, as shown in the figure below. In this figure and for | Based on the given probabilities, distribution parameters are computed for each block (either RBD block or the fault tree event block). One way is to compute them using the Parameter Experimenter, as shown in the figure below. In this figure and for S1, the probability is 1 in 10,000 in one year (8,760 hours), thus the exponential failure rate is 1.1416e-8. This can be repeated for S2 and Y. | ||
[[Image:10.26.gif|center|550px|BlockSim's Parameter Experimenter.]] | [[Image:10.26.gif|center|550px|BlockSim's Parameter Experimenter.]] | ||
Events | Events T1 and T2 need to be modeled using a life distribution that does not have a constant failure rate. Using BlockSim's Parameter Experimenter and selecting the Weibull distribution, the parameter values for events T1 and T2 are shown in the figures below. | ||
[[Image:10.27.gif|center|550px|Parameter values for event ''T''1.]] | [[Image:10.27.gif|center|550px|Parameter values for event ''T''1.]] | ||
| Line 71: | Line 71: | ||
===Mode B=== | ===Mode B=== | ||
There are three dependent events associated with mode B : events | There are three dependent events associated with mode B : events BA, BB and BC. | ||
:• Two out of the three events must occur for mode B to occur. | :• Two out of the three events must occur for mode B to occur. | ||
::o Events | ::o Events BA, BB and BC all have an exponential distribution with a mean of 50,000 hours. | ||
::o The events are dependent (i.e., if | ::o The events are dependent (i.e., if BA, BB or BC occurs, then the remaining events are more likely to occur). Specifically, when one event occurs, the MTTF of the remaining events is halved. | ||
This is basically a load sharing configuration. The reliability function for each block will change depending on the other events. Therefore, the reliability of each block is not only dependent on time, but also on the stress (load) that the block experiences. | This is basically a load sharing configuration. The reliability function for each block will change depending on the other events. Therefore, the reliability of each block is not only dependent on time, but also on the stress (load) that the block experiences. | ||
| Line 96: | Line 96: | ||
===Mode C=== | ===Mode C=== | ||
There are two sequential events associated with mode C : | There are two sequential events associated with mode C : CA and CB. | ||
:• Both events must occur for mode C to occur. | :• Both events must occur for mode C to occur. | ||
:• Event | :• Event CB will only occur if event CA has occurred. | ||
:• If event | :• If event CA has not occurred, then event CB will not occur. | ||
:• Events | :• Events CA and CB both occur based on a Weibull distribution. | ||
:• For event | :• For event CA, <math>\beta </math> =2 and <math>\eta </math> =30,000 hours. | ||
:• For event | :• For event CB, <math>\beta </math> =2 and <math>\eta </math> =10,000 hours. | ||
'''RBD Solution for Mode C''' | '''RBD Solution for Mode C''' | ||
To model this, you can think of a scenario similar to standby redundancy. Basically, if | To model this, you can think of a scenario similar to standby redundancy. Basically, if CA occurs then CB gets initiated. A Standby container can be used to model this, as shown in the figure below. | ||
[[Image:10.32.png|center|150px|Standby container for mode C.]] | [[Image:10.32.png|center|150px|Standby container for mode C.]] | ||
In this case, event | In this case, event CA is set as the active component and CB as the standby. If event CA occurs, CB will be initiated. For this analysis, a perfect switch is assumed. The properties are set in BlockSim as follows: | ||
Contained Items | Contained Items | ||
:• | :• CA : Active failure distribution, Weibull distribution (<math>\beta </math> =2, <math>\eta </math> =30,000). | ||
:• | :• CA : Quiescent failure distribution: None, cannot fail or age in this mode. | ||
:• | :• CB : Active failure distribution, Weibull distribution (<math>\beta </math> =2, <math>\eta </math> =10,000). | ||
:• | :• CB : Quiescent failure distribution: None, cannot fail or age in this mode. | ||
Switch | Switch | ||
| Line 134: | Line 134: | ||
'''Mode C Discussion''' | '''Mode C Discussion''' | ||
The failure distribution settings for event | The failure distribution settings for event CA are shown in the figure below. | ||
[[Image:10.34.gif|center|550px|Failure distribution settings for event ''C'' ''A''.]] | [[Image:10.34.gif|center|550px|Failure distribution settings for event ''C'' ''A''.]] | ||
The failure distribution properties for event | The failure distribution properties for event CB are set in the same manner. | ||
===Modes D, E and F=== | ===Modes D, E and F=== | ||
Modes D , E and F can all be represented using the exponential distribution. The failure distribution properties for modes D , E and F are: | Modes D, E and F can all be represented using the exponential distribution. The failure distribution properties for modes D, E and F are: | ||
:• D : | :• D : MTTF = 200,000 hours. | ||
:• E : | :• E : MTTF = 175,000 hours. | ||
:• F : | :• F : MTTF = 500,000 hours. | ||
===The Entire Component=== | ===The Entire Component=== | ||
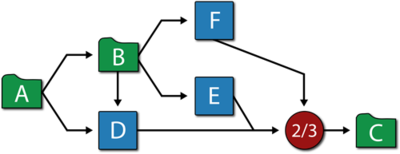
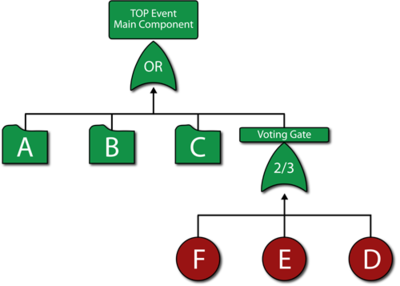
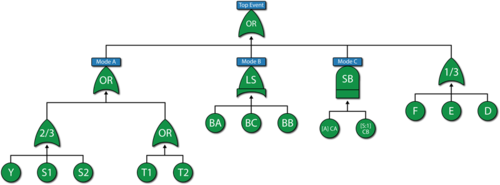
The last step is to set up the model for the component based on the primary modes ( A , B , C , D , E and F ). Modes A , B and C can each be represented by single blocks that encapsulate the subdiagrams already created. The RBD in the first figure below represents the primary failure modes for the component while the fault tree in second figure below illustrates the same. The node represented by 2/3 in the RBD indicates a 2-out-of-3 configuration. The Voting OR gate in the fault tree accomplishes the same. Subdiagrams are used in both configurations for the sub-modes. | The last step is to set up the model for the component based on the primary modes (A, B, C, D, E and F). Modes A, B and C can each be represented by single blocks that encapsulate the subdiagrams already created. The RBD in the first figure below represents the primary failure modes for the component while the fault tree in second figure below illustrates the same. The node represented by 2/3 in the RBD indicates a 2-out-of-3 configuration. The Voting OR gate in the fault tree accomplishes the same. Subdiagrams are used in both configurations for the sub-modes. | ||
[[Image:10.35.png|center|400px|RBD of the component.]] | [[Image:10.35.png|center|400px|RBD of the component.]] | ||
| Line 165: | Line 165: | ||
\end{align}</math> | \end{align}</math> | ||
where <math>R{{(t)}_{A}}</math> , <math>R{{(t)}_{B}}</math> and <math>R{{(t)}_{C}}</math> are the reliability equations corresponding to the sub-modes. | where <math>R{{(t)}_{A}}</math>, <math>R{{(t)}_{B}}</math> and <math>R{{(t)}_{C}}</math> are the reliability equations corresponding to the sub-modes. | ||
===Analysis and Discussion=== | ===Analysis and Discussion=== | ||
| Line 171: | Line 171: | ||
The questions posed earlier can be answered using BlockSim. Regardless of the approach used (i.e., RBD or FTA), the answers are the same. | The questions posed earlier can be answered using BlockSim. Regardless of the approach used (i.e., RBD or FTA), the answers are the same. | ||
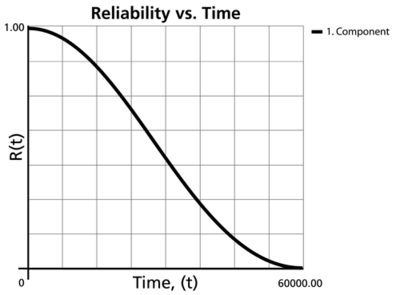
#The reliability of the component at 1 year (8,760 hours) can be calculated using the Analytical Quick Calculation Pad (QCP) or by viewing the reliability vs. time plot, as displayed in the following figure. <math>R(t=8760)=86.4975%</math> . | #The reliability of the component at 1 year (8,760 hours) can be calculated using the Analytical Quick Calculation Pad (QCP) or by viewing the reliability vs. time plot, as displayed in the following figure. <math>R(t=8760)=86.4975%</math>. | ||
[[Image:10_37.png|center|400px|Reliability vs. time plot for the component.]] | [[Image:10_37.png|center|400px|Reliability vs. time plot for the component.]] | ||
#Using the Analytical QCP, the B10 life of the component is estimated to be 7,373.94 hours. | #Using the Analytical QCP, the B10 life of the component is estimated to be 7,373.94 hours. | ||
| Line 180: | Line 180: | ||
:::a) <math>R(t=8760)=98.72%.</math> | :::a) <math>R(t=8760)=98.72%.</math> | ||
:::b) <math>B10</math> = 16,928.38 hours. | :::b) <math>B10</math> = 16,928.38 hours. | ||
:::c) | :::c) MTTF = 34,552.89 hours. | ||
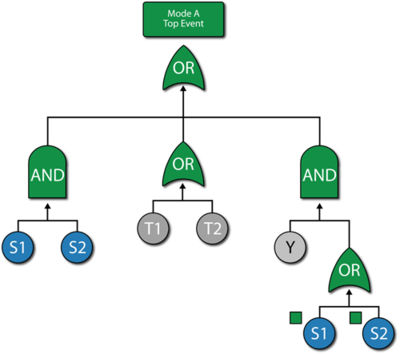
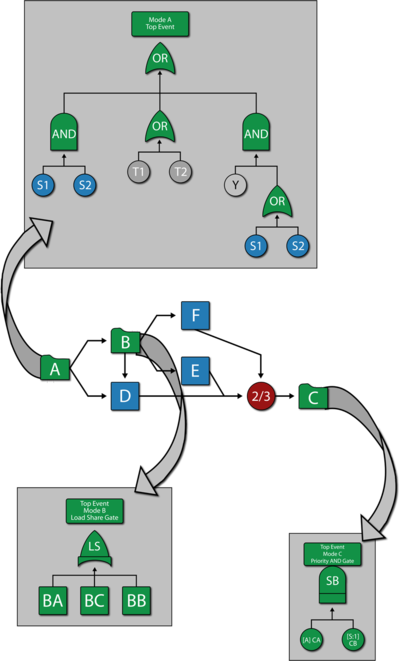
There are multiple options for modeling systems with fault trees and RBDs in BlockSim. The first figure below shows the complete fault tree for the component without using subdiagrams (Transfer gates) while the second figure below illustrates a hybrid analysis utilizing an RBD for the component and fault trees as the subdiagrams. The results are the same regardless of the option chosen. | There are multiple options for modeling systems with fault trees and RBDs in BlockSim. The first figure below shows the complete fault tree for the component without using subdiagrams (Transfer gates) while the second figure below illustrates a hybrid analysis utilizing an RBD for the component and fault trees as the subdiagrams. The results are the same regardless of the option chosen. | ||
Revision as of 06:05, 8 August 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at BlockSim examples and BlockSim reference examples.
This example also appears in the System Analysis Reference book.
This example demonstrates how you can model the same analysis scenario using either RBDs or fault trees in BlockSim. The results will be the same with either approach.
Problem Statement
Assume that a component can fail due to six independent primary failure modes: A, B, C, D, E and F. Some of these primary modes can be broken down further into the events that can cause them, or sub-modes. Furthermore, assume that once a mode occurs, the event also occurs and the mode does not go away. Specifically:
- The component fails if mode A, B or C occurs.
- If mode D, E or F occurs alone, the component does not fail; however, the component will fail if any two (or more) of these modes occur (i.e., D and E ; D and F ; E and F).
- Modes D, E and F have a constant rate of occurrence (exponential distribution) with mean times of occurrence of 200,000, 175,000 and 500,000 hours, respectively.
- The rates of occurrence for modes A, B and C depend on their sub-modes.
Do the following:
- Determine the reliability of the component after 1 year (8,760 hours).
- Determine the B10 life of the component.
- Determine the mean time to failure (MTTF) of the component.
- Rank the modes in order of importance at 1 year.
- Recalculate results 1, 2 and 3 assuming mode B is eliminated.
To begin the analysis, modes A, B and C can be broken down further based on specific events (sub-modes), as defined next.
Mode A
There are five independent events (sub-modes) associated with mode A : events S1, S2, T1, T2 and Y. It is assumed that events S1 and S2 each have a constant rate of occurrence with a probability of occurrence in a single year ([math]\displaystyle{ 8760 }[/math] hours) of [math]\displaystyle{ 1 }[/math] in [math]\displaystyle{ 10,000 }[/math] and [math]\displaystyle{ 1 }[/math] in [math]\displaystyle{ 20,000 }[/math], respectively. Events T1 and T2 are more likely to occur in an older component than a newer one (i.e., they have an increasing rate of occurrence) and have a probability of occurrence of [math]\displaystyle{ 1 }[/math] in [math]\displaystyle{ 10,000 }[/math] and [math]\displaystyle{ 1 }[/math] in [math]\displaystyle{ 20,000 }[/math], respectively, in a single year and [math]\displaystyle{ 1 }[/math] in [math]\displaystyle{ 1,000 }[/math] and [math]\displaystyle{ 1 }[/math] in [math]\displaystyle{ 3,000 }[/math], respectively, after two years. Event Y also has a constant rate of occurrence with a probability of occurrence of [math]\displaystyle{ 1 }[/math] in [math]\displaystyle{ 1,000 }[/math] in a single year. There are three possible ways for mode A to manifest itself:
- Events S1 and S2 both occur.
- Event T1 or T2 occurs.
- Event Y and either event S1 or event S2 occur (i.e., events Y and S1 or events Y and S2 occur).
RBD Solution for Mode A
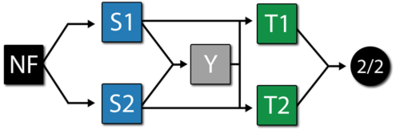
The RBD that satisfies the conditions for mode A is shown in the figure below.
Each mode is identified in the RBD. Furthermore, two additional items are included: a starting block (NF) and an end node (2/2). The starting block and the end node are set so they cannot fail and, therefore, will not affect the results. The end node is used to define a 2-out-of-2 configuration (i.e., both paths leading into the node must work).
Fault Tree Solution for Mode A
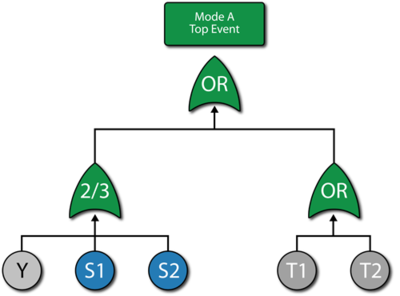
The fault tree for mode A is shown in the figure below.
Each mode is identified as an event in the fault tree. The following figure shows an alternative representation for mode A using mirrored events for S1 and S2.
Mode A Discussion
The system reliability equation for this configuration (regardless of how it is drawn) is:
- [math]\displaystyle{ \begin{align} R(t)= & -2{{R}_{T2}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{S1}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{S2}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{T1}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{Y}} \\ & +{{R}_{T2}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{S1}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{S2}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{T1}} \\ & +{{R}_{T2}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{S1}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{T1}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{Y}} \\ & +{{R}_{T2}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{S2}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{T1}}\text{ }\!\!\cdot\!\!\text{ }{{R}_{Y}} \end{align} }[/math]
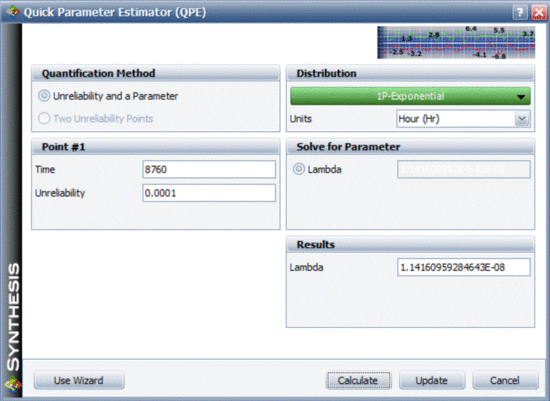
Based on the given probabilities, distribution parameters are computed for each block (either RBD block or the fault tree event block). One way is to compute them using the Parameter Experimenter, as shown in the figure below. In this figure and for S1, the probability is 1 in 10,000 in one year (8,760 hours), thus the exponential failure rate is 1.1416e-8. This can be repeated for S2 and Y.
Events T1 and T2 need to be modeled using a life distribution that does not have a constant failure rate. Using BlockSim's Parameter Experimenter and selecting the Weibull distribution, the parameter values for events T1 and T2 are shown in the figures below.
Mode B
There are three dependent events associated with mode B : events BA, BB and BC.
- • Two out of the three events must occur for mode B to occur.
- o Events BA, BB and BC all have an exponential distribution with a mean of 50,000 hours.
- o The events are dependent (i.e., if BA, BB or BC occurs, then the remaining events are more likely to occur). Specifically, when one event occurs, the MTTF of the remaining events is halved.
This is basically a load sharing configuration. The reliability function for each block will change depending on the other events. Therefore, the reliability of each block is not only dependent on time, but also on the stress (load) that the block experiences.
RBD Solution for Mode B
The reliability block diagram for mode B is shown in the figure below.
Fault Tree Solution for Mode B
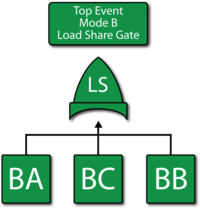
The fault tree for mode B is shown in the figure below. A Load Sharing gate is used.
Mode B Discussion
To describe the dependency, a Load Sharing gate and dependent event blocks are used. Since the failure rate is assumed to be constant, an exponential distribution is used. Furthermore, for simplicity, an Arrhenius life-stress relationship is used with the parameters B=2.0794 and C=6250.
Mode C
There are two sequential events associated with mode C : CA and CB.
- • Both events must occur for mode C to occur.
- • Event CB will only occur if event CA has occurred.
- • If event CA has not occurred, then event CB will not occur.
- • Events CA and CB both occur based on a Weibull distribution.
- • For event CA, [math]\displaystyle{ \beta }[/math] =2 and [math]\displaystyle{ \eta }[/math] =30,000 hours.
- • For event CB, [math]\displaystyle{ \beta }[/math] =2 and [math]\displaystyle{ \eta }[/math] =10,000 hours.
RBD Solution for Mode C
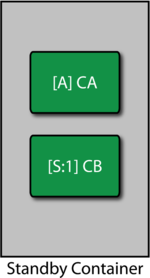
To model this, you can think of a scenario similar to standby redundancy. Basically, if CA occurs then CB gets initiated. A Standby container can be used to model this, as shown in the figure below.
In this case, event CA is set as the active component and CB as the standby. If event CA occurs, CB will be initiated. For this analysis, a perfect switch is assumed. The properties are set in BlockSim as follows:
Contained Items
- • CA : Active failure distribution, Weibull distribution ([math]\displaystyle{ \beta }[/math] =2, [math]\displaystyle{ \eta }[/math] =30,000).
- • CA : Quiescent failure distribution: None, cannot fail or age in this mode.
- • CB : Active failure distribution, Weibull distribution ([math]\displaystyle{ \beta }[/math] =2, [math]\displaystyle{ \eta }[/math] =10,000).
- • CB : Quiescent failure distribution: None, cannot fail or age in this mode.
Switch
- • Active Switching: Always works (100% reliability) and instant switch (no delays).
- • Quiescent Switch failure distribution: None, cannot fail or age in this mode.
Fault Tree Solution for Mode C
The fault tree for mode C is shown in the figure below. Note that the sequence is enforced by the Standby gate (used as a Sequence Enforcing gate).
Mode C Discussion
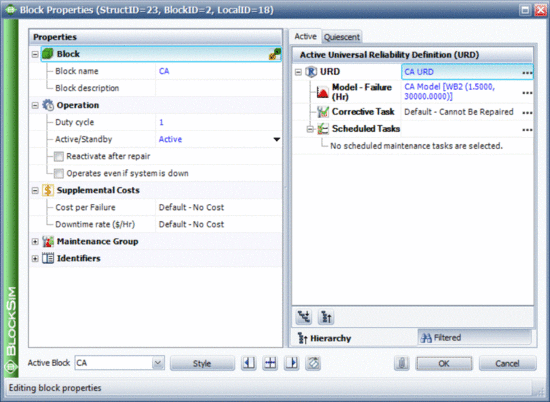
The failure distribution settings for event CA are shown in the figure below.
The failure distribution properties for event CB are set in the same manner.
Modes D, E and F
Modes D, E and F can all be represented using the exponential distribution. The failure distribution properties for modes D, E and F are:
- • D : MTTF = 200,000 hours.
- • E : MTTF = 175,000 hours.
- • F : MTTF = 500,000 hours.
The Entire Component
The last step is to set up the model for the component based on the primary modes (A, B, C, D, E and F). Modes A, B and C can each be represented by single blocks that encapsulate the subdiagrams already created. The RBD in the first figure below represents the primary failure modes for the component while the fault tree in second figure below illustrates the same. The node represented by 2/3 in the RBD indicates a 2-out-of-3 configuration. The Voting OR gate in the fault tree accomplishes the same. Subdiagrams are used in both configurations for the sub-modes.
Once the diagrams have been created, the reliability equation for the system can be obtained, as follows:
- [math]\displaystyle{ \begin{align} R{{(t)}_{System}}= & R{{(t)}_{A}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{B}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{F}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{D}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{C}} \\ & +R{{(t)}_{A}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{B}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{F}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{C}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{E}} \\ & +R{{(t)}_{A}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{B}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{D}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{C}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{E}} \\ & -2(R{{(t)}_{A}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{B}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{F}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{D}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{C}}\text{ }\!\!\cdot\!\!\text{ }R{{(t)}_{E}}) \end{align} }[/math]
where [math]\displaystyle{ R{{(t)}_{A}} }[/math], [math]\displaystyle{ R{{(t)}_{B}} }[/math] and [math]\displaystyle{ R{{(t)}_{C}} }[/math] are the reliability equations corresponding to the sub-modes.
Analysis and Discussion
The questions posed earlier can be answered using BlockSim. Regardless of the approach used (i.e., RBD or FTA), the answers are the same.
- The reliability of the component at 1 year (8,760 hours) can be calculated using the Analytical Quick Calculation Pad (QCP) or by viewing the reliability vs. time plot, as displayed in the following figure. [math]\displaystyle{ R(t=8760)=86.4975% }[/math].
- Using the Analytical QCP, the B10 life of the component is estimated to be 7,373.94 hours.
- 3. Using the Analytical QCP, the mean life of the component is estimated to be 21,659.68 hours.
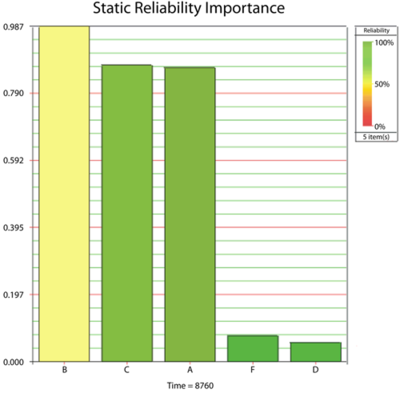
- 4. The ranking of the modes after 1 year can be shown via the Static Reliability Importance plot, as shown in the figure below.
- 5. Re-computing the results for 1, 2 and 3 assuming mode B is removed:
- a) [math]\displaystyle{ R(t=8760)=98.72%. }[/math]
- b) [math]\displaystyle{ B10 }[/math] = 16,928.38 hours.
- c) MTTF = 34,552.89 hours.
- 5. Re-computing the results for 1, 2 and 3 assuming mode B is removed:
There are multiple options for modeling systems with fault trees and RBDs in BlockSim. The first figure below shows the complete fault tree for the component without using subdiagrams (Transfer gates) while the second figure below illustrates a hybrid analysis utilizing an RBD for the component and fault trees as the subdiagrams. The results are the same regardless of the option chosen.