1-Parameter Weibull Example: Difference between revisions
No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
<noinclude>{{Banner Weibull Examples}}</noinclude> | <noinclude>{{Banner Weibull Examples}}</noinclude> | ||
'''Weibull++ Standard Folio Data 1P-Weibull''' | '''Weibull++ Standard Folio Data 1P-Weibull''' | ||
Six prototypes of a system were tested. The failure times are 16, 34, 53, 75, 93 and 120. Due to the small sample size, the 1P-Weibull distribution is chosen to model the data. According to previous similar products, the slope parameter <math>\beta </math> is 1.5. | Six prototypes of a system were tested. The failure times are 16, 34, 53, 75, 93 and 120. Due to the small sample size, the 1P-Weibull distribution is chosen to model the data. According to previous similar products, the slope parameter <math>\beta </math> is 1.5. | ||
'''Solution''' | '''Solution''' | ||
Latest revision as of 03:24, 8 August 2012
New format available! This reference is now available in a new format that offers faster page load, improved display for calculations and images and more targeted search.
As of January 2024, this Reliawiki page will not continue to be updated. Please update all links and bookmarks to the latest references at Weibull examples and Weibull reference examples.
Weibull++ Standard Folio Data 1P-Weibull
Six prototypes of a system were tested. The failure times are 16, 34, 53, 75, 93 and 120. Due to the small sample size, the 1P-Weibull distribution is chosen to model the data. According to previous similar products, the slope parameter [math]\displaystyle{ \beta }[/math] is 1.5.
Solution
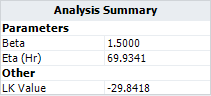
Choose the 1P-Weibull distribution in Weibull++ and calculate it, the results are given below.
- Estimated model parameters:
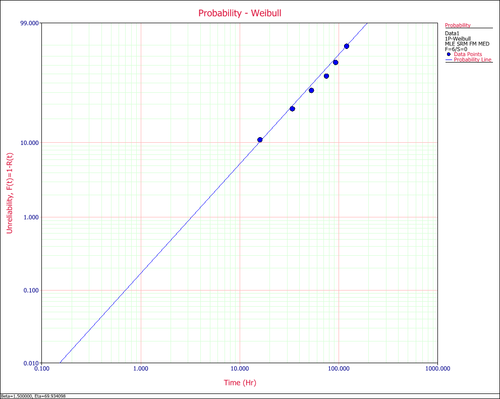
- Probability plot:
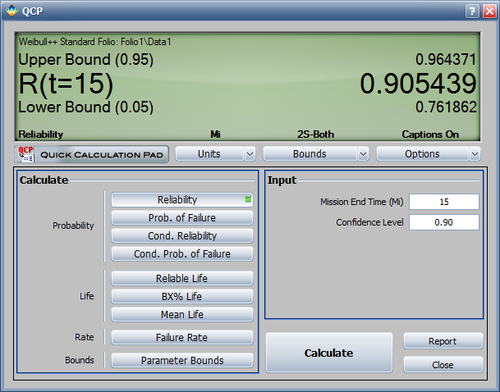
- Use the QCP to predict reliability:
The QCP shows that the reliability at 15 hours is 0.9054, and its two-sided confidence bounds at a confidence level of 90% are 0.7619 and 0.9644.