Template:Example: Median Rank Plot Example: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of ten. This will be used to illustrate two of the built-in functions in Weibull++'s '''Quick Statistical Reference'''. | In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of ten. This will be used to illustrate two of the built-in functions in Weibull++'s '''Quick Statistical Reference'''. | ||
'''Solution''' | '''Solution''' | ||
| Line 17: | Line 16: | ||
::<math>MR=\frac{1}{1+\left( \frac{10-6+1}{6} \right){{F}_{0.5;10;12}}}</math> | ::<math>MR=\frac{1}{1+\left( \frac{10-6+1}{6} \right){{F}_{0.5;10;12}}}</math> | ||
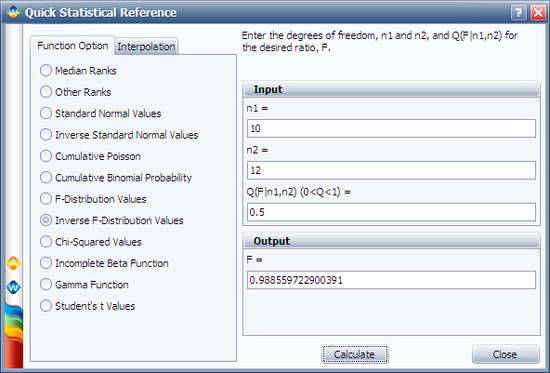
Calculate the value of F0.50:10:12 by using the Inverse F-Distribution Values option from the '''Quick Statistical Reference''', or F0.50;10;12 = 0.9886 as shown next: | Calculate the value of F0.50:10:12 by using the Inverse F-Distribution Values option from the '''Quick Statistical Reference''', or F0.50;10;12 = 0.9886 as shown next: | ||
Revision as of 05:31, 6 August 2012
Median Rank Plot Example
In this example, we will determine the median rank value used for plotting the sixth failure from a sample size of ten. This will be used to illustrate two of the built-in functions in Weibull++'s Quick Statistical Reference.
Solution
First, open the Quick Statistical Reference by clicking its icon.
or by selecting Quick Statistical Reference from the Home menu.
In this example N = 10, j = 6, m = 2(10 - 6 + 1) = 10, and n = 2 x 6 = 12.
Thus, from the F-distribution rank equation:
- [math]\displaystyle{ MR=\frac{1}{1+\left( \frac{10-6+1}{6} \right){{F}_{0.5;10;12}}} }[/math]
Calculate the value of F0.50:10:12 by using the Inverse F-Distribution Values option from the Quick Statistical Reference, or F0.50;10;12 = 0.9886 as shown next:
Consequently:
- [math]\displaystyle{ MR=\frac{1}{1+\left( \frac{5}{6} \right)\times 0.9886}=0.5483=54.83% }[/math]
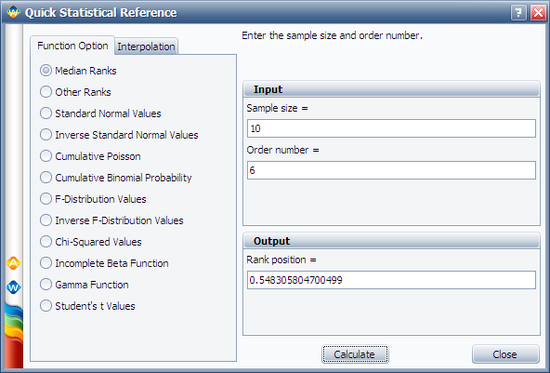
Another method is to use the Median Ranks option directly, which yields MR(%) = 54.8305%, as shown next: