Template:Probability Plotting Example (EXP1-1): Difference between revisions
Lisa Hacker (talk | contribs) |
Lisa Hacker (talk | contribs) |
||
| Line 49: | Line 49: | ||
On an exponential probability paper, plot the times on the x-axis and their corresponding | On an exponential probability paper, plot the times on the x-axis and their corresponding | ||
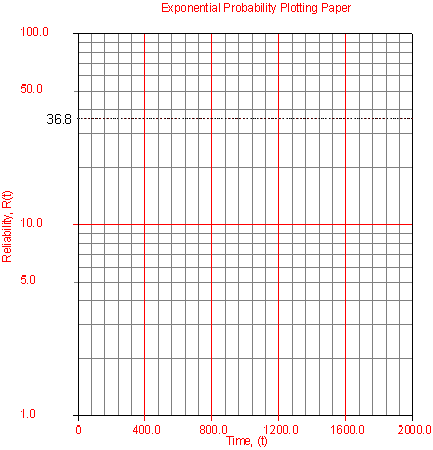
rank value on the y-axis. Fig. 4 displays an example of an exponential probability paper. The | rank value on the y-axis. Fig. 4 displays an example of an exponential probability paper. The | ||
paper is simply a log-linear paper. | paper is simply a log-linear paper. | ||
<br> | <br> | ||
| Line 56: | Line 56: | ||
<center>Fig. 4: Sample exponential probability paper.</center> | <center>Fig. 4: Sample exponential probability paper.</center> | ||
<br> | <br> | ||
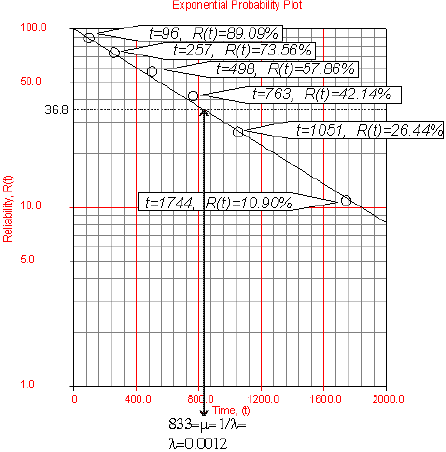
Draw the best possible straight line that goes through the <math>t=0</math> and <math> | Draw the best possible straight line that goes through the <math>t=0</math> and <math> | ||
(t)=100%</math> point and through the plotted points (as shown in Fig. 5). | (t)=100%</math> point and through the plotted points (as shown in Fig. 5). | ||
<br> | <br> | ||
At the <math>Q(t)=63.2%</math> or <math>R(t)=36.8%</math> ordinate point, draw a | At the <math>Q(t)=63.2%</math> or <math>R(t)=36.8%</math> ordinate point, draw a | ||
straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, <math>\widehat{\mu }=833</math> hr which means that <math>\lambda =\tfrac{1}{\mu }=0.0012</math> (This is always at 63.2% since <math>(T)=1-{{e}^{-\tfrac{\mu }{\mu }}}=1-{{e}^{-1}}=0.632=63.2%).</math> | straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, <math>\widehat{\mu }=833</math> hr which means that <math>\lambda =\tfrac{1}{\mu }=0.0012</math> (This is always at 63.2% since <math>(T)=1-{{e}^{-\tfrac{\mu }{\mu }}}=1-{{e}^{-1}}=0.632=63.2%).</math> | ||
Revision as of 12:35, 20 July 2012
Probability Plotting Example for the 1-parameter Exponential Distribution
Let's assume six identical units are reliability tested at the same application and operation
stress levels. All of these units fail during the test after operating for the following times (in hours), [math]\displaystyle{ {{T}_{i}} }[/math] : 96, 257, 498, 763, 1051 and 1744.
The steps for determining the parameters of the exponential [math]\displaystyle{ pdf }[/math] representing the
data, using probability plotting, are as follows:
Rank the times-to-failure in ascending order as shown next.
- [math]\displaystyle{ \begin{matrix} \text{Time-to-} & \text{Failure Order Number} \\ \text{failure, hr} & \text{out of a Sample Size of 6} \\ \text{96} & \text{1} \\ \text{257} & \text{2} \\ \text{498} & \text{3} \\ \text{763} & \text{4} \\ \text{1,051} & \text{5} \\ \text{1,744} & \text{6} \\ \end{matrix} }[/math]
Obtain their median rank plotting positions.
Median rank positions are used instead of other ranking methods because median ranks are at a specific confidence level (50%).
The times-to-failure, with their corresponding median ranks, are shown next:
- [math]\displaystyle{ \begin{matrix} \text{Time-to-} & \text{Median} \\ \text{failure, hr} & \text{Rank, }% \\ \text{96} & \text{10}\text{.91} \\ \text{257} & \text{26}\text{.44} \\ \text{498} & \text{42}\text{.14} \\ \text{763} & \text{57}\text{.86} \\ \text{1,051} & \text{73}\text{.56} \\ \text{1,744} & \text{89}\text{.10} \\ \end{matrix} }[/math]
On an exponential probability paper, plot the times on the x-axis and their corresponding rank value on the y-axis. Fig. 4 displays an example of an exponential probability paper. The paper is simply a log-linear paper.
Draw the best possible straight line that goes through the [math]\displaystyle{ t=0 }[/math] and [math]\displaystyle{ (t)=100% }[/math] point and through the plotted points (as shown in Fig. 5).
At the [math]\displaystyle{ Q(t)=63.2% }[/math] or [math]\displaystyle{ R(t)=36.8% }[/math] ordinate point, draw a
straight horizontal line until this line intersects the fitted straight line. Draw a vertical line through this intersection until it crosses the abscissa. The value at the intersection of the abscissa is the estimate of the mean. For this case, [math]\displaystyle{ \widehat{\mu }=833 }[/math] hr which means that [math]\displaystyle{ \lambda =\tfrac{1}{\mu }=0.0012 }[/math] (This is always at 63.2% since [math]\displaystyle{ (T)=1-{{e}^{-\tfrac{\mu }{\mu }}}=1-{{e}^{-1}}=0.632=63.2%). }[/math]
Now any reliability value for any mission time [math]\displaystyle{ t }[/math] can be obtained. For example, the
reliability for a mission of 15 hr, or any other time, can now be obtained either from the plot or analytically (i.e. using the equations given in Section [math]\displaystyle{ 5.1.1 }[/math] ).
To obtain the value from the plot, draw a vertical line from the abscissa, at [math]\displaystyle{ t=15 }[/math]
hr, to the fitted line. Draw a horizontal line from this intersection to the ordinate and read
[math]\displaystyle{ R(t) }[/math] . In this case, [math]\displaystyle{ R(t=15)=98.15% }[/math] . This can also be obtained
analytically, from the exponential reliability function.