Arrhenius Relationship: Difference between revisions
Chris Kahn (talk | contribs) |
Kate Racaza (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
{{template:ALTABOOK|4}} | {{template:ALTABOOK|4}} | ||
=Introduction= | |||
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. | The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887. | ||
=== | ===Formulation=== | ||
The Arrhenius reaction rate equation is given by: | |||
<br> | |||
::<math>R(T)=A{{e}^{-\tfrac{{{E}_{A}}}{K\cdot T}}}</math> | |||
<br> | |||
where: | |||
<br> | |||
• <math>R</math> is the speed of reaction. | |||
<br> | |||
• <math>A</math> is an unknown nonthermal constant. | |||
<br> | |||
• <math>{{E}_{A}}</math> is the activation energy ( <math>eV</math> ). | |||
<br> | |||
• <math>K</math> is the Boltzman's constant (<math>8.617385\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}})</math> | |||
<br> | |||
• <math>T</math> is the absolute temperature (Kelvin <math>)</math> . | |||
<br> | |||
The activation energy is the energy that a molecule must have to participate in the reaction. In other words, the activation energy is a measure of the effect that temperature has on the reaction. | |||
<br> | |||
The Arrhenius life-stress model is formulated by assuming that life is proportional to the inverse reaction rate of the process, thus the Arrhenius life-stress relationship is given by: | |||
<br> | |||
::<math>L(V)=C{{e}^{\tfrac{B}{V}}}</math> | |||
<br> | |||
where: | |||
• <math>L</math> represents a quantifiable life measure, such as mean life, characteristic life, median life, or <math>B(x)</math> life, etc. | |||
<br> | |||
• <math>V</math> represents the stress level (formulated for temperature and '''temperature values in absolute units, degrees Kelvin or degrees Rankine''' ). | |||
<br> | |||
• <math>C</math> is one of the model parameters to be determined, ( <math>C>0).</math> | |||
<br> | |||
• <math>B</math> is another model parameter to be determined. | |||
<br> | <br> | ||
<br> | |||
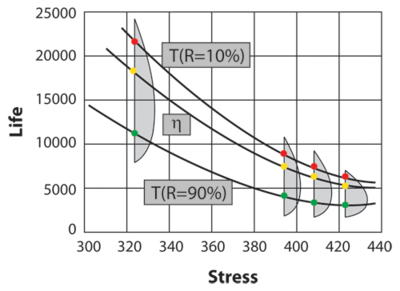
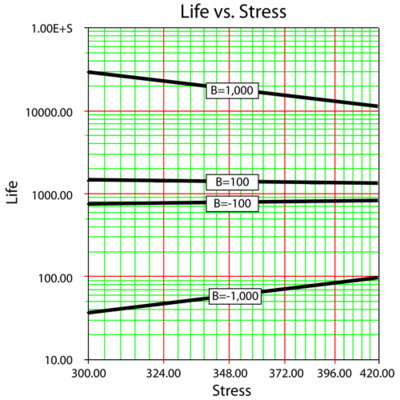
[[Image:ALTA6.1.png|center|400px|Graphical look at the Arrhenius life-stress relationship (linear scale) for a different life characteristics, assuming a Weibull distribution.]] | |||
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless. | |||
===Life Stress Plots=== | |||
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or: | The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or: | ||
<br> | <br> | ||
| Line 34: | Line 81: | ||
===Activation Energy and the Parameter ''B'' === | ===Activation Energy and the Parameter ''B'' === | ||
Depending on the application (and where the stress is exclusively thermal), the parameter <math>B</math> can be replaced by: | Depending on the application (and where the stress is exclusively thermal), the parameter <math>B</math> can be replaced by: | ||
| Line 49: | Line 95: | ||
<br> | <br> | ||
{{a-a | =Acceleration Factor= | ||
Most practitioners use the term acceleration factor to refer to the ratio of the life (or acceleration characteristic) between the use level and a higher test stress level or: | |||
<br> | |||
::<math>{{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}</math> | |||
<br> | |||
For the Arrhenius model this factor is: | |||
<br> | |||
::<math>{{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{C\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{C\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}={{e}^{\left( \tfrac{B}{{{V}_{u}}}-\tfrac{B}{{{V}_{A}}} \right)}}</math> | |||
<br> | |||
Thus, if <math>B</math> is assumed to be known a priori (using an activation energy), the assumed activation energy alone dictates this acceleration factor! | |||
<br> | |||
=Arrhenius-Exponential= | |||
The <math>pdf</math> of the 1-parameter exponential distribution is given by: | |||
<br> | |||
::<math>f(t)=\lambda {{e}^{-\lambda t}}</math> | |||
<br> | |||
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail [[Distributions used in Accelerated Testing#The Exponential Distribution|here]]) is given by: | |||
<br> | |||
::<math>\lambda =\frac{1}{m}</math> | |||
<br> | |||
thus: | |||
<br> | |||
::<math>f(t)=\frac{1}{m}{{e}^{-\tfrac{t}{m}}}</math> | |||
<br> | |||
The Arrhenius-exponential model <math>pdf</math> can then be obtained by setting <math>m=L(V)</math>: | |||
<br> | |||
Therefore: | |||
<br> | |||
::<math>m=L(V)=C{{e}^{\tfrac{B}{V}}}</math> | |||
<br> | |||
Substituting for <math>m</math> yields a <math>pdf</math> that is both a function of time and stress or: | |||
<br> | |||
::<math>f(t,V)=\frac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot {{e}^{-\tfrac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot t}}</math> | |||
<br> | |||
==Arrhenius-Exponential Statistical Properties Summary== | |||
<br> | |||
====Mean or MTTF==== | |||
The mean, <math>\overline{T},</math> or Mean Time To Failure (MTTF) of the Arrhenius-exponential is given by, | |||
<br> | |||
::<math>\begin{align} | |||
\overline{T}=\int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot \frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}}dt =\ C{{e}^{\tfrac{B}{V}}} | |||
\end{align}</math> | |||
<br> | |||
====Median==== | |||
The median, <math>\breve{T}</math> of the Arrhenius-exponential model is given by: | |||
<br> | |||
::<math>\breve{T}=0.693\cdot C{{e}^{\tfrac{B}{V}}}</math> | |||
<br> | |||
====Mode==== | |||
The mode, <math>\tilde{T},</math> | |||
of the Arrhenius-exponential model is given by: | |||
<br> | |||
::<math>\tilde{T}=0</math> | |||
<br> | |||
====Standard Deviation==== | |||
The standard deviation, <math>{{\sigma }_{T}}</math> , of the Arrhenius-exponential model is given by: | |||
<br> | |||
::<math>{{\sigma }_{T}}=C{{e}^{\tfrac{B}{V}}}</math> | |||
<br> | |||
====Arrhenius-Exponential Reliability Function==== | |||
The Arrhenius-exponential reliability function is given by: | |||
<br> | |||
::<math>R(T,V)={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}</math> | |||
<br> | |||
This function is the complement of the Arrhenius-exponential cumulative distribution function or: | |||
<br> | |||
::<math>R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT</math> | |||
<br> | |||
and: | |||
<br> | |||
::<math>R(T,V)=1-\int_{0}^{T}\frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}dT={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}</math> | |||
<br> | |||
====Conditional Reliability==== | |||
The Arrhenius-exponential conditional reliability function is given by: | |||
::<math>R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}}</math> | |||
<br> | |||
{{ | ====Reliable Life==== | ||
For the Arrhenius-exponential model, the reliable life, or the mission duration for a desired reliability goal, <math>{{t}_{R}},</math> is given by: | |||
<br> | |||
::<math>R({{t}_{R}},V)={{e}^{-\tfrac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}}}}</math> | |||
<br> | |||
::<math>\ln [R({{t}_{R}},V)]=-\frac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}}</math> | |||
<br> | |||
or: | |||
<br> | |||
::<math>{{t}_{R}}=-C{{e}^{\tfrac{B}{V}}}\ln [R({{t}_{R}},V)]</math> | |||
<br> | |||
==Parameter Estimation== | |||
====Maximum Likelihood Estimation Method==== | |||
The log-likelihood function for the exponential distribution is as shown next: | |||
<br> | |||
::<math>\begin{align} | |||
& \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime } \ | |||
& \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] | |||
\end{align}</math> | |||
<br> | |||
where: | |||
<br> | |||
::<math>R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}}</math> | |||
<br> | |||
::<math>R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}}</math> | |||
<br> | |||
and: | |||
<br> | |||
• <math>{{F}_{e}}</math> is the number of groups of exact times-to-failure data points. | |||
• <math>{{N}_{i}}</math> is the number of times-to-failure in the <math>{{i}^{th}}</math> time-to-failure data group. | |||
• <math>\lambda </math> is the failure rate parameter (unknown). | |||
• <math>{{T}_{i}}</math> is the exact failure time of the <math>{{i}^{th}}</math> group. | |||
• <math>S</math> is the number of groups of suspension data points. | |||
• <math>N_{i}^{\prime }</math> is the number of suspensions in the <math>{{i}^{th}}</math> group of suspension data points. | |||
• <math>T_{i}^{\prime }</math> is the time of the <math>{{i}^{th}}</math> suspension data group. | |||
• <math>FI</math> is the number of interval data groups. | |||
• <math>N_{i}^{\prime \prime }</math> is the number of intervals in the <math>{{i}^{th}}</math> group of data intervals. | |||
• <math>T_{Li}^{\prime \prime }</math> is the beginning of the <math>{{i}^{th}}</math> interval. | |||
• <math>T_{Ri}^{\prime \prime }</math> is the ending of the <math>{{i}^{th}}</math> interval. | |||
<br> | |||
Substituting the Arrhenius-exponential model into the log-likelihood function yields: | |||
<br> | |||
::<math>\begin{align} | |||
\Lambda = \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{e}^{-\tfrac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] | |||
\end{align}</math> | |||
<br> | |||
where: | |||
<br> | |||
::<math>R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}}</math> | |||
<br> | |||
::<math>R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}}</math> | |||
<br> | |||
The solution (parameter estimates) will be found by solving for the parameters <math>\widehat{B},</math> <math>\widehat{C}</math> so that <math>\tfrac{\partial \Lambda }{\partial B}=0</math> and <math>\tfrac{\partial \Lambda }{\partial C}=0</math> , where: | |||
<br> | |||
::<math>\begin{align} | |||
& \frac{\partial \Lambda }{\partial B}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}}-\frac{C}{{{V}_{i}}} \right)+\frac{1}{C}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime })C{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} | |||
\end{align}</math> | |||
<br> | |||
::<math>\begin{align} | |||
& \frac{\partial \Lambda }{\partial C}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}-1 \right)+\frac{1}{{{C}^{2}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }){{C}^{2}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} | |||
\end{align}</math> | |||
<br> | |||
=Arrhenius-Weibull= | |||
<br> | <br> | ||
The <math>pdf</math> for the 2-parameter Weibull distribution is given by: | The <math>pdf</math> for the 2-parameter Weibull distribution is given by: | ||
<br> | <br> | ||
{{weibull2pdf}} | |||
<br> | <br> | ||
| Line 87: | Line 354: | ||
{{aaw stat prob sum}} | {{aaw stat prob sum}} | ||
==Parameter Estimation== | |||
<br> | <br> | ||
{{aaw mle}} | {{aaw mle}} | ||
Revision as of 10:19, 3 July 2012
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887.
Formulation
The Arrhenius reaction rate equation is given by:
- [math]\displaystyle{ R(T)=A{{e}^{-\tfrac{{{E}_{A}}}{K\cdot T}}} }[/math]
where:
• [math]\displaystyle{ R }[/math] is the speed of reaction.
• [math]\displaystyle{ A }[/math] is an unknown nonthermal constant.
• [math]\displaystyle{ {{E}_{A}} }[/math] is the activation energy ( [math]\displaystyle{ eV }[/math] ).
• [math]\displaystyle{ K }[/math] is the Boltzman's constant ([math]\displaystyle{ 8.617385\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}) }[/math]
• [math]\displaystyle{ T }[/math] is the absolute temperature (Kelvin [math]\displaystyle{ ) }[/math] .
The activation energy is the energy that a molecule must have to participate in the reaction. In other words, the activation energy is a measure of the effect that temperature has on the reaction.
The Arrhenius life-stress model is formulated by assuming that life is proportional to the inverse reaction rate of the process, thus the Arrhenius life-stress relationship is given by:
- [math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, or [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (formulated for temperature and temperature values in absolute units, degrees Kelvin or degrees Rankine ).
• [math]\displaystyle{ C }[/math] is one of the model parameters to be determined, ( [math]\displaystyle{ C\gt 0). }[/math]
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless.
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
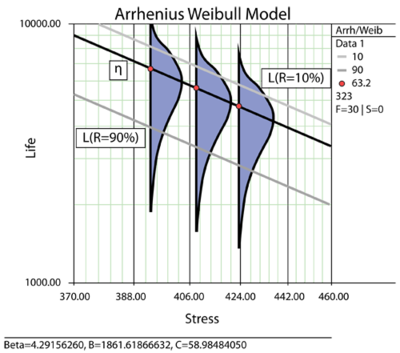
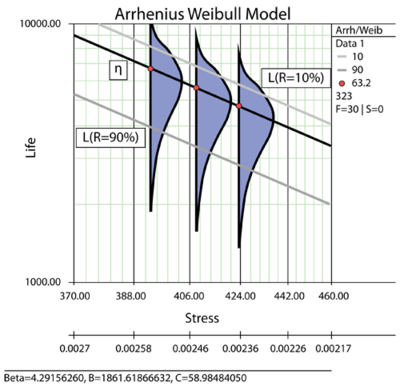
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
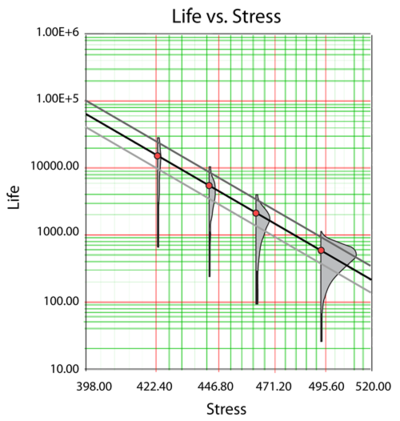
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Acceleration Factor
Most practitioners use the term acceleration factor to refer to the ratio of the life (or acceleration characteristic) between the use level and a higher test stress level or:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}} }[/math]
For the Arrhenius model this factor is:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{C\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{C\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}={{e}^{\left( \tfrac{B}{{{V}_{u}}}-\tfrac{B}{{{V}_{A}}} \right)}} }[/math]
Thus, if [math]\displaystyle{ B }[/math] is assumed to be known a priori (using an activation energy), the assumed activation energy alone dictates this acceleration factor!
Arrhenius-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda {{e}^{-\lambda t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}{{e}^{-\tfrac{t}{m}}} }[/math]
The Arrhenius-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
Therefore:
- [math]\displaystyle{ m=L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
Substituting for [math]\displaystyle{ m }[/math] yields a [math]\displaystyle{ pdf }[/math] that is both a function of time and stress or:
- [math]\displaystyle{ f(t,V)=\frac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot {{e}^{-\tfrac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot t}} }[/math]
Arrhenius-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) of the Arrhenius-exponential is given by,
- [math]\displaystyle{ \begin{align} \overline{T}=\int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot \frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}}dt =\ C{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T} }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\cdot C{{e}^{\tfrac{B}{V}}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \tilde{T}=0 }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=C{{e}^{\tfrac{B}{V}}} }[/math]
Arrhenius-Exponential Reliability Function
The Arrhenius-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
This function is the complement of the Arrhenius-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}\frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}dT={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Conditional Reliability
The Arrhenius-exponential conditional reliability function is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Reliable Life
For the Arrhenius-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-\tfrac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-\frac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-C{{e}^{\tfrac{B}{V}}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The log-likelihood function for the exponential distribution is as shown next:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime } \ & \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \lambda }[/math] is the failure rate parameter (unknown).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
Substituting the Arrhenius-exponential model into the log-likelihood function yields:
- [math]\displaystyle{ \begin{align} \Lambda = \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{e}^{-\tfrac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0 }[/math] , where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}}-\frac{C}{{{V}_{i}}} \right)+\frac{1}{C}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime })C{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial C}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}-1 \right)+\frac{1}{{{C}^{2}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }){{C}^{2}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887.
Formulation
The Arrhenius reaction rate equation is given by:
- [math]\displaystyle{ R(T)=A{{e}^{-\tfrac{{{E}_{A}}}{K\cdot T}}} }[/math]
where:
• [math]\displaystyle{ R }[/math] is the speed of reaction.
• [math]\displaystyle{ A }[/math] is an unknown nonthermal constant.
• [math]\displaystyle{ {{E}_{A}} }[/math] is the activation energy ( [math]\displaystyle{ eV }[/math] ).
• [math]\displaystyle{ K }[/math] is the Boltzman's constant ([math]\displaystyle{ 8.617385\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}) }[/math]
• [math]\displaystyle{ T }[/math] is the absolute temperature (Kelvin [math]\displaystyle{ ) }[/math] .
The activation energy is the energy that a molecule must have to participate in the reaction. In other words, the activation energy is a measure of the effect that temperature has on the reaction.
The Arrhenius life-stress model is formulated by assuming that life is proportional to the inverse reaction rate of the process, thus the Arrhenius life-stress relationship is given by:
- [math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, or [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (formulated for temperature and temperature values in absolute units, degrees Kelvin or degrees Rankine ).
• [math]\displaystyle{ C }[/math] is one of the model parameters to be determined, ( [math]\displaystyle{ C\gt 0). }[/math]
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless.
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Acceleration Factor
Most practitioners use the term acceleration factor to refer to the ratio of the life (or acceleration characteristic) between the use level and a higher test stress level or:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}} }[/math]
For the Arrhenius model this factor is:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{C\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{C\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}={{e}^{\left( \tfrac{B}{{{V}_{u}}}-\tfrac{B}{{{V}_{A}}} \right)}} }[/math]
Thus, if [math]\displaystyle{ B }[/math] is assumed to be known a priori (using an activation energy), the assumed activation energy alone dictates this acceleration factor!
Arrhenius-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda {{e}^{-\lambda t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}{{e}^{-\tfrac{t}{m}}} }[/math]
The Arrhenius-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
Therefore:
- [math]\displaystyle{ m=L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
Substituting for [math]\displaystyle{ m }[/math] yields a [math]\displaystyle{ pdf }[/math] that is both a function of time and stress or:
- [math]\displaystyle{ f(t,V)=\frac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot {{e}^{-\tfrac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot t}} }[/math]
Arrhenius-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) of the Arrhenius-exponential is given by,
- [math]\displaystyle{ \begin{align} \overline{T}=\int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot \frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}}dt =\ C{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T} }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\cdot C{{e}^{\tfrac{B}{V}}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \tilde{T}=0 }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=C{{e}^{\tfrac{B}{V}}} }[/math]
Arrhenius-Exponential Reliability Function
The Arrhenius-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
This function is the complement of the Arrhenius-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}\frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}dT={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Conditional Reliability
The Arrhenius-exponential conditional reliability function is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Reliable Life
For the Arrhenius-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-\tfrac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-\frac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-C{{e}^{\tfrac{B}{V}}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The log-likelihood function for the exponential distribution is as shown next:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime } \ & \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \lambda }[/math] is the failure rate parameter (unknown).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
Substituting the Arrhenius-exponential model into the log-likelihood function yields:
- [math]\displaystyle{ \begin{align} \Lambda = \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{e}^{-\tfrac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0 }[/math] , where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}}-\frac{C}{{{V}_{i}}} \right)+\frac{1}{C}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime })C{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial C}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}-1 \right)+\frac{1}{{{C}^{2}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }){{C}^{2}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
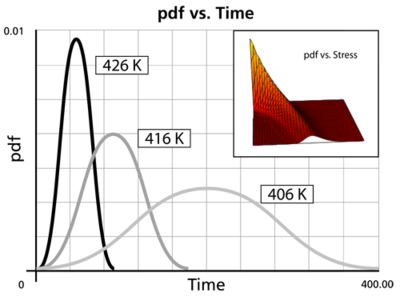
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
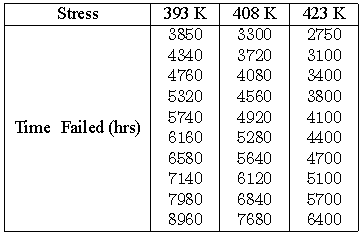
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
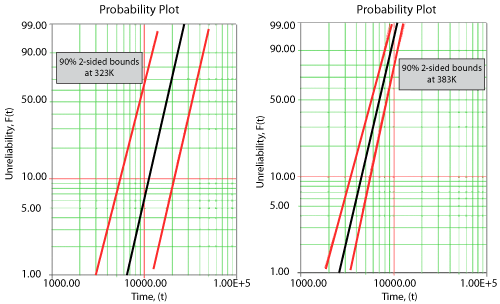
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887.
Formulation
The Arrhenius reaction rate equation is given by:
- [math]\displaystyle{ R(T)=A{{e}^{-\tfrac{{{E}_{A}}}{K\cdot T}}} }[/math]
where:
• [math]\displaystyle{ R }[/math] is the speed of reaction.
• [math]\displaystyle{ A }[/math] is an unknown nonthermal constant.
• [math]\displaystyle{ {{E}_{A}} }[/math] is the activation energy ( [math]\displaystyle{ eV }[/math] ).
• [math]\displaystyle{ K }[/math] is the Boltzman's constant ([math]\displaystyle{ 8.617385\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}) }[/math]
• [math]\displaystyle{ T }[/math] is the absolute temperature (Kelvin [math]\displaystyle{ ) }[/math] .
The activation energy is the energy that a molecule must have to participate in the reaction. In other words, the activation energy is a measure of the effect that temperature has on the reaction.
The Arrhenius life-stress model is formulated by assuming that life is proportional to the inverse reaction rate of the process, thus the Arrhenius life-stress relationship is given by:
- [math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, or [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (formulated for temperature and temperature values in absolute units, degrees Kelvin or degrees Rankine ).
• [math]\displaystyle{ C }[/math] is one of the model parameters to be determined, ( [math]\displaystyle{ C\gt 0). }[/math]
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless.
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Acceleration Factor
Most practitioners use the term acceleration factor to refer to the ratio of the life (or acceleration characteristic) between the use level and a higher test stress level or:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}} }[/math]
For the Arrhenius model this factor is:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{C\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{C\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}={{e}^{\left( \tfrac{B}{{{V}_{u}}}-\tfrac{B}{{{V}_{A}}} \right)}} }[/math]
Thus, if [math]\displaystyle{ B }[/math] is assumed to be known a priori (using an activation energy), the assumed activation energy alone dictates this acceleration factor!
Arrhenius-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda {{e}^{-\lambda t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}{{e}^{-\tfrac{t}{m}}} }[/math]
The Arrhenius-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
Therefore:
- [math]\displaystyle{ m=L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
Substituting for [math]\displaystyle{ m }[/math] yields a [math]\displaystyle{ pdf }[/math] that is both a function of time and stress or:
- [math]\displaystyle{ f(t,V)=\frac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot {{e}^{-\tfrac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot t}} }[/math]
Arrhenius-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) of the Arrhenius-exponential is given by,
- [math]\displaystyle{ \begin{align} \overline{T}=\int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot \frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}}dt =\ C{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T} }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\cdot C{{e}^{\tfrac{B}{V}}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \tilde{T}=0 }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=C{{e}^{\tfrac{B}{V}}} }[/math]
Arrhenius-Exponential Reliability Function
The Arrhenius-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
This function is the complement of the Arrhenius-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}\frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}dT={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Conditional Reliability
The Arrhenius-exponential conditional reliability function is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Reliable Life
For the Arrhenius-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-\tfrac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-\frac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-C{{e}^{\tfrac{B}{V}}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The log-likelihood function for the exponential distribution is as shown next:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime } \ & \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \lambda }[/math] is the failure rate parameter (unknown).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
Substituting the Arrhenius-exponential model into the log-likelihood function yields:
- [math]\displaystyle{ \begin{align} \Lambda = \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{e}^{-\tfrac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0 }[/math] , where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}}-\frac{C}{{{V}_{i}}} \right)+\frac{1}{C}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime })C{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial C}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}-1 \right)+\frac{1}{{{C}^{2}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }){{C}^{2}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Parameter Estimation
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887.
Formulation
The Arrhenius reaction rate equation is given by:
- [math]\displaystyle{ R(T)=A{{e}^{-\tfrac{{{E}_{A}}}{K\cdot T}}} }[/math]
where:
• [math]\displaystyle{ R }[/math] is the speed of reaction.
• [math]\displaystyle{ A }[/math] is an unknown nonthermal constant.
• [math]\displaystyle{ {{E}_{A}} }[/math] is the activation energy ( [math]\displaystyle{ eV }[/math] ).
• [math]\displaystyle{ K }[/math] is the Boltzman's constant ([math]\displaystyle{ 8.617385\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}) }[/math]
• [math]\displaystyle{ T }[/math] is the absolute temperature (Kelvin [math]\displaystyle{ ) }[/math] .
The activation energy is the energy that a molecule must have to participate in the reaction. In other words, the activation energy is a measure of the effect that temperature has on the reaction.
The Arrhenius life-stress model is formulated by assuming that life is proportional to the inverse reaction rate of the process, thus the Arrhenius life-stress relationship is given by:
- [math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, or [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (formulated for temperature and temperature values in absolute units, degrees Kelvin or degrees Rankine ).
• [math]\displaystyle{ C }[/math] is one of the model parameters to be determined, ( [math]\displaystyle{ C\gt 0). }[/math]
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless.
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Acceleration Factor
Most practitioners use the term acceleration factor to refer to the ratio of the life (or acceleration characteristic) between the use level and a higher test stress level or:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}} }[/math]
For the Arrhenius model this factor is:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{C\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{C\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}={{e}^{\left( \tfrac{B}{{{V}_{u}}}-\tfrac{B}{{{V}_{A}}} \right)}} }[/math]
Thus, if [math]\displaystyle{ B }[/math] is assumed to be known a priori (using an activation energy), the assumed activation energy alone dictates this acceleration factor!
Arrhenius-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda {{e}^{-\lambda t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}{{e}^{-\tfrac{t}{m}}} }[/math]
The Arrhenius-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
Therefore:
- [math]\displaystyle{ m=L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
Substituting for [math]\displaystyle{ m }[/math] yields a [math]\displaystyle{ pdf }[/math] that is both a function of time and stress or:
- [math]\displaystyle{ f(t,V)=\frac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot {{e}^{-\tfrac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot t}} }[/math]
Arrhenius-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) of the Arrhenius-exponential is given by,
- [math]\displaystyle{ \begin{align} \overline{T}=\int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot \frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}}dt =\ C{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T} }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\cdot C{{e}^{\tfrac{B}{V}}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \tilde{T}=0 }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=C{{e}^{\tfrac{B}{V}}} }[/math]
Arrhenius-Exponential Reliability Function
The Arrhenius-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
This function is the complement of the Arrhenius-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}\frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}dT={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Conditional Reliability
The Arrhenius-exponential conditional reliability function is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Reliable Life
For the Arrhenius-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-\tfrac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-\frac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-C{{e}^{\tfrac{B}{V}}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The log-likelihood function for the exponential distribution is as shown next:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime } \ & \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \lambda }[/math] is the failure rate parameter (unknown).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
Substituting the Arrhenius-exponential model into the log-likelihood function yields:
- [math]\displaystyle{ \begin{align} \Lambda = \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{e}^{-\tfrac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0 }[/math] , where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}}-\frac{C}{{{V}_{i}}} \right)+\frac{1}{C}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime })C{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial C}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}-1 \right)+\frac{1}{{{C}^{2}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }){{C}^{2}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887.
Formulation
The Arrhenius reaction rate equation is given by:
- [math]\displaystyle{ R(T)=A{{e}^{-\tfrac{{{E}_{A}}}{K\cdot T}}} }[/math]
where:
• [math]\displaystyle{ R }[/math] is the speed of reaction.
• [math]\displaystyle{ A }[/math] is an unknown nonthermal constant.
• [math]\displaystyle{ {{E}_{A}} }[/math] is the activation energy ( [math]\displaystyle{ eV }[/math] ).
• [math]\displaystyle{ K }[/math] is the Boltzman's constant ([math]\displaystyle{ 8.617385\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}) }[/math]
• [math]\displaystyle{ T }[/math] is the absolute temperature (Kelvin [math]\displaystyle{ ) }[/math] .
The activation energy is the energy that a molecule must have to participate in the reaction. In other words, the activation energy is a measure of the effect that temperature has on the reaction.
The Arrhenius life-stress model is formulated by assuming that life is proportional to the inverse reaction rate of the process, thus the Arrhenius life-stress relationship is given by:
- [math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, or [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (formulated for temperature and temperature values in absolute units, degrees Kelvin or degrees Rankine ).
• [math]\displaystyle{ C }[/math] is one of the model parameters to be determined, ( [math]\displaystyle{ C\gt 0). }[/math]
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless.
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Acceleration Factor
Most practitioners use the term acceleration factor to refer to the ratio of the life (or acceleration characteristic) between the use level and a higher test stress level or:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}} }[/math]
For the Arrhenius model this factor is:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{C\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{C\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}={{e}^{\left( \tfrac{B}{{{V}_{u}}}-\tfrac{B}{{{V}_{A}}} \right)}} }[/math]
Thus, if [math]\displaystyle{ B }[/math] is assumed to be known a priori (using an activation energy), the assumed activation energy alone dictates this acceleration factor!
Arrhenius-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda {{e}^{-\lambda t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}{{e}^{-\tfrac{t}{m}}} }[/math]
The Arrhenius-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
Therefore:
- [math]\displaystyle{ m=L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
Substituting for [math]\displaystyle{ m }[/math] yields a [math]\displaystyle{ pdf }[/math] that is both a function of time and stress or:
- [math]\displaystyle{ f(t,V)=\frac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot {{e}^{-\tfrac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot t}} }[/math]
Arrhenius-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) of the Arrhenius-exponential is given by,
- [math]\displaystyle{ \begin{align} \overline{T}=\int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot \frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}}dt =\ C{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T} }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\cdot C{{e}^{\tfrac{B}{V}}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \tilde{T}=0 }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=C{{e}^{\tfrac{B}{V}}} }[/math]
Arrhenius-Exponential Reliability Function
The Arrhenius-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
This function is the complement of the Arrhenius-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}\frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}dT={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Conditional Reliability
The Arrhenius-exponential conditional reliability function is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Reliable Life
For the Arrhenius-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-\tfrac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-\frac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-C{{e}^{\tfrac{B}{V}}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The log-likelihood function for the exponential distribution is as shown next:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime } \ & \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \lambda }[/math] is the failure rate parameter (unknown).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
Substituting the Arrhenius-exponential model into the log-likelihood function yields:
- [math]\displaystyle{ \begin{align} \Lambda = \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{e}^{-\tfrac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0 }[/math] , where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}}-\frac{C}{{{V}_{i}}} \right)+\frac{1}{C}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime })C{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial C}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}-1 \right)+\frac{1}{{{C}^{2}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }){{C}^{2}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds
Introduction
The Arrhenius life-stress model (or relationship) is probably the most common life-stress relationship utilized in accelerated life testing. It has been widely used when the stimulus or acceleration variable (or stress) is thermal (i.e., temperature). It is derived from the Arrhenius reaction rate equation proposed by the Swedish physical chemist Svandte Arrhenius in 1887.
Formulation
The Arrhenius reaction rate equation is given by:
- [math]\displaystyle{ R(T)=A{{e}^{-\tfrac{{{E}_{A}}}{K\cdot T}}} }[/math]
where:
• [math]\displaystyle{ R }[/math] is the speed of reaction.
• [math]\displaystyle{ A }[/math] is an unknown nonthermal constant.
• [math]\displaystyle{ {{E}_{A}} }[/math] is the activation energy ( [math]\displaystyle{ eV }[/math] ).
• [math]\displaystyle{ K }[/math] is the Boltzman's constant ([math]\displaystyle{ 8.617385\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}) }[/math]
• [math]\displaystyle{ T }[/math] is the absolute temperature (Kelvin [math]\displaystyle{ ) }[/math] .
The activation energy is the energy that a molecule must have to participate in the reaction. In other words, the activation energy is a measure of the effect that temperature has on the reaction.
The Arrhenius life-stress model is formulated by assuming that life is proportional to the inverse reaction rate of the process, thus the Arrhenius life-stress relationship is given by:
- [math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, or [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (formulated for temperature and temperature values in absolute units, degrees Kelvin or degrees Rankine ).
• [math]\displaystyle{ C }[/math] is one of the model parameters to be determined, ( [math]\displaystyle{ C\gt 0). }[/math]
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless.
Life Stress Plots
The Arrhenius relationship can be linearized and plotted on a Life vs. Stress plot, also called the Arrhenius plot. The relationship is linearized by taking the natural logarithm of both sides in the Arrhenius equation or:
- [math]\displaystyle{ ln(L(V))=ln(C)+\frac{B}{V} }[/math]
- [math]\displaystyle{ }[/math]
In the linearized Arrhenius equation, [math]\displaystyle{ \ln (C) }[/math] is the intercept of the line and [math]\displaystyle{ B }[/math] is the slope of the line. Note that the inverse of the stress, and not the stress, is the variable. In the above figure, life is plotted versus stress and not versus the inverse stress. This is because the linearized Arrhenius equation was plotted on a reciprocal scale. On such a scale, the slope [math]\displaystyle{ B }[/math] appears to be negative even though it has a positive value. This is because [math]\displaystyle{ B }[/math] is actually the slope of the reciprocal of the stress and not the slope of the stress. The reciprocal of the stress is decreasing as stress is increasing ( [math]\displaystyle{ \tfrac{1}{V} }[/math] is decreasing as [math]\displaystyle{ V }[/math] is increasing). The two different axes are shown in the next figure.
- [math]\displaystyle{ }[/math]
The Arrhenius relationship is plotted on a reciprocal scale for practical reasons. For example, in the above figure it is more convenient to locate the life corresponding to a stress level of 370K than to take the reciprocal of 370K (0.0027) first, and then locate the corresponding life.
The shaded areas shown in the above figure are the imposed at each test stress level. From such imposed [math]\displaystyle{ pdfs }[/math] one can see the range of the life at each test stress level, as well as the scatter in life. The next figure illustrates a case in which there is a significant scatter in life at each of the test stress levels.
- [math]\displaystyle{ }[/math]
Activation Energy and the Parameter B
Depending on the application (and where the stress is exclusively thermal), the parameter [math]\displaystyle{ B }[/math] can be replaced by:
- [math]\displaystyle{ B=-\frac{{{E}_{A}}}{K}=-\frac{\text{activation energy}}{\text{Boltzma}{{\text{n}}^{\prime }}\text{s constant}}=-\frac{\text{activation energy}}{8.623\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}} }[/math]
Note that in this formulation, the activation energy [math]\displaystyle{ {{E}_{A}} }[/math] must be known a priori. If the activation energy is known then there is only one model parameter remaining, [math]\displaystyle{ C. }[/math] Because in most real life situations this is rarely the case, all subsequent formulations will assume that this activation energy is unknown and treat [math]\displaystyle{ B }[/math] as one of the model parameters. [math]\displaystyle{ B }[/math] has the same properties as the activation energy. In other words, [math]\displaystyle{ B }[/math] is a measure of the effect that the stress (i.e. temperature) has on the life. The larger the value of [math]\displaystyle{ B, }[/math] the higher the dependency of the life on the specific stress. Parameter [math]\displaystyle{ B }[/math] may also take negative values. In that case, life is increasing with increasing stress. An example of this would be plasma filled bulbs, where low temperature is a higher stress on the bulbs than high temperature.
- [math]\displaystyle{ }[/math]
Acceleration Factor
Most practitioners use the term acceleration factor to refer to the ratio of the life (or acceleration characteristic) between the use level and a higher test stress level or:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}} }[/math]
For the Arrhenius model this factor is:
- [math]\displaystyle{ {{A}_{F}}=\frac{{{L}_{USE}}}{{{L}_{Accelerated}}}=\frac{C\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{C\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}=\frac{\text{ }{{e}^{\tfrac{B}{{{V}_{u}}}}}}{\text{ }{{e}^{\tfrac{B}{{{V}_{A}}}}}}={{e}^{\left( \tfrac{B}{{{V}_{u}}}-\tfrac{B}{{{V}_{A}}} \right)}} }[/math]
Thus, if [math]\displaystyle{ B }[/math] is assumed to be known a priori (using an activation energy), the assumed activation energy alone dictates this acceleration factor!
Arrhenius-Exponential
The [math]\displaystyle{ pdf }[/math] of the 1-parameter exponential distribution is given by:
- [math]\displaystyle{ f(t)=\lambda {{e}^{-\lambda t}} }[/math]
It can be easily shown that the mean life for the 1-parameter exponential distribution (presented in detail here) is given by:
- [math]\displaystyle{ \lambda =\frac{1}{m} }[/math]
thus:
- [math]\displaystyle{ f(t)=\frac{1}{m}{{e}^{-\tfrac{t}{m}}} }[/math]
The Arrhenius-exponential model [math]\displaystyle{ pdf }[/math] can then be obtained by setting [math]\displaystyle{ m=L(V) }[/math]:
Therefore:
- [math]\displaystyle{ m=L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
Substituting for [math]\displaystyle{ m }[/math] yields a [math]\displaystyle{ pdf }[/math] that is both a function of time and stress or:
- [math]\displaystyle{ f(t,V)=\frac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot {{e}^{-\tfrac{1}{C{{e}^{\tfrac{B}{V}}}}\cdot t}} }[/math]
Arrhenius-Exponential Statistical Properties Summary
Mean or MTTF
The mean, [math]\displaystyle{ \overline{T}, }[/math] or Mean Time To Failure (MTTF) of the Arrhenius-exponential is given by,
- [math]\displaystyle{ \begin{align} \overline{T}=\int_{0}^{\infty }t\cdot f(t,V)dt=\int_{0}^{\infty }t\cdot \frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}}dt =\ C{{e}^{\tfrac{B}{V}}} \end{align} }[/math]
Median
The median, [math]\displaystyle{ \breve{T} }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \breve{T}=0.693\cdot C{{e}^{\tfrac{B}{V}}} }[/math]
Mode
The mode, [math]\displaystyle{ \tilde{T}, }[/math] of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ \tilde{T}=0 }[/math]
Standard Deviation
The standard deviation, [math]\displaystyle{ {{\sigma }_{T}} }[/math] , of the Arrhenius-exponential model is given by:
- [math]\displaystyle{ {{\sigma }_{T}}=C{{e}^{\tfrac{B}{V}}} }[/math]
Arrhenius-Exponential Reliability Function
The Arrhenius-exponential reliability function is given by:
- [math]\displaystyle{ R(T,V)={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
This function is the complement of the Arrhenius-exponential cumulative distribution function or:
- [math]\displaystyle{ R(T,V)=1-Q(T,V)=1-\int_{0}^{T}f(T,V)dT }[/math]
and:
- [math]\displaystyle{ R(T,V)=1-\int_{0}^{T}\frac{1}{C{{e}^{\tfrac{B}{V}}}}{{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}}dT={{e}^{-\tfrac{T}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Conditional Reliability
The Arrhenius-exponential conditional reliability function is given by:
- [math]\displaystyle{ R(T,t,V)=\frac{R(T+t,V)}{R(T,V)}=\frac{{{e}^{-\lambda (T+t)}}}{{{e}^{-\lambda T}}}={{e}^{-\tfrac{t}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
Reliable Life
For the Arrhenius-exponential model, the reliable life, or the mission duration for a desired reliability goal, [math]\displaystyle{ {{t}_{R}}, }[/math] is given by:
- [math]\displaystyle{ R({{t}_{R}},V)={{e}^{-\tfrac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}}}} }[/math]
- [math]\displaystyle{ \ln [R({{t}_{R}},V)]=-\frac{{{t}_{R}}}{C{{e}^{\tfrac{B}{V}}}} }[/math]
or:
- [math]\displaystyle{ {{t}_{R}}=-C{{e}^{\tfrac{B}{V}}}\ln [R({{t}_{R}},V)] }[/math]
Parameter Estimation
Maximum Likelihood Estimation Method
The log-likelihood function for the exponential distribution is as shown next:
- [math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \lambda {{e}^{-\lambda {{T}_{i}}}} \right]-\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\lambda T_{i}^{\prime } \ & \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\lambda T_{Li}^{\prime \prime }}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\lambda T_{Ri}^{\prime \prime }}} }[/math]
and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ \lambda }[/math] is the failure rate parameter (unknown).
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
Substituting the Arrhenius-exponential model into the log-likelihood function yields:
- [math]\displaystyle{ \begin{align} \Lambda = \underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\ln \left[ \frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{e}^{-\tfrac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}{{T}_{i}}}} \right] -\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{1}{C\cdot {{e}^{\tfrac{B}{{{V}_{i}}}}}}T_{i}^{\prime }+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]
where:
- [math]\displaystyle{ R_{Li}^{\prime \prime }={{e}^{-\tfrac{T_{Li}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
- [math]\displaystyle{ R_{Ri}^{\prime \prime }={{e}^{-\tfrac{T_{Ri}^{\prime \prime }}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}}} }[/math]
The solution (parameter estimates) will be found by solving for the parameters [math]\displaystyle{ \widehat{B}, }[/math] [math]\displaystyle{ \widehat{C} }[/math] so that [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial B}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial C}=0 }[/math] , where:
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial B}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}}-\frac{C}{{{V}_{i}}} \right)+\frac{1}{C}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime })C{{V}_{i}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
- [math]\displaystyle{ \begin{align} & \frac{\partial \Lambda }{\partial C}= & \frac{1}{C}\underset{i=1}{\overset{{{F}_{e}}}{\mathop \sum }}\,{{N}_{i}}\left( \frac{{{T}_{i}}}{C{{e}^{\tfrac{B}{{{V}_{i}}}}}}-1 \right)+\frac{1}{{{C}^{2}}}\underset{i=1}{\overset{S}{\mathop \sum }}\,N_{i}^{\prime }\frac{T_{i}^{\prime }}{{{e}^{\tfrac{B}{{{V}_{i}}}}}} \overset{FI}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\frac{T_{Li}^{\prime \prime }R_{Li}^{\prime \prime }-T_{Ri}^{\prime \prime }R_{Ri}^{\prime \prime }}{(R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }){{C}^{2}}{{e}^{\tfrac{B}{{{V}_{i}}}}}} \end{align} }[/math]
Arrhenius-Weibull
The [math]\displaystyle{ pdf }[/math] for the 2-parameter Weibull distribution is given by:
Template loop detected: Template:Weibull2pdf
The scale parameter (or characteristic life) of the Weibull distribution is [math]\displaystyle{ \eta }[/math] .
The Arrhenius-Weibull model pdf can then be obtained by setting [math]\displaystyle{ \eta =L(V) }[/math]:
- [math]\displaystyle{ \eta =L(V)=C\cdot {{e}^{\tfrac{B}{V}}} }[/math]
and substituting for [math]\displaystyle{ \eta }[/math] in the 2-parameter Weibull distribution equation:
- [math]\displaystyle{ f(t,V)=\frac{\beta }{C\cdot {{e}^{\tfrac{B}{V}}}}{{\left( \frac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta -1}}{{e}^{-{{\left( \tfrac{t}{C\cdot {{e}^{\tfrac{B}{V}}}} \right)}^{\beta }}}} }[/math]
An illustration of the [math]\displaystyle{ pdf }[/math] for different stresses is shown in the next figure. As expected, the [math]\displaystyle{ pdf }[/math] at lower stress levels is more stretched to the right, with a higher scale parameter, while its shape remains the same (the shape parameter is approximately 3). This behavior is observed when the parameter [math]\displaystyle{ B }[/math] of the Arrhenius model is positive.
The advantage of using the Weibull distribution as the life distribution lies in its flexibility to assume different shapes. The Weibull distribution is presented in greater detail here.
Template loop detected: Template:Aaw stat prob sum
Parameter Estimation
Template loop detected: Template:Aaw mle
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822\,\! }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657\,\! }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692\,\! }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure, the more distant the accelerated stress is from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in the Arrhenius Relationship chapter).
Template loop detected: Template:Alta al
Template loop detected: Template:Arrhenius confidence bounds