Template:Arrhenius-weibull example: Difference between revisions
Chris Kahn (talk | contribs) |
Chris Kahn (talk | contribs) |
||
| Line 27: | Line 27: | ||
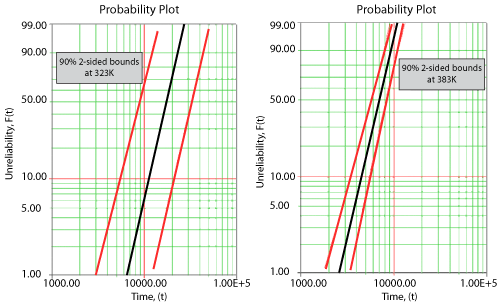
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure the more distant the accelerated stress from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in [[Appendix A: Brief Statistical Background|Appendix A]]. Specific calculations for confidence bounds on the Arrhenius model are presented in [[Arrhenius Relationship#Appendix 6.A: Arrhenius Confidence Bounds|Appendix 6.A]]). | Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure the more distant the accelerated stress from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in [[Appendix A: Brief Statistical Background|Appendix A]]. Specific calculations for confidence bounds on the Arrhenius model are presented in [[Arrhenius Relationship#Appendix 6.A: Arrhenius Confidence Bounds|Appendix 6.A]]). | ||
<br> | <br> | ||
[[Image:ALTA6.10.png|center| | [[Image:ALTA6.10.png|center|500px|Comparison of the confidence bounds for different use stress levels.]] | ||
Revision as of 15:32, 22 June 2012
Arrhenius-Weibull Example
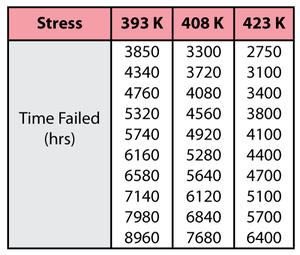
Consider the following times-to-failure data at three different stress levels.
The data set was analyzed jointly and with a complete MLE solution over the entire data set, using ReliaSoft's ALTA. The analysis yields:
- [math]\displaystyle{ \widehat{\beta }=4.2915822 }[/math]
- [math]\displaystyle{ \widehat{B}=1861.6186657 }[/math]
- [math]\displaystyle{ \widehat{C}=58.9848692 }[/math]
Once the parameters of the model are estimated, extrapolation and other life measures can be directly obtained using the appropriate equations. Using the MLE method, confidence bounds for all estimates can be obtained. Note that in the next figure the more distant the accelerated stress from the operating stress, the greater the uncertainty of the extrapolation. The degree of uncertainty is reflected in the confidence bounds. (General theory and calculations for confidence intervals are presented in Appendix A. Specific calculations for confidence bounds on the Arrhenius model are presented in Appendix 6.A).