Contour Plot Example

Life Comparison - Compare Two Designs Using Contour Plot

The following data sets represent the times-to-failure for a product. Certain modifications were made to this product in order to improve its reliability. Reliability engineers are trying to determine whether the improvements were significant in improving the reliability.

[math]\displaystyle{ \overset{\text{Old Design}}{\mathop{\begin{array}{*{35}{l}} \text{2} & \text{2} & \text{3} & \text{4} & \text{6} & \text{9} \\ \text{9} & \text{11} & \text{17} & \text{17} & \text{19} & \text{21} \\ \text{23} & \text{28} & \text{33} & \text{34} & \text{34} & \text{37} \\ \text{38} & \text{40} & \text{45} & \text{55} & \text{56} & \text{57} \\ \text{67} & \text{76} & \text{90} & \text{115} & \text{126} & \text{197} \\ \end{array}}}\, }[/math]

[math]\displaystyle{ \overset{\text{New Design}}{\mathop{\begin{array}{*{35}{l}} \text{15} & \text{32} & \text{61} & \text{67} & \text{75} \\ \text{116} & \text{148} & \text{178} & \text{181} & \text{183} \\ \end{array}}}\, }[/math]

At what significance level can the engineers claim that the two designs are different?

Solution

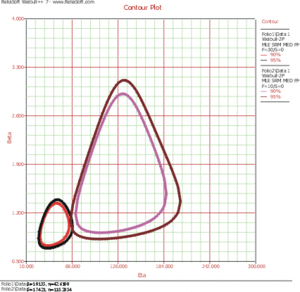
For both data sets, the two-parameter Weibull distribution best fits the data. The contour plots were generated and plotted together on an overlay plot in Weibull++.

[math]\displaystyle{ }[/math]

From this plot, it can be seen that there is an overlap at the 95% confidence level and that there is no overlap at the 90% confidence level. It can then be concluded that the new design is better at the 90% confidence level. If an analyst wanted to know at exactly what confidence the two contour plots meet, she would have to incrementally raise the confidence level from 90% until the two plots met. In fact, this search process has been automated by the Confidence Level Detector utility.