Template:Example: Test Design Using Expected Failure Times Plot: Difference between revisions
Chris Kahn (talk | contribs) No edit summary |
Lisa Hacker (talk | contribs) No edit summary |
||
| Line 6: | Line 6: | ||
'''Solution''' | '''Solution''' | ||
The expected failure | The expected failure times with 80% 2-sided confidence bounds are given below. | ||
[[Image: Expected Failure Plot example Result Summary.png|thumb|center|400px]] | [[Image: Expected Failure Plot example Result Summary.png|thumb|center|400px]] | ||
| Line 13: | Line 13: | ||
From the above results, we can see the upper bound of the last failure is about 955 hours. Therefore, the test probably will last for around 955 hours. | From the above results, we can see the upper bound of the last failure is about 955 hours. Therefore, the test probably will last for around 955 hours. | ||
As we know, with four samples, the median rank for the second failure is 0.385728. Using this value and the assumed Weibull distribution, the median value of the failure time of the | As we know, with four samples, the median rank for the second failure is 0.385728. Using this value and the assumed Weibull distribution, the median value of the failure time of the second failure is calculated as: | ||
<center> | <center> | ||
Revision as of 00:18, 30 March 2012
Test Design Using Expected Failure Times Plot
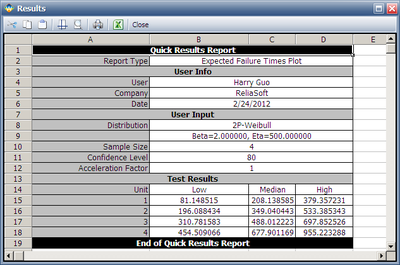
Four units were allocated for a reliability test. The test engineers want to know how long the test will last if all the units are tested to failure. Based on previous experiments, they assume the underlying failure distribution is a Weibull distribution with [math]\displaystyle{ \beta }[/math] = 2 and [math]\displaystyle{ \eta }[/math] = 500.
Solution
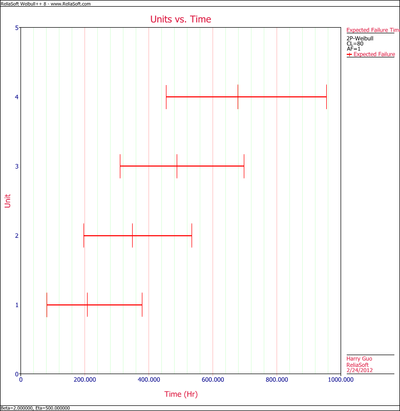
The expected failure times with 80% 2-sided confidence bounds are given below.
From the above results, we can see the upper bound of the last failure is about 955 hours. Therefore, the test probably will last for around 955 hours.
As we know, with four samples, the median rank for the second failure is 0.385728. Using this value and the assumed Weibull distribution, the median value of the failure time of the second failure is calculated as:
[math]\displaystyle{ \begin{align} & Q=1-{{e}^{{{\left( \frac{t}{\eta } \right)}^{\beta }}}}\Rightarrow \\ & \ln (1-Q)={{\left( \frac{t}{\eta } \right)}^{\beta }} \\ & \Rightarrow t=\text{349.04}\\ \end{align} }[/math]
Its bounds and other failure times can be calculated in a similar way.