Template:Arrhenius formulation: Difference between revisions
| Line 41: | Line 41: | ||
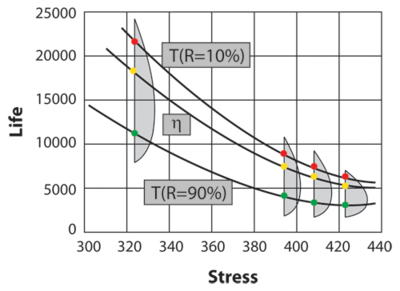
[[Image:ALTA6.1. | [[Image:ALTA6.1.png|center|400px|Graphical look at the Arrhenius life-stress relationship (linear scale) for a different life characteristics, assuming a Weibull distribution.]] | ||
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless. | Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless. | ||
Revision as of 17:48, 23 March 2012
Formulation
The Arrhenius reaction rate equation is given by:
- [math]\displaystyle{ R(T)=A{{e}^{-\tfrac{{{E}_{A}}}{K\cdot T}}} }[/math]
where:
• [math]\displaystyle{ R }[/math] is the speed of reaction.
• [math]\displaystyle{ A }[/math] is an unknown nonthermal constant.
• [math]\displaystyle{ {{E}_{A}} }[/math] is the activation energy ( [math]\displaystyle{ eV }[/math] ).
• [math]\displaystyle{ K }[/math] is the Boltzman's constant ([math]\displaystyle{ 8.617385\times {{10}^{-5}}\text{eV}{{\text{K}}^{-1}}) }[/math]
• [math]\displaystyle{ T }[/math] is the absolute temperature (Kelvin [math]\displaystyle{ ) }[/math] .
The activation energy is the energy that a molecule must have to participate in the reaction. In other words, the activation energy is a measure of the effect that temperature has on the reaction.
The Arrhenius life-stress model is formulated by assuming that life is proportional to the inverse reaction rate of the process, thus the Arrhenius life-stress relationship is given by:
- [math]\displaystyle{ L(V)=C{{e}^{\tfrac{B}{V}}} }[/math]
where:
• [math]\displaystyle{ L }[/math] represents a quantifiable life measure, such as mean life, characteristic life, median life, or [math]\displaystyle{ B(x) }[/math] life, etc.
• [math]\displaystyle{ V }[/math] represents the stress level (formulated for temperature and temperature values in absolute units, degrees Kelvin or degrees Rankine ).
• [math]\displaystyle{ C }[/math] is one of the model parameters to be determined, ( [math]\displaystyle{ C\gt 0). }[/math]
• [math]\displaystyle{ B }[/math] is another model parameter to be determined.
Since the Arrhenius is a physics-based model derived for temperature dependence, it is used for temperature accelerated tests. For the same reason, temperature values must be in absolute units (Kelvin or Rankine), even though the Arrhenius equation is unitless.