Template:ALTA SimuMatic Example: Difference between revisions
No edit summary |
|||
| Line 5: | Line 5: | ||
A reliability engineer wants to design an accelerated test for an electronic component in order to demonstrate a 90% reliability at 1 year with a 90% confidence (1-sided limit). The engineer has 3 months available for testing and wants to determine the required sample size in the test using SimuMatic. The accelerated test will be a temperature test at 350K, 375K and 400K with a use temperature of 300K. The Arrhenius model is chosen as the life vs. stress relationship and the Weibull as the failure distribution. | A reliability engineer wants to design an accelerated test for an electronic component in order to demonstrate a 90% reliability at 1 year with a 90% confidence (1-sided limit). The engineer has 3 months available for testing and wants to determine the required sample size in the test using SimuMatic. The accelerated test will be a temperature test at 350K, 375K and 400K with a use temperature of 300K. The Arrhenius model is chosen as the life vs. stress relationship and the Weibull as the failure distribution. | ||
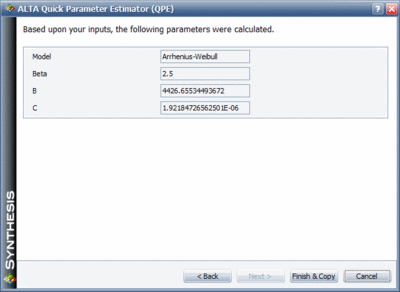
The first thing that needs to be determined in SimuMatic is the parameters of the chosen Arrhenius-Weibull model. | The first thing that needs to be determined in SimuMatic is the parameters of the chosen Arrhenius-Weibull model. Those parameters can be approximated using the Quick Parameter Estimator (QPE) tool in ALTA. Based on historical field information the engineer estimates a beta of 2.5 and a B10 life of 2 years at the use stress of 300K. The next figure shows the QPE with the stated assumptions. | ||
[[image: ALTA_SimuMatic_Example_1.gif|thumb|center|400px]] | |||
The next required input in the QPE is the characteristic life at a higher stress. From past accelerated tests the engineer expects to achieve an acceleration factor of 40 between the highest stress level and the use stress level. Therefore he sets the characteristic life at 400K as 1/40th of the calculated characteristic life at 300K as shown in the next figure. | |||
[[image: ALTA_SimuMatic_Example_2.gif|thumb|center|400px]] | |||
Based on that information the parameters of the Arrhenius-Weibull model can be determined as shown next. | |||
[[image: ALTA_SimuMatic_Example_3.gif|thumb|center|400px]] | |||
Revision as of 22:54, 20 March 2012
SimuMatic Example
SimuMatic is a simulation tool that can assist in designing accelerated tests. The following example illustrates a potential use of SimuMatic.
A reliability engineer wants to design an accelerated test for an electronic component in order to demonstrate a 90% reliability at 1 year with a 90% confidence (1-sided limit). The engineer has 3 months available for testing and wants to determine the required sample size in the test using SimuMatic. The accelerated test will be a temperature test at 350K, 375K and 400K with a use temperature of 300K. The Arrhenius model is chosen as the life vs. stress relationship and the Weibull as the failure distribution.
The first thing that needs to be determined in SimuMatic is the parameters of the chosen Arrhenius-Weibull model. Those parameters can be approximated using the Quick Parameter Estimator (QPE) tool in ALTA. Based on historical field information the engineer estimates a beta of 2.5 and a B10 life of 2 years at the use stress of 300K. The next figure shows the QPE with the stated assumptions.
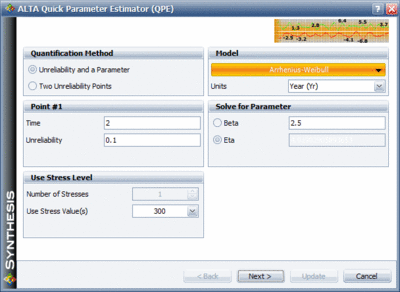
The next required input in the QPE is the characteristic life at a higher stress. From past accelerated tests the engineer expects to achieve an acceleration factor of 40 between the highest stress level and the use stress level. Therefore he sets the characteristic life at 400K as 1/40th of the calculated characteristic life at 300K as shown in the next figure.
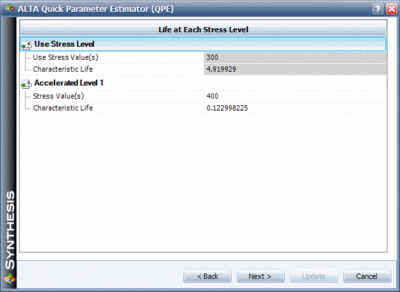
Based on that information the parameters of the Arrhenius-Weibull model can be determined as shown next.