Template:Logistic probability paper: Difference between revisions
| Line 1: | Line 1: | ||
==Logistic Distribution Probability Paper== | ==Logistic Distribution Probability Paper== | ||
The form of the Logistic probability paper is based on linearizing the <math>cdf</math> . | The form of the Logistic probability paper is based on linearizing the <math>cdf</math> . | ||
From unreliability equation, <math>z</math> can be calculated as a function of the <math>cdf</math> <math>F</math> as follows: | From unreliability equation, <math>z</math> can be calculated as a function of the <math>cdf</math> <math>F</math> as follows: | ||
| Line 32: | Line 31: | ||
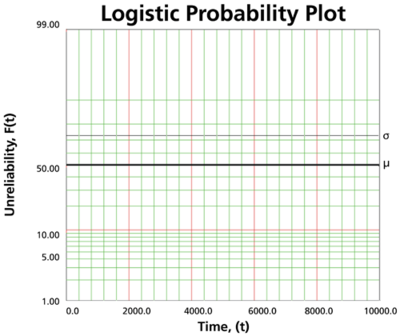
The logistic probability paper resulting from this linearized <math>cdf</math> function is shown next. | The logistic probability paper resulting from this linearized <math>cdf</math> function is shown next. | ||
[[Image: | [[Image:WB.14 logistic probability plot.png|center|400px| ]] | ||
Since the logistic distribution is symmetrical, the area under the <math>pdf</math> curve from <math>-\infty </math> to <math>\mu </math> is <math>0.5</math> , as is the area from <math>\mu </math> to <math>+\infty </math> . Consequently, the value of <math>\mu </math> is said to be the point where <math>R(t)=Q(t)=50%</math> . This means that the estimate of <math>\mu </math> can be read from the point where the plotted line crosses the 50% unreliability line. | Since the logistic distribution is symmetrical, the area under the <math>pdf</math> curve from <math>-\infty </math> to <math>\mu </math> is <math>0.5</math> , as is the area from <math>\mu </math> to <math>+\infty </math> . Consequently, the value of <math>\mu </math> is said to be the point where <math>R(t)=Q(t)=50%</math> . This means that the estimate of <math>\mu </math> can be read from the point where the plotted line crosses the 50% unreliability line. | ||
For <math>z=1</math> , <math>\sigma =t-\mu </math> and <math>R(t)=\tfrac{1}{1+\exp (1)}\approx 0.2689.</math> Therefore, <math>\sigma </math> can be found by subtracting <math>\mu </math> from the time value where the plotted probability line crosses the 73.10% unreliability (26.89% reliability) horizontal line. | For <math>z=1</math> , <math>\sigma =t-\mu </math> and <math>R(t)=\tfrac{1}{1+\exp (1)}\approx 0.2689.</math> Therefore, <math>\sigma </math> can be found by subtracting <math>\mu </math> from the time value where the plotted probability line crosses the 73.10% unreliability (26.89% reliability) horizontal line. | ||
Revision as of 17:32, 15 March 2012
Logistic Distribution Probability Paper
The form of the Logistic probability paper is based on linearizing the [math]\displaystyle{ cdf }[/math] . From unreliability equation, [math]\displaystyle{ z }[/math] can be calculated as a function of the [math]\displaystyle{ cdf }[/math] [math]\displaystyle{ F }[/math] as follows:
- [math]\displaystyle{ z=\ln (F)-\ln (1-F) }[/math]
or using the equation for z
- [math]\displaystyle{ \frac{t-\mu }{\sigma }=\ln (F)-\ln (1-F) }[/math]
Then:
- [math]\displaystyle{ \ln (F)-\ln (1-F)=-\frac{\mu }{\sigma }+\frac{1}{\sigma }t }[/math]
Now let:
- [math]\displaystyle{ y=\ln (F)-\ln (1-F) }[/math]
- [math]\displaystyle{ x=t }[/math]
and:
- [math]\displaystyle{ a=-\frac{\mu }{\sigma } }[/math]
- [math]\displaystyle{ b=\frac{1}{\sigma } }[/math]
which results in the following linear equation:
- [math]\displaystyle{ y=a+bx }[/math]
The logistic probability paper resulting from this linearized [math]\displaystyle{ cdf }[/math] function is shown next.
Since the logistic distribution is symmetrical, the area under the [math]\displaystyle{ pdf }[/math] curve from [math]\displaystyle{ -\infty }[/math] to [math]\displaystyle{ \mu }[/math] is [math]\displaystyle{ 0.5 }[/math] , as is the area from [math]\displaystyle{ \mu }[/math] to [math]\displaystyle{ +\infty }[/math] . Consequently, the value of [math]\displaystyle{ \mu }[/math] is said to be the point where [math]\displaystyle{ R(t)=Q(t)=50% }[/math] . This means that the estimate of [math]\displaystyle{ \mu }[/math] can be read from the point where the plotted line crosses the 50% unreliability line.
For [math]\displaystyle{ z=1 }[/math] , [math]\displaystyle{ \sigma =t-\mu }[/math] and [math]\displaystyle{ R(t)=\tfrac{1}{1+\exp (1)}\approx 0.2689. }[/math] Therefore, [math]\displaystyle{ \sigma }[/math] can be found by subtracting [math]\displaystyle{ \mu }[/math] from the time value where the plotted probability line crosses the 73.10% unreliability (26.89% reliability) horizontal line.