Template:Loglogistic distribution characteristics: Difference between revisions
Jump to navigation
Jump to search
No edit summary |
|||
| Line 17: | Line 17: | ||
:* <math>\lambda (t)</math> increases till <math>t={{e}^{\mu +\sigma \ln (\tfrac{1-\sigma }{\sigma })}}</math> and decreases thereafter. <math>\lambda (t)</math> is concave at first, then becomes convex. | :* <math>\lambda (t)</math> increases till <math>t={{e}^{\mu +\sigma \ln (\tfrac{1-\sigma }{\sigma })}}</math> and decreases thereafter. <math>\lambda (t)</math> is concave at first, then becomes convex. | ||
[[Image: | [[Image:WB.15 loglogistic pdf.png|center|400px| ]] | ||
Revision as of 17:24, 15 March 2012
Distribution Characteristics
For [math]\displaystyle{ \sigma \gt 1 }[/math] :
- [math]\displaystyle{ f(t) }[/math] decreases monotonically and is convex. Mode and mean do not exist.
For [math]\displaystyle{ \sigma =1 }[/math] :
- [math]\displaystyle{ f(t) }[/math] decreases monotonically and is convex. Mode and mean do not exist. As [math]\displaystyle{ t\to 0 }[/math] , [math]\displaystyle{ f(t)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}. }[/math]
- As [math]\displaystyle{ t\to 0 }[/math] , [math]\displaystyle{ \lambda (t)\to \tfrac{1}{\sigma {{e}^{\tfrac{\mu }{\sigma }}}}. }[/math]
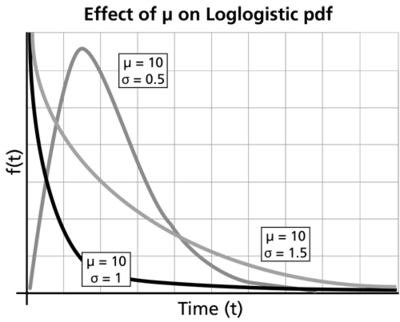
For [math]\displaystyle{ 0\lt \sigma \lt 1 }[/math] :
- The shape of the loglogistic distribution is very similar to that of the lognormal distribution and the Weibull distribution.
- The [math]\displaystyle{ pdf }[/math] starts at zero, increases to its mode, and decreases thereafter.
- As [math]\displaystyle{ \mu }[/math] increases, while [math]\displaystyle{ \sigma }[/math] is kept the same, the [math]\displaystyle{ pdf }[/math] gets stretched out to the right and its height decreases, while maintaining its shape.
- As [math]\displaystyle{ \mu }[/math] decreases,while [math]\displaystyle{ \sigma }[/math] is kept the same, the .. gets pushed in towards the left and its height increases.
- [math]\displaystyle{ \lambda (t) }[/math] increases till [math]\displaystyle{ t={{e}^{\mu +\sigma \ln (\tfrac{1-\sigma }{\sigma })}} }[/math] and decreases thereafter. [math]\displaystyle{ \lambda (t) }[/math] is concave at first, then becomes convex.