Template:Characteristics of the exponential distribution alta: Difference between revisions
Jump to navigation
Jump to search
Chris Kahn (talk | contribs) No edit summary |
|||
| Line 1: | Line 1: | ||
===Characteristics | === Characteristics === | ||
The characteristics of the 1-parameter exponential distribution can be exemplified by examining its parameter, lambda (<span class="texhtml">λ<span style="font-family: sans-serif;">)</span></span> and the effect lambda has on the <span class="texhtml">''p''''d''''f''</span>, reliability and failure rate functions.<br> | |||
The failure rate function for the exponential distribution is constant and it is equal to the parameter | ==== Effects of <span class="texhtml">λ</span> on the ''pdf'' ==== | ||
<br> | |||
[[Image:ALTA4FRvsTP.gif|thumb|center|400px | <br> | ||
<br> | |||
[[Image:ALTA4pdf.gif|thumb|center|400px]] <br> | |||
:*The scale parameter is <math>\tfrac{1}{\lambda }</math> . | |||
:*As <span class="texhtml">λ</span> is decreased in value, the distribution is stretched out to the right, and as <span class="texhtml">λ</span> is increased, the distribution is pushed toward the origin. | |||
:*This distribution has no shape parameter, as it has only one shape (i.e., the exponential). Its only parameter is the failure rate, <span class="texhtml">λ</span> . | |||
:*The distribution starts at <span class="texhtml">''T'' = 0</span> at the level of <span class="texhtml">''f''(''T'' = 0) = λ</span>, and it decreases thereafter exponentially and monotonically as <span class="texhtml">''T''</span> increases. The distribution is convex. | |||
:*As <math>T\to \infty </math> , <math>f(T)\to 0</math>. | |||
:*This ''pdf'' can be thought of as a special case of the Weibull<span class="texhtml"</span> ''pdf'' with <span class="texhtml">β = 1</span>. | |||
<br> [[Image:ALTA4reliabilityvstimeplot.gif|thumb|center|400px]] <br> | |||
==== Effects of <span class="texhtml">λ</span> on the Reliability Function ==== | |||
:*The 1-parameter exponential reliability function starts at the value of 1 at <span class="texhtml">''T'' = 0</span> . It decreases thereafter monotonically and is convex. | |||
:*As <math>T\to \infty </math> , <math>R(T\to \infty )\to 0</math>. | |||
==== Effects of <span class="texhtml">λ</span> on the Failure Rate Function ==== | |||
The failure rate function for the exponential distribution is constant and it is equal to the parameter <span class="texhtml">λ</span> . | |||
<br> [[Image:ALTA4FRvsTP.gif|thumb|center|400px]] <br> | |||
Revision as of 22:39, 6 March 2012
Characteristics
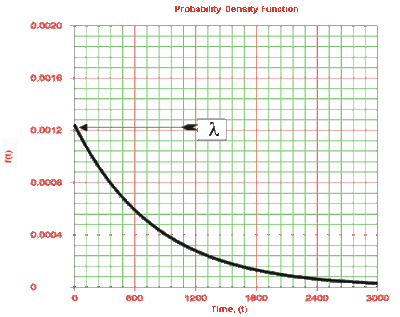
The characteristics of the 1-parameter exponential distribution can be exemplified by examining its parameter, lambda (λ) and the effect lambda has on the p'd'f, reliability and failure rate functions.
Effects of λ on the pdf
- The scale parameter is [math]\displaystyle{ \tfrac{1}{\lambda } }[/math] .
- As λ is decreased in value, the distribution is stretched out to the right, and as λ is increased, the distribution is pushed toward the origin.
- This distribution has no shape parameter, as it has only one shape (i.e., the exponential). Its only parameter is the failure rate, λ .
- The distribution starts at T = 0 at the level of f(T = 0) = λ, and it decreases thereafter exponentially and monotonically as T increases. The distribution is convex.
- As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ f(T)\to 0 }[/math].
- This pdf can be thought of as a special case of the Weibull<span class="texhtml"</span> pdf with β = 1.
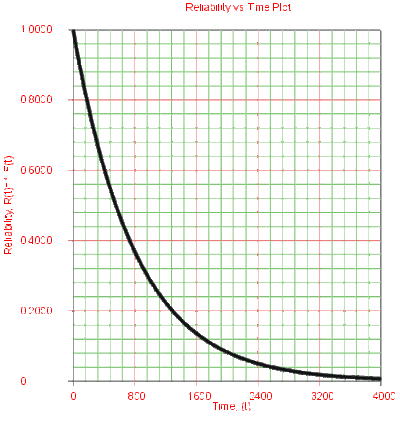
Effects of λ on the Reliability Function
- The 1-parameter exponential reliability function starts at the value of 1 at T = 0 . It decreases thereafter monotonically and is convex.
- As [math]\displaystyle{ T\to \infty }[/math] , [math]\displaystyle{ R(T\to \infty )\to 0 }[/math].
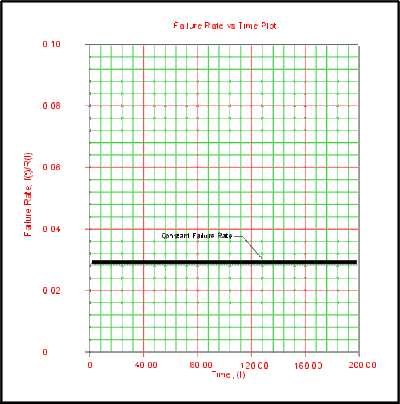
Effects of λ on the Failure Rate Function
The failure rate function for the exponential distribution is constant and it is equal to the parameter λ .