Template:Example: 2P Weibull Distribution RRY: Difference between revisions
No edit summary |
No edit summary |
||
| Line 89: | Line 89: | ||
Also, so that you get the same results as this example, switch to the ''Analysis'' page and make sure you are using the ''Rank Regression on Y (RRY)'' calculation method with this example, as shown next. | Also, so that you get the same results as this example, switch to the ''Analysis'' page and make sure you are using the ''Rank Regression on Y (RRY)'' calculation method with this example, as shown next. | ||
[[Image: | [[Image:Weibull Distribution Example 3 Select RRY.png|thumb|center|400px| ]] | ||
Note that this can also be done from the ''Main'' page by clicking the left bottom box under the Results area. Each time you click that box you will see the method switch between MLE, RRX, and RRY. Click the ''Calculate'' icon, | Note that this can also be done from the ''Main'' page by clicking the left bottom box under the Results area. Each time you click that box you will see the method switch between MLE, RRX, and RRY. Click the ''Calculate'' icon, | ||
| Line 97: | Line 97: | ||
or select ''Calculate'' from the ''Data'' menu. The results will appear in the Data Folio's ''Results area''. The next figure shows the results for this example. | or select ''Calculate'' from the ''Data'' menu. The results will appear in the Data Folio's ''Results area''. The next figure shows the results for this example. | ||
[[Image: | [[Image:Weibull Distribution Example 3 RRY Result.png|thumb|center|400px| ]] | ||
<br> | <br> | ||
| Line 107: | Line 107: | ||
The Weibull probability plot for these data is shown next. | The Weibull probability plot for these data is shown next. | ||
[[Image: Weibull Distribution Example 3 RRY Plot.pngthumb|center|400px|]] | |||
The confidence bounds, as determined from the Fisher matrix, can also be plotted. Select ''Confidence Bounds'' from the ''Plot'' menu, choose ''Two-Sided'' under ''Sides,'' ''Reliability (Type II)'' under ''Type'' and enter ''90'' for the ''Confidence level. | The confidence bounds, as determined from the Fisher matrix, can also be plotted. Select ''Confidence Bounds'' from the ''Plot'' menu, choose ''Two-Sided'' under ''Sides,'' ''Reliability (Type II)'' under ''Type'' and enter ''90'' for the ''Confidence level. | ||
[[Image:weibullconfidencebounds.png|thumb|center|400px| ]] | [[Image:weibullconfidencebounds.png|thumb|center|400px| ]] | ||
| Line 116: | Line 117: | ||
The plot will appear as follows, | The plot will appear as follows, | ||
[[Image: | [[Image:Weibull Distribution Example 3 RRY Confidence Plot.png|thumb|center|400px| ]] | ||
If desired, the Weibull <math>pdf</math> representing these data can be written as: | If desired, the Weibull <math>pdf</math> representing these data can be written as: | ||
| Line 128: | Line 129: | ||
You can also plot the Weibull by selecting ''Pdf Plot'' from the ''Plot Type'' drop-down menu on the control panel to the right of the plot area. | You can also plot the Weibull by selecting ''Pdf Plot'' from the ''Plot Type'' drop-down menu on the control panel to the right of the plot area. | ||
[[Image: | [[Image:Weibull Distribution Example 3 pdf Plot.png|thumb|center|400px]] | ||
From this point on, different results, reports and plots can be obtained. | From this point on, different results, reports and plots can be obtained. | ||
Revision as of 22:39, 1 March 2012
2P Weibull Distribution RRY Example
Consider the data in Example 1, where six units were tested to failure and the following failure times were recorded: 16, 34, 53, 75, 93 and 120 hours. Estimate the parameters and the correlation coefficient using rank regression on Y, assuming that the data follow the two-parameter Weibull distribution.
Solution
Construct a table as shown below.
| Table - Least Squares Analysis | |||||||
| [math]\displaystyle{ N }[/math] | [math]\displaystyle{ T_{i} }[/math] | [math]\displaystyle{ ln(T_{i}) }[/math] | [math]\displaystyle{ F(T_i) }[/math] | [math]\displaystyle{ y_{i} }[/math] | [math]\displaystyle{ (ln{T_i})^2 }[/math] | [math]\displaystyle{ {y_i}^2 }[/math] | [math]\displaystyle{ (ln{T_i})y_i }[/math] |
|---|---|---|---|---|---|---|---|
| 1 | 16 | 2.7726 | 0.1091 | -2.1583 | 7.6873 | 4.6582 | -5.9840 |
| 2 | 34 | 3.5264 | 0.2645 | -1.1802 | 12.4352 | 1.393 | -4.1620 |
| 3 | 53 | 3.9703 | 0.4214 | -0.6030 | 15.7632 | 0.3637 | -2.3943 |
| 4 | 75 | 4.3175 | 0.5786 | -0.146 | 18.6407 | 0.0213 | -0.6303 |
| 5 | 93 | 4.5326 | 0.7355 | 0.2851 | 20.5445 | 0.0813 | 1.2923 |
| 6 | 120 | 4.7875 | 0.8909 | 0.7955 | 22.9201 | 0.6328 | 3.8083 |
| [math]\displaystyle{ \sum }[/math] | 23.9068 | -3.007 | 97.9909 | 7.1502 | -8.0699 | ||
Utilizing the values from above table, calculate [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{b} }[/math] using the following equations:
- [math]\displaystyle{ \hat{b} =\frac{\sum\limits_{i=1}^{6}(\ln t_{i})y_{i}-(\sum\limits_{i=1}^{6}\ln t_{i})(\sum\limits_{i=1}^{6}y_{i})/6}{ \sum\limits_{i=1}^{6}(\ln t_{i})^{2}-(\sum\limits_{i=1}^{6}\ln t_{i})^{2}/6} }[/math]
- [math]\displaystyle{ \hat{b}=\frac{-8.0699-(23.9068)(-3.0070)/6}{97.9909-(23.9068)^{2}/6} }[/math]
or
- [math]\displaystyle{ \hat{b}=1.4301 }[/math]
and:
- [math]\displaystyle{ \hat{a}=\overline{y}-\hat{b}\overline{T}=\frac{\sum \limits_{i=1}^{N}y_{i}}{N}-\hat{b}\frac{\sum\limits_{i=1}^{N}\ln t_{i}}{N } }[/math]
or:
- [math]\displaystyle{ \hat{a}=\frac{(-3.0070)}{6}-(1.4301)\frac{23.9068}{6}=-6.19935 }[/math]
Therefore:
- [math]\displaystyle{ \hat{\beta }=\hat{b}=1.4301 }[/math]
and:
- [math]\displaystyle{ \hat{\eta }=e^{-\frac{\hat{a}}{\hat{b}}}=e^{-\frac{(-6.19935)}{ 1.4301}} }[/math]
or:
- [math]\displaystyle{ \hat{\eta }=76.318\text{ hr} }[/math]
The correlation coefficient can be estimated as:
- [math]\displaystyle{ \hat{\rho }=0.9956 }[/math]
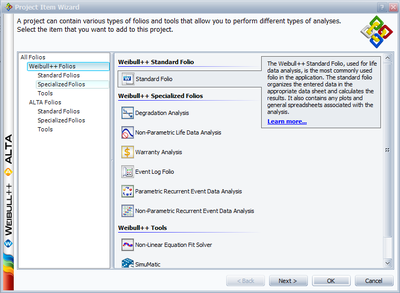
The above example can be repeated using Weibull++. Start Weibull++ and create a new Data Folio.
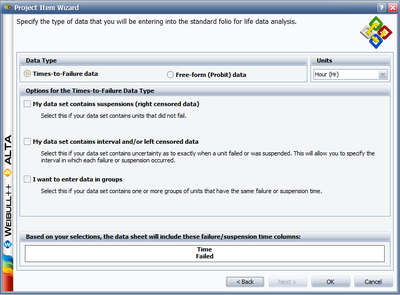
Select the Times-to-failure data option.
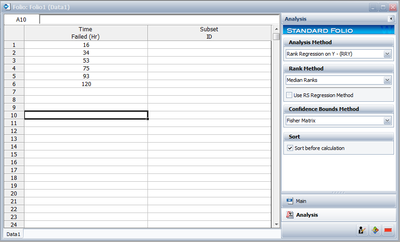
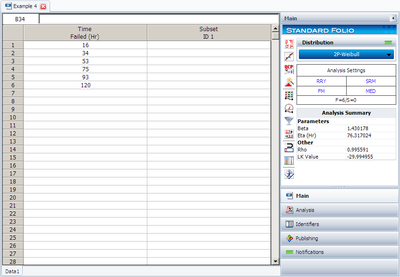
Enter the times-to-failure in the datasheet (ignore the Subset ID column), as shown next. The times-to-failure need not be sorted, Weibull++ will automatically sort the data.
Select the desired method of analysis. Note that we are assuming that the underlying distribution is the Weibull, so make sure that the 2P-Weibull distribution is selected.
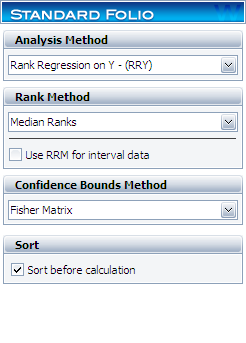
Also, so that you get the same results as this example, switch to the Analysis page and make sure you are using the Rank Regression on Y (RRY) calculation method with this example, as shown next.
Note that this can also be done from the Main page by clicking the left bottom box under the Results area. Each time you click that box you will see the method switch between MLE, RRX, and RRY. Click the Calculate icon,
or select Calculate from the Data menu. The results will appear in the Data Folio's Results area. The next figure shows the results for this example.
You can now plot the results by clicking the Plot icon,
or by selecting Plot Probability from the Data menu.
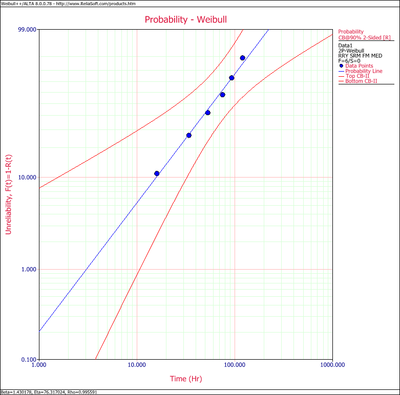
The Weibull probability plot for these data is shown next.
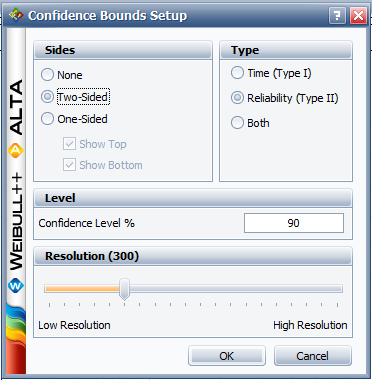
The confidence bounds, as determined from the Fisher matrix, can also be plotted. Select Confidence Bounds from the Plot menu, choose Two-Sided under Sides, Reliability (Type II) under Type and enter 90 for the Confidence level.
The plot will appear as follows,
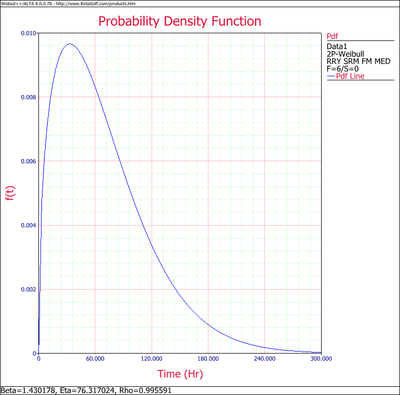
If desired, the Weibull [math]\displaystyle{ pdf }[/math] representing these data can be written as:
- [math]\displaystyle{ f(t)={\frac{\beta }{\eta }}\left( {\frac{t}{\eta }}\right) ^{\beta -1}e^{-\left( {\frac{t}{\eta }}\right) ^{\beta }} }[/math]
or:
- [math]\displaystyle{ f(t)={\frac{1.4302}{76.317}}\left( {\frac{t}{76.317}}\right) ^{0.4302}e^{-\left( {\frac{t}{76.317}}\right) ^{1.4302}} }[/math]
You can also plot the Weibull by selecting Pdf Plot from the Plot Type drop-down menu on the control panel to the right of the plot area.
From this point on, different results, reports and plots can be obtained.