Template:Example: Weibull Distribution Suspension Data Example

Weibull Distribution Suspension Data Example

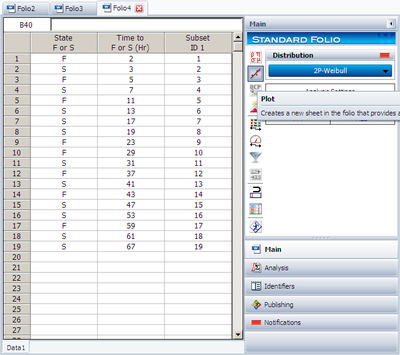
ACME company manufactures widgets, and is currently engaged in reliability testing a new widget design. Nineteen units are being reliability tested, but due to the tremendous demand for widgets, units are removed from the test whenever the production cannot cover the demand. The test is terminated at the 67th day when the last widget is removed from the test. Table 6.6 contains the collected data.

Widget Test Data

Data Point Index	Last Inspection	Time to Failure
1	F	2
2	S	3
3	F	5
4	S	7
5	F	11
6	S	13
7	S	17
8	S	19
9	F	23
10	F	29
11	S	31
12	F	37
13	S	41
14	F	43
15	S	47
16	S	53
17	F	59
18	S	61
19	S	67

Solution

In this example, we see that the number of failures is less than the number of suspensions. This is a very common situation, since reliability tests are often terminated before all units fail due to financial or time constraints. Further, some suspensions will be recorded when a failure occurs that is not due to a legitimate failure mode, such as operator error. In cases such as this, a suspension is recorded, since the unit under test cannot be said to have had a legitimate failure.

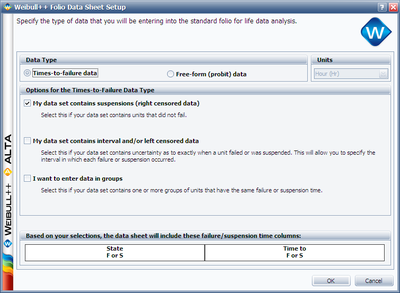
This data set can be entered into Weibull++ using Times-to-failure and My data set contains suspensions (right censored data).

After enter the data, the data folio looks like:

We will use the two-parameter Weibull to solve this problem. The parameters using maximum likelihood are:

[math]\displaystyle{ \begin{align} & \hat{\beta }=1.145 \\ & \hat{\eta }=65.97 \\ \end{align} }[/math]

using RRX:

[math]\displaystyle{ \begin{align} & \hat{\beta }=0.914\\ & \hat{\eta }=79.38 \\ \end{align} }[/math]

and using RRY:

[math]\displaystyle{ \begin{align} & \hat{\beta }=0.895\\ & \hat{\eta }=82.02 \\ \end{align} }[/math]