Template:Difference detection matrix: Difference between revisions
No edit summary |
|||
| Line 1: | Line 1: | ||
==Test Design Using Life Difference Detection Matrix== | ==Test Design Using Life Difference Detection Matrix== | ||
Engineers often need to design tests for detecting life differences between two or more product designs. The questions are how many samples and how long the test should be conducted in order to detect a certain amount of difference. There are no simple answers. Usually, advanced design of experiments (DOE) techiques should be utilized. For simple case, such as comparing two designs, the Difference Detection Matrix in Weibull++ can be used. The difference detection matrix graphically indicates the amount of test time required to detect a statistical difference in the lives of two populations. | |||
As discussed in the test design using expected failure times plot, if the sample size is known, the expected failure time of each test unit can be obtained based on the assumed failure distribution. Now let's go one step further. With these failure times, we can then estimate the failure distribution and calculate any reliability metrics. This process is similar to the simulation used in [[Weibull SimuMatic|Simumatic]] where random failure times are generated from simulation and then used to estimate the failure distribution. This is also used by the difference detection matrix. | |||
Assume we want to compare the B10 lives of two designs. The test is time terminated and the terimation time is set to ''T''. Using the method given in section [[Test Design Using Expected Failure Time Plots]], we can generate the failure times. For any failure time greater than ''T'', it is a suspension and the suspension time is ''T''. For each design, it B10 life and confidence bounds can be estimated from the generated failure/suspension times. If the two confidence intervals of the two designs overlap with each other, | |||
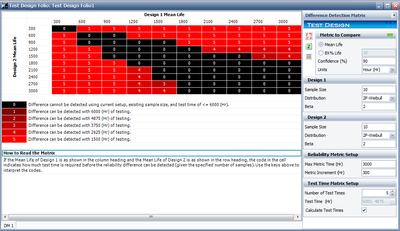
The Difference Detection Matrix takes as inputs information about the samples and information about the testing setup. For each sample, the Difference Detection Matrix needs the size of the sample, the distribution to be assumed for the sample population’s life, and a parameter affecting the variance of each population’s life distribution (e.g., beta for Weibull, and sigma for Normal and Lognormal). The Difference Detection Matrix also needs to know what the maximum allowable test time is, and by what amount of time to increment to the mean lives to be compared. For example, in the design shown below, the mean lives are incremented by 300, up to a mean life of 3000. | The Difference Detection Matrix takes as inputs information about the samples and information about the testing setup. For each sample, the Difference Detection Matrix needs the size of the sample, the distribution to be assumed for the sample population’s life, and a parameter affecting the variance of each population’s life distribution (e.g., beta for Weibull, and sigma for Normal and Lognormal). The Difference Detection Matrix also needs to know what the maximum allowable test time is, and by what amount of time to increment to the mean lives to be compared. For example, in the design shown below, the mean lives are incremented by 300, up to a mean life of 3000. | ||
Revision as of 18:28, 24 February 2012
Test Design Using Life Difference Detection Matrix
Engineers often need to design tests for detecting life differences between two or more product designs. The questions are how many samples and how long the test should be conducted in order to detect a certain amount of difference. There are no simple answers. Usually, advanced design of experiments (DOE) techiques should be utilized. For simple case, such as comparing two designs, the Difference Detection Matrix in Weibull++ can be used. The difference detection matrix graphically indicates the amount of test time required to detect a statistical difference in the lives of two populations.
As discussed in the test design using expected failure times plot, if the sample size is known, the expected failure time of each test unit can be obtained based on the assumed failure distribution. Now let's go one step further. With these failure times, we can then estimate the failure distribution and calculate any reliability metrics. This process is similar to the simulation used in Simumatic where random failure times are generated from simulation and then used to estimate the failure distribution. This is also used by the difference detection matrix.
Assume we want to compare the B10 lives of two designs. The test is time terminated and the terimation time is set to T. Using the method given in section Test Design Using Expected Failure Time Plots, we can generate the failure times. For any failure time greater than T, it is a suspension and the suspension time is T. For each design, it B10 life and confidence bounds can be estimated from the generated failure/suspension times. If the two confidence intervals of the two designs overlap with each other,
The Difference Detection Matrix takes as inputs information about the samples and information about the testing setup. For each sample, the Difference Detection Matrix needs the size of the sample, the distribution to be assumed for the sample population’s life, and a parameter affecting the variance of each population’s life distribution (e.g., beta for Weibull, and sigma for Normal and Lognormal). The Difference Detection Matrix also needs to know what the maximum allowable test time is, and by what amount of time to increment to the mean lives to be compared. For example, in the design shown below, the mean lives are incremented by 300, up to a mean life of 3000.
The last thing the Difference Detection Matrix needs is what amounts of testing are available. The lengths of testing are initialized automatically, but can easily be modified by simply clicking on the pulldown menu and entering the time desired. When you are ready to calculate new values, just press the calculate icon in the right-hand panel.
After matrix values have been calculated, their codes can be interpreted using the legend below the matrix. The legend shows what level of testing corresponds to each color and code. In the figure shown above, a mean life of design 1 of 900 hours can be told from a mean life of design 2 of 1800 hours after 1500 hours of testing (code 3). A black cell indicates that a statistically significant difference between the two populations’ mean lives cannot be detected with the resources available, either due to insufficient sample sizes or inadequate test time.