Template:Example: Exponential Distribution Demonstration Test Example: Difference between revisions
No edit summary |
No edit summary |
||
| Line 14: | Line 14: | ||
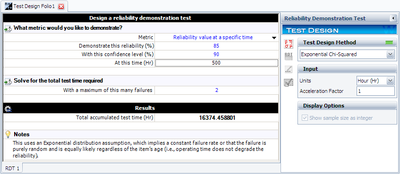
This example solved in Weibull++ is shown next. | This example solved in Weibull++ is shown next. | ||
[[Image: Test Design Chi-Squared.png|thumb|center]] | [[Image: Test Design Chi-Squared.png|thumb|center|400px]] | ||
Given the test time, one can now solve for the number of units using the Chi-Squared equation. Similarly, if the number of units is given, one can determine the test time from the Chi-Squared equation for exponential test design. | Given the test time, one can now solve for the number of units using the Chi-Squared equation. Similarly, if the number of units is given, one can determine the test time from the Chi-Squared equation for exponential test design. | ||
Revision as of 19:10, 23 February 2012
Exponential Distribution Demonstration Test Example
In this example, we desire to design a test to demonstrate a reliability of 85% at [math]\displaystyle{ {{t}_{DEMO}}=500 }[/math] hours with a 90% confidence, or [math]\displaystyle{ CL=0.9, }[/math] and two allowable failures, [math]\displaystyle{ f=2 }[/math] . The chi-squared value can be determined from tables or the Quick Statistical Reference in Weibull++. In this example, the value is calculated as:
- [math]\displaystyle{ \chi _{1-CL;2r+2}^{2}=\chi _{0.1;6}^{2}=10.6446 }[/math]
Substituting this into the Chi-Squared equation, we obtain:
- [math]\displaystyle{ {{T}_{a}}=\frac{\tfrac{500}{-ln(0.85)}\cdot 10.6446}{2}=16,374\text{ hours} }[/math]
This means that 16,374 hours of total test time need to be accumulated with two failures in order to demonstrate the specified reliability.
This example solved in Weibull++ is shown next.
Given the test time, one can now solve for the number of units using the Chi-Squared equation. Similarly, if the number of units is given, one can determine the test time from the Chi-Squared equation for exponential test design.