Template:Characteristics of the gumbel distribution: Difference between revisions
Jump to navigation
Jump to search
(Created page with '===Characteristics of the Gumbel Distribution=== Some of the specific characteristics of the Gumbel distribution are the following: :• The shape of the Gumbel distribution is …') |
No edit summary |
||
| Line 1: | Line 1: | ||
==Characteristics of the Gumbel Distribution== | |||
Some of the specific characteristics of the Gumbel distribution are the following: | Some of the specific characteristics of the Gumbel distribution are the following: | ||
Revision as of 18:07, 20 February 2012
Characteristics of the Gumbel Distribution
Some of the specific characteristics of the Gumbel distribution are the following:
- • The shape of the Gumbel distribution is skewed to the left. The Gumbel [math]\displaystyle{ pdf }[/math] has no shape parameter. This means that the Gumbel [math]\displaystyle{ pdf }[/math] has only one shape, which does not change.
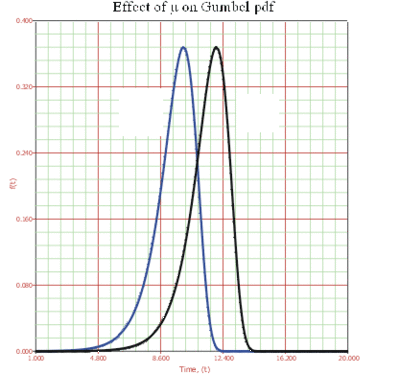
- • The Gumbel [math]\displaystyle{ pdf }[/math] has location parameter [math]\displaystyle{ \mu , }[/math] which is equal to the mode [math]\displaystyle{ \tilde{T}, }[/math] but it differs from median and mean. This is because the Gumbel distribution is not symmetrical about its [math]\displaystyle{ \mu }[/math] .
- • As [math]\displaystyle{ \mu }[/math] decreases, the [math]\displaystyle{ pdf }[/math] is shifted to the left.
- • As [math]\displaystyle{ \mu }[/math] increases, the [math]\displaystyle{ pdf }[/math] is shifted to the right.
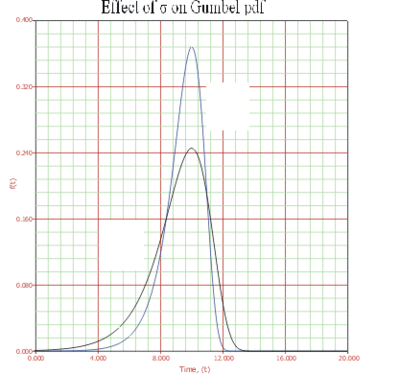
- • As [math]\displaystyle{ \sigma }[/math] increases, the [math]\displaystyle{ pdf }[/math] spreads out and becomes shallower.
- • As [math]\displaystyle{ \sigma }[/math] decreases, the [math]\displaystyle{ pdf }[/math] becomes taller and narrower.
- • For [math]\displaystyle{ T=\pm \infty , }[/math] [math]\displaystyle{ pdf=0. }[/math] For [math]\displaystyle{ T=\mu }[/math] , the [math]\displaystyle{ pdf }[/math] reaches its maximum point [math]\displaystyle{ \frac{1}{\sigma e} }[/math]
- • The points of inflection of the [math]\displaystyle{ pdf }[/math] graph are [math]\displaystyle{ T=\mu \pm \sigma \ln (\tfrac{3\pm \sqrt{5}}{2}) }[/math] or [math]\displaystyle{ T\approx \mu \pm \sigma 0.96242 }[/math] .
- • If times follow the Weibull distribution, then the logarithm of times follow a Gumbel distribution. If [math]\displaystyle{ {{t}_{i}} }[/math] follows a Weibull distribution with [math]\displaystyle{ \beta }[/math] and [math]\displaystyle{ \eta }[/math] , then the [math]\displaystyle{ Ln({{t}_{i}}) }[/math] follows a Gumbel distribution with [math]\displaystyle{ \mu =\ln (\eta ) }[/math] and [math]\displaystyle{ \sigma =\tfrac{1}{\beta } }[/math] [32] [math]\displaystyle{ . }[/math]