Template:Example: Normal Distribution Likelihood Ratio Bound (Time): Difference between revisions
(Created page with ''''Normal Distribution Likelihood Ratio Bound Example (Time)''' For the data given in Example 5, determine the two-sided 80% confidence bounds on the time estimate for a reliabi…') |
No edit summary |
||
| Line 5: | Line 5: | ||
'''Solution''' | '''Solution''' | ||
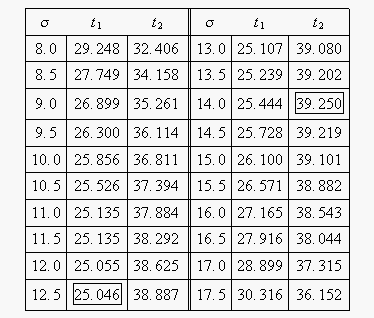
In this example, we are trying to determine the two-sided 80% confidence bounds on the time estimate of 31.637. This is accomplished by substituting <math>R=0.40</math> and <math>\alpha =0.8</math> into | In this example, we are trying to determine the two-sided 80% confidence bounds on the time estimate of 31.637. This is accomplished by substituting <math>R=0.40</math> and <math>\alpha =0.8</math> into the likelihood ratio equation for the normal distribution, and varying <math>\sigma </math> until the maximum and minimum values of <math>t</math> are found. The following table gives the values of <math>t</math> based on given values of <math>\sigma </math> . | ||
[[Image:tabletbasedonsigma.gif|thumb|center|400px| ]] | [[Image:tabletbasedonsigma.gif|thumb|center|400px| ]] | ||
Revision as of 22:18, 10 February 2012
Normal Distribution Likelihood Ratio Bound Example (Time)
For the data given in Example 5, determine the two-sided 80% confidence bounds on the time estimate for a reliability of 40%. The ML estimate for the time at [math]\displaystyle{ R(t)=40% }[/math] is 31.637.
Solution
In this example, we are trying to determine the two-sided 80% confidence bounds on the time estimate of 31.637. This is accomplished by substituting [math]\displaystyle{ R=0.40 }[/math] and [math]\displaystyle{ \alpha =0.8 }[/math] into the likelihood ratio equation for the normal distribution, and varying [math]\displaystyle{ \sigma }[/math] until the maximum and minimum values of [math]\displaystyle{ t }[/math] are found. The following table gives the values of [math]\displaystyle{ t }[/math] based on given values of [math]\displaystyle{ \sigma }[/math] .
[math]\displaystyle{ }[/math]
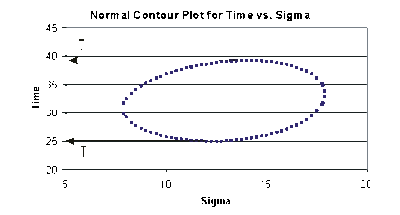
This data set is represented graphically in the following contour plot:
As can be determined from the table, the lowest calculated value for [math]\displaystyle{ t }[/math] is 25.046, while the highest is 39.250. These represent the 80% confidence limits on the time at which reliability is equal to 40%.