Template:Example: Normal Distribution MLE: Difference between revisions
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\frac{\partial \Lambda }{\partial \mu }= & \frac{1}{{{\sigma }^{2}}}\underset{i=1}{\overset{14}{\mathop \sum }}\,({{ | \frac{\partial \Lambda }{\partial \mu }= & \frac{1}{{{\sigma }^{2}}}\underset{i=1}{\overset{14}{\mathop \sum }}\,({{t}_{i}}-\mu )=0 \\ | ||
\frac{\partial \Lambda }{\partial \sigma }= & \underset{i=1}{\overset{14}{\mathop \sum }}\,\left( \frac{{{ | \frac{\partial \Lambda }{\partial \sigma }= & \underset{i=1}{\overset{14}{\mathop \sum }}\,\left( \frac{{{t}_{i}}-\mu }{{{\sigma }^{3}}}-\frac{1}{\sigma } \right)=0 | ||
\end{align}</math> | \end{align}</math> | ||
(The derivations of these equations are presented in [[Appendix: Distribution Log-Likelihood Equations|Appendix]].) Substituting the values of <math>{{ | (The derivations of these equations are presented in [[Appendix: Distribution Log-Likelihood Equations|Appendix]].) Substituting the values of <math>{{t}_{i}}</math> and solving the above system simultaneously, we get <math>\widehat{\sigma }=29.58</math> hours <math>,</math> <math>\widehat{\mu }=45</math> hours <math>.</math> | ||
The Fisher matrix is: | The Fisher matrix is: | ||
| Line 24: | Line 24: | ||
\end{matrix} \right]</math> | \end{matrix} \right]</math> | ||
Using Weibull++ , the MLE method can be selected from the Set Analysis page. | Using Weibull++ , the MLE method can be selected from the Set Analysis page. | ||
| Line 35: | Line 35: | ||
'''Special Note About Bias''' | '''Special Note About Bias''' | ||
Estimators (i.e. parameter estimates) have properties such as unbiasedness, minimum variance, sufficiency, consistency, squared error constancy, efficiency and completeness [7][5]. Numerous books and papers deal with these properties and this coverage is beyond the scope of this reference. | Estimators (i.e. parameter estimates) have properties such as unbiasedness, minimum variance, sufficiency, consistency, squared error constancy, efficiency and completeness [[Appendix: Weibull References|[7][5]]]. Numerous books and papers deal with these properties and this coverage is beyond the scope of this reference. | ||
However, we would like to briefly address one of these properties, unbiasedness. An estimator is said to be unbiased if the estimator <math>\widehat{\theta }=d({{X}_{1,}}{{X}_{2,}}...,{{X}_{n)}}</math> satisfies the condition <math>E\left[ \widehat{\theta } \right]</math> <math>=\theta </math> for all <math>\theta \in \Omega .</math> | However, we would like to briefly address one of these properties, unbiasedness. An estimator is said to be unbiased if the estimator <math>\widehat{\theta }=d({{X}_{1,}}{{X}_{2,}}...,{{X}_{n)}}</math> satisfies the condition <math>E\left[ \widehat{\theta } \right]</math> <math>=\theta </math> for all <math>\theta \in \Omega .</math> | ||
Note that <math>E\left[ X \right]</math> denotes the expected value of X and is defined (for continuous distributions) by: | Note that <math>E\left[ X \right]</math> denotes the expected value of X and is defined (for continuous distributions) by: | ||
| Line 46: | Line 47: | ||
It can be shown [7][5] that the MLE estimator for the mean of the normal (and lognormal) distribution does satisfy the unbiasedness criteria, or <math>E\left[ \widehat{\mu } \right]</math> <math>=\mu .</math> The same is not true for the estimate of the variance <math>\hat{\sigma | It can be shown [[Appendix: Weibull References|[7][5]]] that the MLE estimator for the mean of the normal (and lognormal) distribution does satisfy the unbiasedness criteria, or <math>E\left[ \widehat{\mu } \right]</math> <math>=\mu .</math> The same is not true for the estimate of the variance <math>\hat{\sigma }^{2}</math> . The maximum likelihood estimate for the variance for the normal distribution is given by: | ||
::<math>\hat{\sigma | ::<math>\hat{\sigma }^{2}=\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}}</math> | ||
with a standard deviation of: | with a standard deviation of: | ||
::<math>{{\hat{\sigma } | ::<math>{{\hat{\sigma }}}=\sqrt{\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}}}</math> | ||
These estimates, however, have been shown to be biased. It can be shown [7][5] that the unbiased estimate of the variance and standard deviation for complete data is given by: | These estimates, however, have been shown to be biased. It can be shown [[Appendix: Weibull References|[7][5]]] that the unbiased estimate of the variance and standard deviation for complete data is given by: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\hat{\sigma | \hat{\sigma }^{2}= & \left[ \frac{N}{N-1} \right]\cdot \left[ \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}} \right]=\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}} \\ | ||
{{{\hat{\sigma }} | {{{\hat{\sigma }}}}= & \sqrt{\left[ \frac{N}{N-1} \right]\cdot \left[ \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}} \right]} \\ | ||
= & \sqrt{\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{ | = & \sqrt{\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}}} | ||
\end{align}</math> | \end{align}</math> | ||
| Line 67: | Line 68: | ||
Note that for larger values of <math>N</math> , <math>\sqrt{\left[ N/(N-1) \right]}</math> tends to 1. | Note that for larger values of <math>N</math> , <math>\sqrt{\left[ N/(N-1) \right]}</math> tends to 1. | ||
Weibull++ by default returns the standard deviation | Weibull++ by default returns the unbiased standard deviation given above. | ||
The Use Unbiased Std on Normal Data option in the User Setup under the Calculations tab allows biasing to be considered when estimating the parameters. | The Use Unbiased Std on Normal Data option in the User Setup under the Calculations tab allows biasing to be considered when estimating the parameters. | ||
When this option is selected, Weibull++ returns the standard deviation as defined | When this option is selected, Weibull++ returns the unbiased standard deviation as defined. This is only true for complete data sets. For all other data types, Weibull++ by default returns the standard deviation as defined by Eqn. (normbias2) regardless of the selection status of this option. The next figure shows this setting in Weibull++. | ||
<math></math> | <math></math> | ||
[[Image:ldachp8fig3.gif|thumb|center|300px| ]] | [[Image:ldachp8fig3.gif|thumb|center|300px| ]] | ||
Revision as of 19:15, 10 February 2012
Normal Distribution MLE Example
Using the data of Example 2 and assuming a normal distribution, estimate the parameters using the MLE method.
Solution
In this example we have non-grouped data without suspensions and without interval data. The partial derivatives of the normal log-likelihood function, [math]\displaystyle{ \Lambda , }[/math] are given by:
- [math]\displaystyle{ \begin{align} \frac{\partial \Lambda }{\partial \mu }= & \frac{1}{{{\sigma }^{2}}}\underset{i=1}{\overset{14}{\mathop \sum }}\,({{t}_{i}}-\mu )=0 \\ \frac{\partial \Lambda }{\partial \sigma }= & \underset{i=1}{\overset{14}{\mathop \sum }}\,\left( \frac{{{t}_{i}}-\mu }{{{\sigma }^{3}}}-\frac{1}{\sigma } \right)=0 \end{align} }[/math]
(The derivations of these equations are presented in Appendix.) Substituting the values of [math]\displaystyle{ {{t}_{i}} }[/math] and solving the above system simultaneously, we get [math]\displaystyle{ \widehat{\sigma }=29.58 }[/math] hours [math]\displaystyle{ , }[/math] [math]\displaystyle{ \widehat{\mu }=45 }[/math] hours [math]\displaystyle{ . }[/math]
The Fisher matrix is:
- [math]\displaystyle{ \left[ \begin{matrix} \widehat{Var}\left( \widehat{\mu } \right)=62.5000 & {} & \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right)=0.0000 \\ {} & {} & {} \\ \widehat{Cov}\left( \widehat{\mu },\widehat{\sigma } \right)=0.0000 & {} & \widehat{Var}\left( \widehat{\sigma } \right)=31.2500 \\ \end{matrix} \right] }[/math]
Using Weibull++ , the MLE method can be selected from the Set Analysis page.
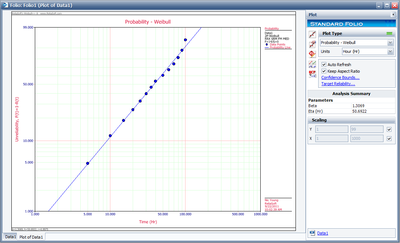
The plot of the solution for this example is shown next.
Special Note About Bias
Estimators (i.e. parameter estimates) have properties such as unbiasedness, minimum variance, sufficiency, consistency, squared error constancy, efficiency and completeness [7][5]. Numerous books and papers deal with these properties and this coverage is beyond the scope of this reference.
However, we would like to briefly address one of these properties, unbiasedness. An estimator is said to be unbiased if the estimator [math]\displaystyle{ \widehat{\theta }=d({{X}_{1,}}{{X}_{2,}}...,{{X}_{n)}} }[/math] satisfies the condition [math]\displaystyle{ E\left[ \widehat{\theta } \right] }[/math] [math]\displaystyle{ =\theta }[/math] for all [math]\displaystyle{ \theta \in \Omega . }[/math]
Note that [math]\displaystyle{ E\left[ X \right] }[/math] denotes the expected value of X and is defined (for continuous distributions) by:
- [math]\displaystyle{ \begin{align} E\left[ X \right]= \int_{\varpi }x\cdot f(x)dx \\ X\in & \varpi . \end{align} }[/math]
It can be shown [7][5] that the MLE estimator for the mean of the normal (and lognormal) distribution does satisfy the unbiasedness criteria, or [math]\displaystyle{ E\left[ \widehat{\mu } \right] }[/math] [math]\displaystyle{ =\mu . }[/math] The same is not true for the estimate of the variance [math]\displaystyle{ \hat{\sigma }^{2} }[/math] . The maximum likelihood estimate for the variance for the normal distribution is given by:
- [math]\displaystyle{ \hat{\sigma }^{2}=\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}} }[/math]
with a standard deviation of:
- [math]\displaystyle{ {{\hat{\sigma }}}=\sqrt{\frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}}} }[/math]
These estimates, however, have been shown to be biased. It can be shown [7][5] that the unbiased estimate of the variance and standard deviation for complete data is given by:
- [math]\displaystyle{ \begin{align} \hat{\sigma }^{2}= & \left[ \frac{N}{N-1} \right]\cdot \left[ \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}} \right]=\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}} \\ {{{\hat{\sigma }}}}= & \sqrt{\left[ \frac{N}{N-1} \right]\cdot \left[ \frac{1}{N}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}} \right]} \\ = & \sqrt{\frac{1}{N-1}\underset{i=1}{\overset{N}{\mathop \sum }}\,{{({{t}_{i}}-\bar{T})}^{2}}} \end{align} }[/math]
Note that for larger values of [math]\displaystyle{ N }[/math] , [math]\displaystyle{ \sqrt{\left[ N/(N-1) \right]} }[/math] tends to 1.
Weibull++ by default returns the unbiased standard deviation given above.
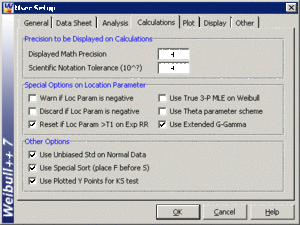
The Use Unbiased Std on Normal Data option in the User Setup under the Calculations tab allows biasing to be considered when estimating the parameters.
When this option is selected, Weibull++ returns the unbiased standard deviation as defined. This is only true for complete data sets. For all other data types, Weibull++ by default returns the standard deviation as defined by Eqn. (normbias2) regardless of the selection status of this option. The next figure shows this setting in Weibull++.
[math]\displaystyle{ }[/math]