Template:Example: Normal Distribution Probability Plot

Normal Distribution Probability Plotting Example

Seven units are put on a life test and run until failure. The failure times are 85, 90, 95, 100, 105, 110, and 115 hours. Assuming a normal distribution, estimate the parameters using probability plotting.

Solution

In order to plot the points for the probability plot, the appropriate unreliability estimate values must be obtained. These will be estimated through the use of median ranks, which can be obtained from statistical tables or the Quick Statistical Reference in Weibull++. The following table shows the times-to-failure and the appropriate median rank values for this example:

[math]\displaystyle{ \begin{matrix} \text{Time-to-} & \text{Median} \\ \text{Failure (hr)} & \text{Rank ( }\!\!%\!\!\text{ )} \\ \text{85} & \text{ 9}\text{.43 }\!\!%\!\!\text{ } \\ \text{90} & \text{22}\text{.85 }\!\!%\!\!\text{ } \\ \text{95} & \text{36}\text{.41 }\!\!%\!\!\text{ } \\ \text{100} & \text{50}\text{.00 }\!\!%\!\!\text{ } \\ \text{105} & \text{63}\text{.59 }\!\!%\!\!\text{ } \\ \text{110} & \text{77}\text{.15 }\!\!%\!\!\text{ } \\ \text{115} & \text{90}\text{.57 }\!\!%\!\!\text{ } \\ \end{matrix} }[/math]

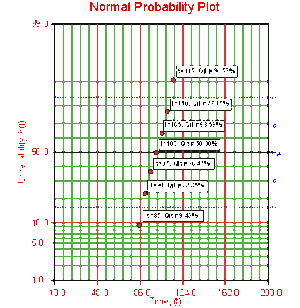
These points can now be plotted on normal probability plotting paper as shown in the next figure.

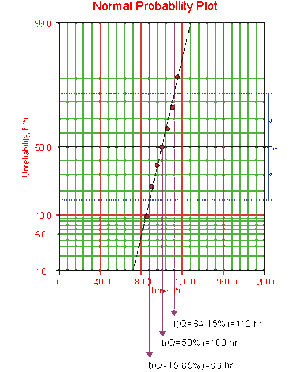
Draw the best possible line through the plot points. The time values where this line intersects the 15.85%, 50%, and 84.15% unreliability values should be projected down to the abscissa, as shown in the following plot.

The estimate of [math]\displaystyle{ \mu }[/math] is determined from the time value at the 50% unreliability level, which in this case is 100 hours. The value of the estimator of [math]\displaystyle{ \sigma }[/math] is determined by Eqn. (sigplot):

[math]\displaystyle{ \begin{align} \widehat{\sigma }= & \frac{t(Q=84.15%)-t(Q=15.85%)}{2} \\ \widehat{\sigma }= & \frac{112-88}{2}=\frac{24}{2} \\ \widehat{\sigma }= & 12\text{ hours} \end{align} }[/math]

Alternately, [math]\displaystyle{ \widehat{\sigma } }[/math] could be determined by measuring the distance from [math]\displaystyle{ t(Q=15.85%) }[/math] to [math]\displaystyle{ t(Q=50%) }[/math] , or [math]\displaystyle{ t(Q=50%) }[/math] to [math]\displaystyle{ t(Q=84.15%) }[/math] , as either of these two distances is equal to the value of one standard deviation.