Template:Rank Regression or Least Squares Parameter Estimation: Difference between revisions

From ReliaWiki
Jump to navigation Jump to search
No edit summary
Line 61: Line 61:




==Analysis of Right Censored (Suspended) Data==
====Background====
All available data should be considered in the analysis of times-to-failure data. This includes the case when a particular unit in a sample has been removed from the test prior to failure. An item, or unit, which is removed from a reliability test prior to failure, or a unit which is in the field and is still operating at the time the reliability of these units is to be determined, is called a ''suspended item or ''right censored observation'' or '' right censored data point''. Suspended items analysis would also be considered when:
#We need to make an analysis of the available results before test completion.
#The failure modes which are occurring are different than those anticipated and such units are withdrawn from the test.
#We need to analyze a single mode and the actual data set is comprised of multiple modes.
#A ''warranty analysis'' is to be made of all units in the field (non-failed and failed units). The non-failed units are considered to be suspended items (or right censored).
====Probability Plotting and Rank Regression Analysis of Right Censored Data====
When using the probability plotting or rank regression method to accommodate the fact that units in the data set did not fail, or were suspended, we need to adjust their probability of failure, or unreliability. As discussed in Chapter 3, estimates of the unreliability for complete data are obtained using the median ranks approach. The following methodology illustrates how adjusted median ranks are computed to account for right censored data.
To better illustrate the methodology, consider the following example [20] where five items are tested resulting in three failures and two suspensions.
{|style= align="center" border="1"
!Item Number(Position)
!State*"F" or "S"
!Life of item, hr
|-align="center"
|1||<math>F_1</math>||5,100
|-align="center"
|2||<math>S_1</math>||9,500
|-align="center"
|3||<math>F_2</math>||15,000
|-align="center"
|4||<math>S_2</math>||22,000
|-align="center"
|5||<math>F_3</math>||40,000
|}
The methodology for plotting suspended items involves adjusting the rank positions and plotting the data based on new positions, determined by the location of the suspensions. If we consider these five units, the following methodology would be used:
The first item must be the first failure; hence, it is assigned failure order number <math>j=1</math>.
The actual failure order number (or position) of the second failure, <math>{{F}_{2}},</math> is in doubt. It could be either in position 2 or in position 3. Had <math>{{S}_{1}}</math> not been withdrawn from the test at 9,500 hours it could have operated successfully past 15,000 hours, thus placing <math>{{F}_{2}}</math> in position 2. Alternatively <math>{{S}_{1}}</math> could also have failed before 15,000 hours, thus placing <math>{{F}_{2}}</math> in position 3. In this case, the failure order number for <math>{{F}_{2}}</math> will be some number between 2 and 3. To determine this number, consider the following:
We can find the number of ways the second failure can occur in either order number 2 (position 2) or order number 3 (position 3). The possible ways are listed next.
{|style= align="center" border="1"
|-
|colspan="6" style="text-align:center;"|<math>F_2</math> in Position 2||rowspan="7" style="text=align:center;"|OR||colspan="2" style="text-align:center;"|<math>F_2</math> in Position 3
|-align="center"
|1||2||3||4||5||6 ||1||2
|-align="center"
|<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||  <math>F_1</math> ||<math>F_1</math>
|-align="center"
|<math>F_2</math>||<math>F_2</math>||<math>F_2</math>||<math>F_2</math>||<math>F_2</math>||<math>F_2</math>  ||<math>S_1</math>||<math>S_1</math>
|-align="center"
|<math>S_1</math>||<math>S_2</math>||<math>F_3</math>||<math>S_1</math>||<math>S_2</math>||<math>F_3</math> ||<math>F_2</math>||<math>F_2</math>
|-align="center"
|<math>S_2</math>||<math>S_1</math>||<math>S_1</math>||<math>F_3</math>||<math>F_3</math>||<math>S_2</math> ||<math>S_2</math>||<math>F_3</math>
|-align="center"
|<math>F_3</math>||<math>F_3</math>||<math>S_2</math>||<math>S_2</math>||<math>S_1</math>||<math>S_1</math> ||<math>F_3</math>||<math>S_2</math>
|}
It can be seen that <math>{{F}_{2}}</math> can occur in the second position six ways and in the third position two ways. The most probable position is the average of these possible ways, or the ''mean order number'' ( <math>MON</math> ), given by:
::<math>{{F}_{2}}=MO{{N}_{2}}=\frac{(6\times 2)+(2\times 3)}{6+2}=2.25</math>
Using the same logic on the third failure, it can be located in position numbers 3, 4 and 5 in the possible ways listed next.
{|style= align="center" border="1"
|-
|colspan="2" style="text-align:center;"|<math>F_3 \text{in Position 3}</math>|| rowspan="7" style="text-align:center;"|OR || colspan="3" style="text-align:center;"|<math>F_3 \text{in Position 4}</math> ||rowspan="7" style="text-align:center;"|OR||colspan="3" style="text-align:center;"|<math>F_3 \text{in Position 5}</math>
|-
|1||2||1||2||3||1||2||3
|-
|<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||<math>F_1</math>||<math>F_1</math>
|-
|<math>F_2</math>||<math>F_2</math>||<math>S_1</math>||<math>F_2</math>||<math>F_2</math>||<math>S_1</math>||<math>F_2</math>||<math>F_2</math>
|-
|<math>F_3</math>||<math>F_3</math>||<math>F_2</math>||<math>S_1</math>||<math>S_2</math>||<math>F_2</math>||<math>S_1</math>||<math>S_2</math>
|-
|<math>S_1</math>||<math>S_2</math>||<math>F_3</math>||<math>F_3</math>||<math>F_3</math>||<math>S_2</math>||<math>S_2</math>||<math>S_1</math>
|-
|<math>S_2</math>||<math>S_1</math>||<math>S_2</math>||<math>S_2</math>||<math>S_1</math>||<math>F_3</math>||<math>F_3</math>||<math>F_3</math>
|}
Then, the mean order number for the third failure,  (Item 5) is:
::<math>MO{{N}_{3}}=\frac{(2\times 3)+(3\times 4)+(3\times 5)}{2+3+3}=4.125</math>
Once the mean order number for each failure has been established, we obtain the median rank positions for these failures at their mean order number. Specifically, we obtain the median rank of the order numbers 1, 2.25 and 4.125 out of a sample size of 5, as given next.
{|style= align="center" border="1"
|-
|colspan="3" style="text-align:center;"|Plotting Positions for the Failures(Sample Size=5)
|-align="center"
!Failure Number
!MON
!Median Rank Position(%)
|-align="center"
|1:<math>F_1</math>||1||13%
|-align="center"
|2:<math>F_2</math>||2.25||36%
|-align="center"
|3:<math>F_3</math>||4.125||71%
|}
Once the median rank values have been obtained, the probability plotting analysis is identical to that presented before. As you might have noticed, this methodology is rather laborious. Other techniques and shortcuts have been developed over the years to streamline this procedure.  For more details on this method, see Kececioglu [20].
====Shortfalls of this Rank Adjustment Method====
Even though the rank adjustment method is the most widely used method for performing suspended items analysis, we would like to point out the following shortcoming.
As you may have noticed from this analysis of suspended items, only the position where the failure occurred is taken into account, and not the exact time-to-suspension. For example, this methodology would yield the exact same results for the next two cases.
{|style= align="center" border="2"
|-
|colspan="3" style="text-align:center;"|Case 1 ||colspan="3" style="text-align:center;"|Case 2
|-align="center"
!Item Number
!State*"F" or "S"
!Life of an item, hr
!Item number
!State*,"F" or "S"
!Life of item, hr
|-align="center"
|1|| <math>F_1</math> ||1,000||1||<math>F_1</math>||1,000
|-align="center"
|2||<math>S_1</math>||1,100||2||<math>S_1</math>||9,700
|-align="center"
|3|| <math>S_2</math>||1,200||3||<math>S_2</math>||9,800
|-align="center"
|4|| <math>S_3</math>||1,300||4||<math>S_3</math>||9,900
|-align="center"
|5|| <math>F_2</math>||10,000||5||<math>F_2</math>||10,000
|-align="center"
|colspan="3" style="text-align:center;"|<math>*F-Failed, S-Suspended</math>||colspan="3" style="text-align:center;"|<math>*F-Failed, S-Suspended</math>
|}
This shortfall is significant when the number of failures is small and the number of suspensions is large and not spread uniformly between failures, as with these data. In cases like this, it is highly recommended that one use maximum likelihood estimation (MLE) to estimate the parameters instead of using least squares, since maximum likelihood does not look at ranks or plotting positions, but rather considers each unique time-to-failure or suspension.
For the data given above the results are as follows:
The estimated parameters using the method just described are the same for both cases (1 and 2):
::<math>\begin{array}{*{35}{l}}
  \widehat{\beta }= & \text{0}\text{.81}  \\
  \widehat{\eta }= & \text{11,417 hr}  \\
\end{array}
</math>
However, the MLE results for Case 1 are:
::<math>\begin{array}{*{35}{l}}
  \widehat{\beta }= & \text{1}\text{.33}  \\
  \widehat{\eta }= & \text{6,900 hr}  \\
\end{array}</math>
and the MLE results for Case 2 are:
As we can see, there is a sizable difference in the results of the two sets calculated using MLE and the results using regression. The results for both cases are identical when using the regression estimation technique, as regression considers only the positions of the suspensions. The MLE results are quite different for the two cases, with the second case having a much larger value of <math>\eta </math>, which is due to the higher values of the suspension times in Case 2. This is because the maximum likelihood technique, unlike rank regression, considers the values of the suspensions when estimating the parameters. This is illustrated in the following section.
====MLE Analysis of Right Censored Data====
When performing maximum likelihood analysis on data with suspended items, the likelihood function needs to be expanded to take into account the suspended items. The overall estimation technique does not change, but another term is added to the likelihood function to account for the suspended items. Beyond that, the method of solving for the parameter estimates remains the same. For example, consider a distribution where <math>x</math> is a continuous random variable with <math>pdf</math> and <math>cdf</math>:
::<math>\begin{align}
    & f(x;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) \\
    & F(x;{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) 
\end{align}
</math>
where <math>{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}</math> are the  unknown parameters which need to be estimated from  <math>R</math>  observed failures at <math>{{T}_{1}},{{T}_{2}}...{{T}_{R}},</math> and <math>M</math> observed suspensions at <math>{{S}_{1}},{{S}_{2}}</math> ... <math>{{S}_{M}},</math> then the likelihood function is formulated as follows:
::<math>\begin{align}
  L({{\theta }_{1}},...,{{\theta }_{k}}|{{T}_{1}},...,{{T}_{R,}}{{S}_{1}},...,{{S}_{M}})= & \underset{i=1}{\overset{R}{\mathop \prod }}\,f({{T}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) \\
  & \cdot \underset{j=1}{\overset{M}{\mathop \prod }}\,[1-F({{S}_{j}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})] 
\end{align}</math>
The parameters are solved by maximizing this equation, as described in Chapter 3.
In most cases, no closed-form solution exists for this maximum or for the parameters. Solutions specific to each distribution utilizing MLE are presented in Appendix C.
====MLE Analysis of Interval and Left Censored Data====
The inclusion of left and interval censored data in an MLE solution for parameter estimates involves adding a term to the likelihood equation to account for the data types in question. When using interval data, it is assumed that the failures occurred in an interval, '' i.e.'' in the interval from time <math>A</math> to time <math>B</math> (or from time <math>0</math> to time <math>B</math> if left censored), where <math>A<B</math>.
In the case of interval data, and given <math>P</math> interval observations, the likelihood function is modified by multiplying the likelihood function with an additional term as follows:
::<math>\begin{align}
  L({{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}|{{x}_{1}},{{x}_{2}},...,{{x}_{P}})= & \underset{i=1}{\overset{P}{\mathop \prod }}\,\{F({{x}_{i}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}}) \\
  & \ \ -F({{x}_{i-1}};{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{k}})\} 
\end{align}
</math>
Note that if only interval data are present, this term will represent the entire likelihood function for the MLE solution. The next section gives a formulation of the complete likelihood function for all possible censoring schemes.
====ReliaSoft's Alternate Rank Method (RRM)====
Difficulties arise when attempting the probability plotting or rank regression analysis of interval or left censored data, especially when an overlap on the intervals is present. This difficulty arises when attempting to estimate the exact time within the interval when the failure actually occurs. The ''standard regression method'' (SRM) is not applicable when dealing with interval data; thus ReliaSoft has formulated a more sophisticated methodology to allow for more accurate probability plotting and regression analysis of data sets with interval or left censored data. This method utilizes the traditional rank regression method and iteratively improves upon the computed ranks by parametrically recomputing new ranks and the most probable failure time for interval data. See Appendix B for a step-by-step example of this method.
====The Complete Likelihood Function====
We have now seen that obtaining MLE parameter estimates for different types of data involves incorporating different terms in the likelihood function to account for complete data, right censored data, and left, interval censored data. After including the terms for the different types of data, the likelihood function can now be expressed in its complete form or,
::<math>\begin{array}{*{35}{l}}
    L= & \underset{i=1}{\mathop{\overset{R}{\mathop{\prod }}\,}}\,f({{T}_{i}};{{\theta }_{1}},...,{{\theta }_{k}})\cdot \underset{j=1}{\mathop{\overset{M}{\mathop{\prod }}\,}}\,[1-F({{S}_{j}};{{\theta }_{1}},...,{{\theta }_{k}})]  \\
    & \cdot \underset{l=1}{\mathop{\overset{P}{\mathop{\prod }}\,}}\,\left\{ F({{I}_{{{l}_{U}}}};{{\theta }_{1}},...,{{\theta }_{k}})-F({{I}_{{{l}_{L}}}};{{\theta }_{1}},...,{{\theta }_{k}}) \right\}  \\
\end{array}
</math>
:where
::<math> L\to L({{\theta }_{1}},...,{{\theta }_{k}}|{{T}_{1}},...,{{T}_{R}},{{S}_{1}},...,{{S}_{M}},{{I}_{1}},...{{I}_{P}}),</math>
:and
:# <math>R</math>  is the number of units with exact failures
:# <math>M</math>  is the number of suspended units
:# <math>P</math>  is the number of units with left censored or interval times-to-failure
:# <math>{{\theta }_{k}}</math>  are the parameters of the distribution
:# <math>{{T}_{i}}</math>  is the <math>{{i}^{th}}</math> time to failure
:# <math>{{S}_{j}}</math>  is the <math>{{j}^{th}}</math> time of suspension
:# <math>{{I}_{{{l}_{U}}}}</math>  is the ending of the time interval of the <math>{{l}^{th}}</math> group
:# <math>{{I}_{{{l}_{L}}}}</math>  is the beginning of the time interval of the <math>{l^{th}}</math> group
The total number of units is <math>N=R+M+P</math>. It should be noted that in this formulation if either <math>R</math>, <math>M</math> or <math>P</math> is zero the product term associated with them is assumed to be one and not zero.




Revision as of 18:30, 29 October 2011

Rank Regression or Least Squares Parameter Estimation

Using the idea of probability plotting, regression analysis mathematically fits the best straight line to a set of points, in an attempt to estimate the parameters. Essentially, this is a mathematically based version of the probability plotting method discussed previously.

Background Theory

The method of linear least squares is used for all regression analysis performed by Weibull++, except for the cases of the three-parameter Weibull, mixed Weibull, gamma and generalized gamma distributions where a non-linear regression technique is employed. The terms linear regression and least squares are used synonymously in this reference. The term rank regression is used instead of least squares, or linear regression, because the regression is performed on the rank values, more specifically, the median rank values (represented on the y-axis). 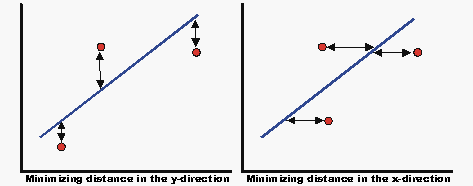The method of least squares requires that a straight line be fitted to a set of data points, such that the sum of the squares of the distance of the points to the fitted line is minimized. This minimization can be performed in either the vertical or horizontal direction. If the regression is on [math]\displaystyle{ X }[/math], then the line is fitted so that the horizontal deviations from the points to the line are minimized. If the regression is on Y, then this means that the distance of the vertical deviations from the points to the line is minimized. This is illustrated in the following figure.


Ldachp3fig2.gif

Rank Regression on [math]\displaystyle{ Y }[/math]

Assume that a set of data pairs [math]\displaystyle{ ({x_1},{y_1}) }[/math], [math]\displaystyle{ ({{x}_{2}},{{y}_{2}}) }[/math],..., [math]\displaystyle{ ({{x}_{N}},{{y}_{N}}) }[/math] were obtained and plotted, and that the [math]\displaystyle{ x }[/math] -values are known exactly. Then, according to the least squares principle, which minimizes the vertical distance between the data points and the straight line fitted to the data, the best fitting straight line to these data is the straight line [math]\displaystyle{ y=\hat{a}+\hat{b}x }[/math] (where the recently introduced [math]\displaystyle{ (\hat{ }) }[/math] symbol indicates that this value is an estimate) such that: .. and where [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat b }[/math] are the least squares estimates of [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math],and [math]\displaystyle{ N }[/math] is the number of data points. These equations are minimized by estimates of [math]\displaystyle{ \widehat a }[/math] and [math]\displaystyle{ \widehat{b} }[/math] such that:

[math]\displaystyle{ \hat{a}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}}{N}=\bar{y}-\hat{b}\bar{x} }[/math]
and:
[math]\displaystyle{ \hat{b}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,x_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}} \right)}^{2}}}{N}} }[/math]

Rank Regression on X

Assume that a set of data pairs .., [math]\displaystyle{ ({x_2},{y_2}) }[/math],..., [math]\displaystyle{ ({x_N},{y_N}) }[/math]were obtained and plotted, and that the y-values are known exactly. The same least squares principle is applied, this time minimizing the horizontal distance between the data points and the straight line fitted to the data. The best fitting straight line to these data is the straight line [math]\displaystyle{ x=\widehat{a}+\widehat{b}y }[/math] such that:

[math]\displaystyle{ \underset{i=1}{\overset{N}{\mathop \sum }}\,{{(\widehat{a}+\widehat{b}{{y}_{i}}-{{x}_{i}})}^{2}}=min(a,b)\underset{i=1}{\overset{N}{\mathop \sum }}\,{{(a+b{{y}_{i}}-{{x}_{i}})}^{2}} }[/math]

Again, [math]\displaystyle{ \widehat{a} }[/math] and [math]\displaystyle{ \widehat b }[/math] are the least squares estimates of and [math]\displaystyle{ b, }[/math] and [math]\displaystyle{ N }[/math] is the number of data points. These equations are minimized by estimates of [math]\displaystyle{ \widehat a }[/math] and [math]\displaystyle{ \widehat{b} }[/math] such that:

[math]\displaystyle{ \hat{a}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}}{N}-\hat{b}\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}=\bar{x}-\hat{b}\bar{y} }[/math]
and:
[math]\displaystyle{ \widehat{b}=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}}{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,y_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}} \right)}^{2}}}{N}} }[/math]

The corresponding relations for determining the parameters for specific distributions (i.e., Weibull, exponential, etc.), are presented in the chapters covering that distribution.

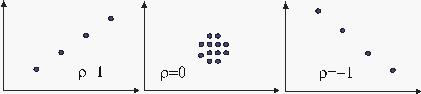
The Correlation Coefficient

The correlation coefficient is a measure of how well the linear regression model fits the data and is usually denoted by [math]\displaystyle{ \rho }[/math]. In the case of life data analysis, it is a measure for the strength of the linear relation (correlation) between the median ranks and the data. The population correlation coefficient is defined as follows:

[math]\displaystyle{ \rho =\frac{{{\sigma }_{xy}}}{{{\sigma }_{x}}{{\sigma }_{y}}} }[/math]

where [math]\displaystyle{ {{\sigma }_{xy}}= }[/math] covariance of and [math]\displaystyle{ y }[/math] , [math]\displaystyle{ {{\sigma }_{x}}= }[/math] standard deviation of [math]\displaystyle{ x }[/math] , and [math]\displaystyle{ {\sigma _y} = }[/math] standard deviation of [math]\displaystyle{ y }[/math].

The estimator of [math]\displaystyle{ \rho }[/math] is the sample correlation coefficient, [math]\displaystyle{ \hat{\rho } }[/math], given by,

[math]\displaystyle{ \hat{\rho }=\frac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}{{y}_{i}}-\tfrac{\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}}\underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}}}{N}}{\sqrt{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,x_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{x}_{i}} \right)}^{2}}}{N} \right)\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,y_{i}^{2}-\tfrac{{{\left( \underset{i=1}{\overset{N}{\mathop{\sum }}}\,{{y}_{i}} \right)}^{2}}}{N} \right)}} }[/math]

The range of [math]\displaystyle{ \hat \rho }[/math] is [math]\displaystyle{ -1\le \hat{\rho }\le 1. }[/math]

Ldachp3fig3.gif

The closer the value is to [math]\displaystyle{ \pm 1 }[/math], the better the linear fit. Note that +1 indicates a perfect fit (the paired values ( [math]\displaystyle{ {{x}_{i}},{{y}_{i}} }[/math] ) lie on a straight line) with a positive slope, while -1 indicates a perfect fit with a negative slope. A correlation coefficient value of zero would indicate that the data are randomly scattered and have no pattern or correlation in relation to the regression line model.

Comments on the Least Squares Method

The least squares estimation method is quite good for functions that can be linearized. For these distributions, the calculations are relatively easy and straightforward, having closed-form solutions which can readily yield an answer without having to resort to numerical techniques or tables. Further, this technique provides a good measure of the goodness-of-fit of the chosen distribution in the correlation coefficient. Least squares is generally best used with data sets containing complete data, that is, data consisting only of single times-to-failure with no censored or interval data. Chapter 4 details the different data types, including complete, left censored, right censored (or suspended) and interval data.







See also

Retrieved from "https://www.reliawiki.com/index.php?title=Template:Rank_Regression_or_Least_Squares_Parameter_Estimation&oldid=10670"