Time-Varying Stress Models

Time-Varying Stress Models

Introduction

Traditionally, accelerated tests that use a time-varying stress application have been used to assure failures quickly. This is highly desirable given the pressure on industry today to shorten new product introduction time. The most basic type of time-varying stress test is a step-stress test. In step-stress accelerated testing, the test units are subjected to successively higher stress levels in predetermined stages, and thus follow a time-varying stress profile. The units usually start at a lower stress level and at a predetermined time, or failure number, the stress is increased and the test continues. The test is terminated when all units have failed, when a certain number of failures are observed or when a certain time has elapsed. Step-stress testing can substantially shorten the reliability test's duration. In addition to step-stress testing, there are many other types of time-varying stress profiles that can be used in accelerated life testing. However, it should be noted that there is more uncertainty in the results from such time-varying stress tests than from traditional constant stress tests of the same length and sample size.
When dealing with data from accelerated tests with time-varying stresses, the life-stress relationship must take into account the cumulative effect of the applied stresses. Such a model is commonly referred to as a cumulative damage or cumulative exposure model. Nelson [28] defines and presents the derivation and assumptions of such a model. ALTA PRO includes the cumulative damage model for the analysis of time-varying stress data. This chapter presents an introduction to the model formulation and its application.

Model Formulation

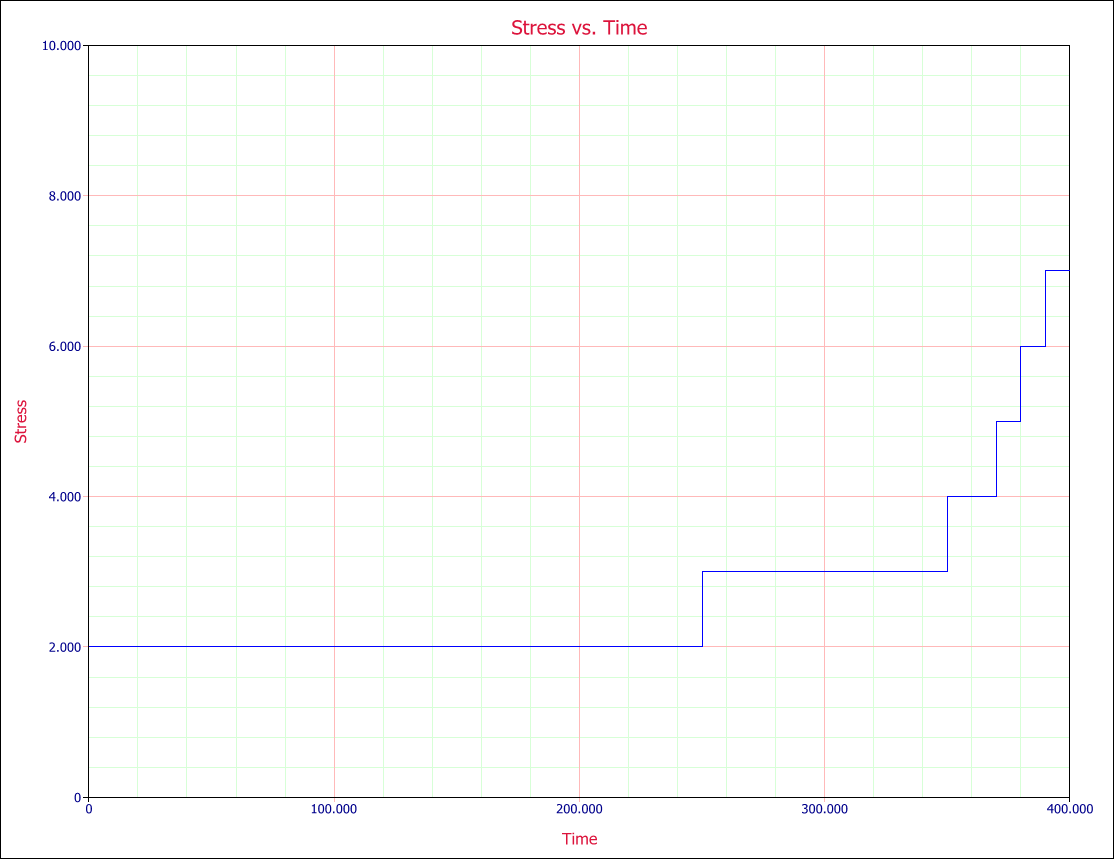
To formulate the cumulative exposure/damage model, consider a simple step-stress experiment where an electronic component was subjected to a voltage stress, starting at 2V (use stress level) and increased to 7V in stepwise increments, as shown in Figure 1. The following steps, in hours, were used to apply stress to the products under test: 0 to 250, 2V; 250 to 350, 3V; 350 to 370, 4V; 370 to 380, 5V; 380 to 390, 6V; and 390 to 400, 7V.

Fig. 1: Step profile for a simple voltage stress test.

In this example, eleven units were available for the test. All eleven units were tested using this same stress profile. Units that failed were removed from the test and their total times on test were recorded. The following times-to-failure were observed in the test, in hours: 280, 310, 330, 352, 360, 366, 371, 374, 378, 381 and 385. The first failure in this test occurred at 280 hours when the stress was 3V. During the test, this unit experienced a period of time at 2V before failing at 3V. If the stress were 2V, one would expect the unit to fail at a time later than 280 hours, while if the unit were always at 3V, one would expect that failure time to be sooner than 280 hrs. The problem faced by the analyst in this case is to determine some equivalency between the stresses. In other words, what is the equivalent of 280 hours (with 250 hours spent at 2V and 30 hours spent at 3V) at a constant 2V stress or at a constant 3V stress?

Mathematical Formulation for a Step-Stress Model

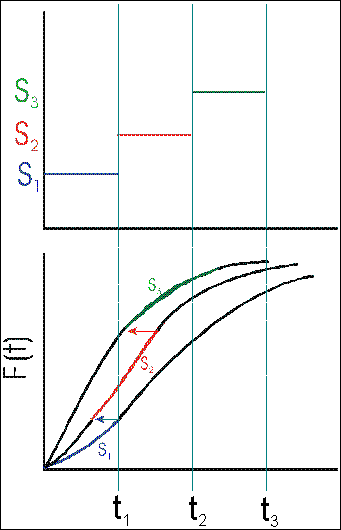
To mathematically formulate the model, consider the step-stress test shown in Fig. 2, with stresses S1, S2 and S3. Furthermore, assume that the underlying life distribution is the Weibull distribution, and also assume an inverse power law relationship between the Weibull scale parameter and the applied stress.

Fig. 2: Step-stress profile and the correstponding life distributions.

From the inverse power law relationship, the scale parameter, [math]\displaystyle{ \eta }[/math] , of the Weibull distribution can be expressed as an inverse power function of the stress, [math]\displaystyle{ V }[/math] or:

[math]\displaystyle{ \eta(V)=\frac{1}{{{K}{V}}^\eta } }[/math]

where [math]\displaystyle{ K }[/math] and [math]\displaystyle{ n }[/math] are model parameters. The fraction of the units failing by time [math]\displaystyle{ {{t}_{1}} }[/math] under a constant stress , is given by:

[math]\displaystyle{ F(t;V)=1-R(t;V) }[/math]

where:

[math]\displaystyle{ R(t;V)={{e}^{-{{\left[ \tfrac{t}{\eta (V)} \right]}^{\beta }}}} }[/math]

Combining Eqns. (ipl), (cdf) and (rel) yields the [math]\displaystyle{ cdf }[/math] for each constant stress level or:

[math]\displaystyle{ \begin{align} & {{F}_{1}}(t;{{S}_{1}})= & 1-{{e}^{-{{(KS_{1}^{n}t)}^{\beta }}}} \\ & {{F}_{2}}(t;{{S}_{2}})= & 1-{{e}^{-{{(KS_{2}^{n}t)}^{\beta }}}} \\ & {{F}_{3}}(t;{{S}_{3}})= & 1-{{e}^{-{{(KS_{3}^{n}t)}^{\beta }}}} \end{align} }[/math]

The above equations would suffice if the units did not experience different stresses during the test, as they did in this case. To analyze the data from this step-stress test, a cumulative exposure model is needed. Such a model will relate the life distribution, in this case the Weibull distribution, of the units at one stress level to the distribution at the next stress level. In formulating this model, it is assumed that the remaining life of the test units depends only on the cumulative exposure the units have seen and that the units do not remember how such exposure was accumulated. Moreover, since the units are held at a constant stress at each step, the surviving units will fail according to the distribution at the current step, but with a starting age corresponding to the total accumulated time up to the beginning of the current step. This model can be formulated as follows:
• Units failing during the first step have not experienced any other stresses and will fail according to Eqn. (cdfst1). Units that made it to the second step will fail according to Eqn. (cdfst2), but will have accumulated some equivalent age, [math]\displaystyle{ {{\varepsilon }_{1}}, }[/math] at this stress level (given the fact that they have spent [math]\displaystyle{ {{t}_{1}} }[/math] hours at [math]\displaystyle{ {{S}_{1}}) }[/math] or: •
• [math]\displaystyle{ {{F}_{2}}(t;{{S}_{2}})=1-{{e}^{-{{[KS_{2}^{n}((t-{{t}_{1}})+{{\varepsilon }_{1}})]}^{\beta }}}} }[/math] •
• In other words, the probability that the units will fail at a time, [math]\displaystyle{ t }[/math] , while at [math]\displaystyle{ {{S}_{2}} }[/math] and between [math]\displaystyle{ {{t}_{1}} }[/math]
and
.. is equivalent to the probability that the units would fail after accumulating [math]\displaystyle{ (t-{{t}_{1}}) }[/math] plus some equivalent time, [math]\displaystyle{ {{\varepsilon }_{1}}, }[/math] to account for the exposure the units have seen at [math]\displaystyle{ {{S}_{1}} }[/math] .
• The equivalent time, [math]\displaystyle{ {{\varepsilon }_{1}}, }[/math] will be the time by which the probability of failure at [math]\displaystyle{ {{S}_{2}} }[/math] is equal to the probability of failure at [math]\displaystyle{ {{S}_{1}} }[/math]
after an exposure of
[math]\displaystyle{ {{t}_{1}} }[/math] or:

• [math]\displaystyle{ \begin{align} & {{F}_{1}}({{t}_{1}};{{S}_{1}})= & {{F}_{2}}({{\varepsilon }_{1}},{{S}_{2}}) \\ & 1-{{e}^{-{{(KS_{1}^{n}{{t}_{1}})}^{\beta }}}}= & 1-{{e}^{-{{(KS_{2}^{n}{{\varepsilon }_{1}})}^{\beta }}}} \\ & S_{1}^{n}{{t}_{1}}= & S_{2}^{n}{{\varepsilon }_{1}} \\ & {{\varepsilon }_{1}}= & {{t}_{1}}{{\left( \frac{{{S}_{1}}}{{{S}_{2}}} \right)}^{n}} \end{align} }[/math]

• One would repeat this for step 3 taking into account the accumulated exposure during steps 1 and 2, or in more general terms and for the [math]\displaystyle{ {{i}^{th}} }[/math] step:

• [math]\displaystyle{ {{F}_{i}}(t;{{S}_{i}})=1-{{e}^{-{{[KS_{i}^{n}((t-{{t}_{i-1}})+{{\varepsilon }_{i-1}})]}^{\beta }}}} }[/math]

• where:

• [math]\displaystyle{ {{\varepsilon }_{i-1}}=({{t}_{i-1}}-{{t}_{i-2}}){{\left( \frac{{{S}_{i-1}}}{{{S}_{i}}} \right)}^{n}}+{{\varepsilon }_{i-2}} }[/math]

• Once the [math]\displaystyle{ cdf }[/math] for each step has been obtained, the [math]\displaystyle{ pdf }[/math] can also then be determined utilizing:

[math]\displaystyle{ {{f}_{i}}(t,{{S}_{i}})=-\frac{d}{dt}\left[ {{F}_{i}}(t,{{S}_{i}}) \right] }[/math]

Once the model has been formulated, model parameters (i.e. [math]\displaystyle{ K }[/math] , [math]\displaystyle{ n }[/math] and [math]\displaystyle{ \beta }[/math] ) can be computed utilizing maximum likelihood estimation methods. The previous example can be expanded for any time-varying stress. ALTA PRO allows you to define any stress profile. For example, the stress can be a ramp stress, a monotonically increasing stress, sinusoidal, etc. This section presents a generalized formulation of the cumulative damage model, where stress can be any function of time. Cumulative Damage Power Relationship This section presents a generalized formulation of the cumulative damage model where stress can be any function of time and the life-stress relationship is based on the power relationship. Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the power law relationship, the life-stress relationship is given by:

[math]\displaystyle{ L(x(t))={{\left( \frac{a}{x(t)} \right)}^{n}} }[/math]

In ALTA PRO, the above relationship is actually presented in a format consistent with the general log-linear (GLL) relationship for the power law relationship:

[math]\displaystyle{ L(x(t))={{e}^{{{\alpha }_{0}}+{{\alpha }_{1}}\ln \left( x(t) \right)}} }[/math]

Therefore, instead of displaying [math]\displaystyle{ a }[/math] and [math]\displaystyle{ n }[/math] as the calculated parameters, the following reparameterization is used:

[math]\displaystyle{ \begin{align} & {{\alpha }_{0}}= & \ln ({{a}^{n}}) \\ & {{\alpha }_{1}}= & -n \end{align} }[/math]

Cumulative Damage Power - Exponential

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the power law relationship, the mean life is given by:

[math]\displaystyle{ \frac{1}{m(t,x)}=s(t,x)={{\left( \frac{x(t)}{a} \right)}^{n}} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))={{e}^{-I(t,x)}} }[/math]

where:

[math]\displaystyle{ I(t,x)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\left( \frac{x(u)}{a} \right)}^{n}}du }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=s(t,x){{e}^{-I(t,x)}} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and
confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest (e.g. mean life, failure rate, etc.) can be obtained utilizing the statistical properties definitions presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [s({{T}_{i}},{{x}_{i}})]-\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\left( I({{T}_{i}},{{x}_{i}}) \right) \\ & & -\overset{S}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }\left( I(T_{i}^{\prime },x_{i}^{\prime }) \right)+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })}} \\ & R_{Ri}^{\prime \prime }(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })}} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points. • [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group. • [math]\displaystyle{ {{T}_{i}} }[/math] is the ex[math]\displaystyle{ N_{i}^{\prime } }[/math]act failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group. • [math]\displaystyle{ S }[/math] is the number of groups of suspension data points. • is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points. • [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group. • [math]\displaystyle{ FI }[/math] is the number of interval data groups. • [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals. • [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval. • [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage Power - Weibull

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the power law relationship, the characteristic life is given by:

[math]\displaystyle{ \frac{1}{\eta (t,x)}=s(t,x)={{\left( \frac{x(t)}{a} \right)}^{n}} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))={{e}^{-{{\left( I(t,x) \right)}^{\beta }}}} }[/math]

where:

[math]\displaystyle{ I(t,x)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\left( \frac{x(u)}{a} \right)}^{n}}du }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=\beta s(t,x){{\left( I(t,x) \right)}^{\beta -1}}{{e}^{-{{\left( I(t,x) \right)}^{\beta }}}} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [\beta s({{T}_{i}},{{x}_{i}}){{\left( I({{T}_{i}},{{x}_{i}}) \right)}^{\beta -1}}]-\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{\left( I({{T}_{i}},{{x}_{i}}) \right)}^{\beta }} \\ & & -\overset{S}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }{{\left( I(T_{i}^{\prime },x_{i}^{\prime }) \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-{{\left( I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime }) \right)}^{\beta }}}} \\ & R_{Ri}^{\prime \prime }(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-{{\left( I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime }) \right)}^{\beta }}}} \end{align} }[/math]

and:

[math]\displaystyle{ {{F}_{e}} }[/math]

• is the number of groups of exact times-to-failure data points. • [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group. • [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group. • [math]\displaystyle{ S }[/math] is the number of groups of suspension data points. • [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points. • [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group. • [math]\displaystyle{ FI }[/math] is the number of interval data groups. • [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals. • [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval. • [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage Power - Lognormal

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the power law relationship, the median life is given by:

[math]\displaystyle{ \frac{1}{\breve{T}(t,x)}=s(t,x)={{\left( \frac{x(t)}{a} \right)}^{n}} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))=1-\Phi (z) }[/math]

where:

[math]\displaystyle{ z(t,x)=\frac{\ln I(t,x)}{\sigma _{T}^{\prime }} }[/math]

and:

[math]\displaystyle{ I(t,x)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\left( \frac{x(u)}{a} \right)}^{n}}du }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=\frac{s(t,x)\varphi (z(t,x))}{\sigma _{T}^{\prime }I(t,x)} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [\frac{s({{T}_{i}},{{x}_{i}})\varphi (z({{T}_{i}},{{x}_{i}}))}{\sigma _{T}^{\prime }I({{T}_{i}},{{x}_{i}})}] \\ & & \overset{S}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }\ln \left( 1-\Phi (z(T_{i}^{\prime },x_{i}^{\prime })) \right)+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & z_{Ri}^{\prime \prime }= & \frac{\ln I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })}{\sigma _{T}^{\prime }} \\ & z_{Li}^{\prime \prime }= & \frac{\ln I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })}{\sigma _{T}^{\prime }} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact time-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage Arrhenius Relationship

This section presents a generalized formulation of the cumulative damage model where stress can be any function of time and the life-stress relationship is based on the Arrhenius life-stress relationship. Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the Arrhenius relationship, the life-stress relationship is given by:

[math]\displaystyle{ L(x(t))=C{{e}^{\tfrac{b}{x(t)}}} }[/math]

In ALTA PRO, the above relationship is actually presented in a format consistent with the general log-linear (GLL) relationship for the Arrhenius relationship:

[math]\displaystyle{ L(x(t))={{e}^{{{\alpha }_{0}}+{{\alpha }_{1}}\tfrac{1}{x(t)}}} }[/math]

Therefore, instead of displaying and [math]\displaystyle{ b\lt \lt math\gt C }[/math]/math> as the calculated parameters, the following reparameterization is used:

[math]\displaystyle{ \begin{align} & {{\alpha }_{0}}= & \ln (C) \\ & {{\alpha }_{1}}= & b \end{align} }[/math]

Cumulative Damage Arrhenius - Exponential

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the Arrhenius relationship, the mean life is:

[math]\displaystyle{ \frac{1}{m(t,x)}=s(t,x)=\frac{{{e}^{\tfrac{-b}{x(t)}}}}{C} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))={{e}^{-I(t,x)}} }[/math]

where:

[math]\displaystyle{ I(t,x)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,\frac{{{e}^{\tfrac{-b}{x(u)}}}}{C}du }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=s(t,x){{e}^{-I(t,x)}} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [s({{T}_{i}},{{x}_{i}})]-\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\left( I({{T}_{i}},{{x}_{i}}) \right) \\ & & -\overset{S}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }\left( I(T_{i}^{\prime },x_{i}^{\prime }) \right)+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })}} \\ & R_{Ri}^{\prime \prime }(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })}} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact time-to-failure data points. • [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group. • [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group. • [math]\displaystyle{ S }[/math] is the number of groups of suspension data points. • [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points. • [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group. • [math]\displaystyle{ FI }[/math] is the number of interval data groups. • [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals. • [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval. • [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage Arrhenius - Weibull

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the Arrhenius relationship, the characteristic life is given by:

[math]\displaystyle{ \frac{1}{\eta (t,x)}=s(t,x)=\frac{{{e}^{\tfrac{-b}{x(t)}}}}{C} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))={{e}^{-{{\left( I(t,x) \right)}^{\beta }}}} }[/math]

where:

[math]\displaystyle{ I(t,x)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,\frac{{{e}^{\tfrac{-b}{x(u)}}}}{C}du }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=\beta s(t,x){{\left( I(t,x) \right)}^{\beta -1}}{{e}^{-{{\left( I(t,x) \right)}^{\beta }}}} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [\beta s({{T}_{i}},{{x}_{i}}){{\left( I({{T}_{i}},{{x}_{i}}) \right)}^{\beta -1}}]-\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{\left( I({{T}_{i}},{{x}_{i}}) \right)}^{\beta }} \\ & & -\overset{S}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }{{\left( I(T_{i}^{\prime },x_{i}^{\prime }) \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-{{\left( I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime }) \right)}^{\beta }}}} \\ & R_{Ri}^{\prime \prime }(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-{{(I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime }))}^{\beta }}}} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact time-to-failure data points. • [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group. • [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group. • [math]\displaystyle{ S }[/math] is the number of groups of suspension data points. • [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points. • [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group. • [math]\displaystyle{ FI }[/math] is the number of interval data groups. • [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals. • [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval. • [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage Arrhenius - Lognormal

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the Arrhenius relationship, the median life is given by:

[math]\displaystyle{ \frac{1}{\breve{T}(t,x)}=s(t,x)=\frac{{{e}^{\tfrac{-b}{x(t)}}}}{C} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))=1-\Phi (z) }[/math]

where:

[math]\displaystyle{ z(t,x)=\frac{\ln I(t,x)}{\sigma _{T}^{\prime }} }[/math]

and:

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=\frac{s(t,x)\varphi (z(t,x))}{\sigma _{T}^{\prime }I(t,x)} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows,

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [\frac{s({{T}_{i}},{{x}_{i}})\varphi (z({{T}_{i}},{{x}_{i}}))}{\sigma _{T}^{\prime }I({{T}_{i}},{{x}_{i}})}] \\ & & \overset{S}{\mathop{+\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }\ln \left( 1-\Phi (z(T_{i}^{\prime },x_{i}^{\prime })) \right)+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & z_{Ri}^{\prime \prime }= & \frac{\ln I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })}{\sigma _{T}^{\prime }} \\ & z_{Li}^{\prime \prime }= & \frac{\ln I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })}{\sigma _{T}^{\prime }} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• .. is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage Exponential Relationship

This section presents a generalized formulation of the cumulative damage model where stress can be any function of time and the life-stress relationship is based on the exponential relationship. Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the exponential relationship, the life-stress relationship is given by:

[math]\displaystyle{ L(x(t))=C{{e}^{bx(t)}} }[/math]

In ALTA PRO, the above relationship is actually presented in a format consistent with the general log-linear (GLL) relationship for the exponential relationship:

Therefore, instead of dis[math]\displaystyle{ C }[/math]playing and [math]\displaystyle{ b }[/math] as the calculated parameters, the following reparameterization is used:

[math]\displaystyle{ \begin{align} & {{\alpha }_{0}}= & \ln (C) \\ & {{\alpha }_{1}}= & b \end{align} }[/math]

Cumulative Damage Exponential - Exponential

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the exponential life-stress relationship, the mean life is given by:

[math]\displaystyle{ \frac{1}{m(t,x)}=s(t,x)=\frac{{{e}^{-bx(t)}}}{C} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))={{e}^{-I(t,x)}} }[/math]

where:

[math]\displaystyle{ I(t,x)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,\frac{{{e}^{-bx(u)}}}{C}du }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=s(t,x){{e}^{-I(t,x)}} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [s({{T}_{i}},{{x}_{i}})]-\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\left( I({{T}_{i}},{{x}_{i}}) \right) \\ & & -\overset{S}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }\left( I(T_{i}^{\prime },x_{i}^{\prime }) \right)+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })}} \\ & R_{Ri}^{\prime \prime }(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })}} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact time-to-failure data points. • [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group. • [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group. • [math]\displaystyle{ S }[/math] is the number of groups of suspension data points. • [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points. • [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group. • [math]\displaystyle{ FI }[/math] is the number of interval data groups. • [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals. • [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval. • [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage Exponential - Weibull

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the exponential life-stress relationship, the characteristic life is given by:

[math]\displaystyle{ \frac{1}{\eta (t,x)}=s(t,x)=\frac{{{e}^{-b\cdot x(t)}}}{C} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))={{e}^{-{{\left( I(t,x) \right)}^{\beta }}}} }[/math]

where:

[math]\displaystyle{ I(t,x)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,\frac{{{e}^{-bx(u)}}}{C}du }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=\beta s(t,x){{\left( I(t,x) \right)}^{\beta -1}}{{e}^{-{{\left( I(t,x) \right)}^{\beta }}}} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [\beta s({{T}_{i}},{{x}_{i}}){{\left( I({{T}_{i}},{{x}_{i}}) \right)}^{\beta -1}}] \\ & & -\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{\left( I({{T}_{i}},{{x}_{i}}) \right)}^{\beta }}-\overset{S}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }{{\left( I(T_{i}^{\prime },x_{i}^{\prime }) \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-{{\left( I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime }) \right)}^{\beta }}}} \\ & R_{Ri}^{\prime \prime }(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })= & {{e}^{-{{\left( I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime }) \right)}^{\beta }}}} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact time-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage Exponential - Lognormal

Given a time-varying stress [math]\displaystyle{ x(t) }[/math] and assuming the exponential life-stress relationship, the median life is:

[math]\displaystyle{ \frac{1}{\breve{T}(t,x)}=s(t,x)=\frac{{{e}^{-bx(t)}}}{C} }[/math]

The reliability function of the unit under a single stress is given by:

[math]\displaystyle{ R(t,x(t))=1-\Phi (z) }[/math]

where:

[math]\displaystyle{ z(t,x)=\frac{\ln I(t,x)}{\sigma _{T}^{\prime }} }[/math]

and:

[math]\displaystyle{ I(t,x)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,\frac{{{e}^{-bx(u)}}}{C}du }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,x)=\frac{s(t,x)\varphi (z(t,x))}{\sigma _{T}^{\prime }I(t,x)} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [\frac{s({{T}_{i}},{{x}_{i}})\varphi (z({{T}_{i}},{{x}_{i}}))}{\sigma _{T}^{\prime }I({{T}_{i}},{{x}_{i}})}] \\ & & \overset{S}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }\ln \left( 1-\Phi (z(T_{i}^{\prime },x_{i}^{\prime })) \right)+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & z_{Ri}^{\prime \prime }= & \frac{\ln I(T_{Ri}^{\prime \prime },x_{i}^{\prime \prime })}{\sigma _{T}^{\prime }} \\ & z_{Li}^{\prime \prime }= & \frac{\ln I(T_{Li}^{\prime \prime },x_{i}^{\prime \prime })}{\sigma _{T}^{\prime }} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact times-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.[math]\displaystyle{ S }[/math]
• is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Example

Using the simple step-stress data given in Section 12.2, one would define [math]\displaystyle{ x(t) }[/math] as:

[math]\displaystyle{ \begin{align} & x(t)= & 2,\text{ }0\lt t\le 250 \\ & = & 3,\text{ }250\lt t\le 350 \\ & = & 4,\text{ }350\lt t\le 370 \\ & = & 5,\text{ }370\lt t\le 380 \\ & = & 6,\text{ }380\lt t\le 390 \\ & = & 7,\text{ }390\lt t\le +\infty \end{align} }[/math]

Step-stress profile is entered in ALTA as follows.

The times to failure are entered as a data folio in ALTA as follows.

Assuming a power relation as the underlying life-stress relationship and the Weibull distribution as the underlying life distribution, one can then formulate the log-likelihood function for the above data set as,

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{F}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,\ln \left\{ \beta {{\left[ \frac{x(t)}{a} \right]}^{n}}{{\left[ \mathop{}_{0}^{{{t}_{i}}}{{\left[ \frac{\left[ x(u) \right]}{a} \right]}^{n}}du \right]}^{\beta -1}} \right\} \\ & & -\overset{F}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,\left\{ {{\left[ \mathop{}_{0}^{{{t}_{i}}}{{\left[ \frac{\left[ x(u) \right]}{a} \right]}^{n}}du \right]}^{\beta }} \right\} \end{align} }[/math]

where:
• [math]\displaystyle{ F }[/math] is the number of exact time-to-failure data points.
• [math]\displaystyle{ \beta }[/math] is the Weibull shape parameter.
• [math]\displaystyle{ a }[/math] and [math]\displaystyle{ n }[/math] are the IPL parameters.
• [math]\displaystyle{ x(t) }[/math] is the stress profile function.
• [math]\displaystyle{ {{t}_{i}} }[/math] is the [math]\displaystyle{ {{i}^{th}} }[/math] time to failure.
The parameter estimates for [math]\displaystyle{ \hat{\beta } }[/math] , [math]\displaystyle{ \hat{a} }[/math] and [math]\displaystyle{ \hat{n} }[/math] can be obtained by simultaneously solving, [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial a}=0 }[/math] and [math]\displaystyle{ \tfrac{\partial \Lambda }{\partial n}=0 }[/math] . Using ALTA PRO, the parameter estimates for this data set are:

[math]\displaystyle{ \begin{align} & \widehat{\beta }= & 2.68 \\ & \widehat{\alpha }= & 11.72 \\ & \widehat{n}= & -4.00 \end{align} }[/math]

Once the parameters are obtained, one can now determine the reliability for these units at any time [math]\displaystyle{ t }[/math] and stress [math]\displaystyle{ x(t) }[/math] from:

[math]\displaystyle{ R\left( t,x\left( t \right) \right)={{e}^{-{{\left[ \mathop{}_{0}^{t}{{\left[ \tfrac{x(u)}{a} \right]}^{n}}du \right]}^{\beta }}}} }[/math]

or at a fixed stress level [math]\displaystyle{ x(t)=2V }[/math] and [math]\displaystyle{ t=300 }[/math] ,

[math]\displaystyle{ R\left( t=300,x(t)=2 \right)={{e}^{-{{\left[ \mathop{}_{0}^{t}{{\left[ \tfrac{x(u)}{a} \right]}^{n}}du \right]}^{\beta }}}}=97.5% }[/math]

The mean time to failure (MTTF) at any stress [math]\displaystyle{ x(t) }[/math] can be determined by:

[math]\displaystyle{ MTTF\left( x\left( t \right) \right)=\mathop{}_{0}^{\infty }t\left[ \left\{ \beta {{\left[ \frac{x\left( t \right)}{a} \right]}^{n}}{{\left[ \mathop{}_{0}^{t}{{\left[ \frac{x\left( u \right)}{a} \right]}^{n}}du \right]}^{\beta -1}} \right\}{{e}^{-{{\left[ \mathop{}_{0}^{t}{{\left[ \tfrac{x(u)}{a} \right]}^{n}}du \right]}^{\beta }}}} \right]dt }[/math]

or at a fixed stress level [math]\displaystyle{ x\left( t \right)=2V }[/math] ,

[math]\displaystyle{ MTTF\left( x\left( t \right) \right)=1046.3hrs }[/math]

The same result can be calculated using ALTA PRO as shown next.

[math]\displaystyle{ }[/math]

Any other metric of interest (e.g. failure rate, conditional reliability etc.) can also be determined using the basic definitions given in Appendix A and calculated automatically with ALTA PRO.

Cumulative Damage General Log-Linear Relationship

This section presents a generalized formulation of the cumulative damage model where multiple stress types are used in the analysis and where the stresses can be any function of time.

Cumulative Damage General Log-Linear - Exponential

Given [math]\displaystyle{ n }[/math] time-varying stresses [math]\displaystyle{ \underline{X}=({{X}_{1}}(t),{{X}_{2}}(t)...{{X}_{n}}(t)) }[/math] , the life-stress relationship is:

[math]\displaystyle{ \frac{1}{m\left( t,\overset{\_}{\mathop{x}}\, \right)}=s(t,\overset{\_}{\mathop{x}}\,)={{e}^{-{{a}_{0}}-\underset{j=1}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{a}_{j}}{{x}_{j}}(t)}} }[/math]

where [math]\displaystyle{ {{\alpha }_{0}} }[/math] and [math]\displaystyle{ {{\alpha }_{j}} }[/math] are model parameters. This relationship can be further modified through the use of transformations and can be reduced to the relationships discussed previously (power, Arrhenius and exponential), if so desired. The exponential reliability function of the unit under multiple stresses is given by:

[math]\displaystyle{ R(t,\overset{\_}{\mathop{x}}\,)={{e}^{-I(t,\overset{\_}{\mathop{x}}\,)}} }[/math]

where:

[math]\displaystyle{ I(t,\overset{\_}{\mathop{x}}\,)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,\frac{du}{{{e}^{^{^{{{\alpha }_{0}}+\overset{n}{\mathop{\underset{j=1}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}(t)}}}}} }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,\overset{\_}{\mathop{x}}\,)=s(t,\overset{\_}{\mathop{x}}\,){{e}^{-I(t,\overset{\_}{\mathop{x}}\,)}} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [s({{T}_{i}},{{\overset{\_}{\mathop{x}}\,}_{i}})]-\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\left( I({{T}_{i}},{{\overset{\_}{\mathop{x}}\,}_{i}}) \right) \\ & & -\overset{S}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }\left( I(T_{i}^{\prime },\overset{\_}{\mathop{x}}\,_{i}^{\prime }) \right)+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }(T_{Li}^{\prime \prime },\overset{\_}{\mathop{x}}\,_{i}^{\prime \prime })= & {{e}^{-I(T_{Li}^{\prime \prime },\overset{\_}{\mathop{x}}\,_{i}^{\prime \prime })}} \\ & R_{Ri}^{\prime \prime }(T_{Ri}^{\prime \prime },\overset{\_}{\mathop{x}}\,_{i}^{\prime \prime })= & {{e}^{-I(T_{Ri}^{\prime \prime },\overset{\_}{\mathop{x}}\,_{i}^{\prime \prime })}} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact time-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• .. is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• .. is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage General Log-Linear - Weibull

Given [math]\displaystyle{ n }[/math] time-varying stresses [math]\displaystyle{ \underline{X}=({{X}_{1}}(t),{{X}_{2}}(t)...{{X}_{n}}(t)) }[/math] , the life-stress relationship is given by:

[math]\displaystyle{ \frac{1}{\eta \left( t,\overset{\_}{\mathop{x}}\, \right)}=s(t,\overset{\_}{\mathop{x}}\,)={{e}^{^{^{-{{a}_{0}}-\overset{n}{\mathop{\underset{j=1}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}(t)}}}} }[/math]

where [math]\displaystyle{ {{\alpha }_{j}} }[/math] are model parameters.
The Weibull reliability function of the unit under multiple stresses is given by:

[math]\displaystyle{ R(t,\overset{\_}{\mathop{x}}\,)={{e}^{-{{\left( I(t,\overset{\_}{\mathop{x}}\,) \right)}^{\beta }}}} }[/math]

where:

[math]\displaystyle{ I(t,\overset{\_}{\mathop{x}}\,)=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,\frac{du}{{{e}^{^{{{a}_{0}}+\underset{j=1}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}(u)}}}} }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,\overset{\_}{\mathop{x}}\,)=\beta s(t,\overset{\_}{\mathop{x}}\,){{\left( I(t,\overset{\_}{\mathop{x}}\,) \right)}^{\beta -1}}{{e}^{-{{\left( I(t,\overset{\_}{\mathop{x}}\,) \right)}^{\beta }}}} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [\beta s({{T}_{i}},{{\overset{\_}{\mathop{x}}\,}_{i}}){{\left( I({{T}_{i}},{{\overset{\_}{\mathop{x}}\,}_{i}}) \right)}^{\beta -1}}]-\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}{{\left( I({{T}_{i}},{{\overset{\_}{\mathop{x}}\,}_{i}}) \right)}^{\beta }} \\ & & -\overset{S}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }{{\left( I(T_{i}^{\prime },\overset{\_}{\mathop{x}}\,_{i}^{\prime }) \right)}^{\beta }}+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [R_{Li}^{\prime \prime }-R_{Ri}^{\prime \prime }] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & R_{Li}^{\prime \prime }(T_{Li}^{\prime \prime },\bar{x}_{i}^{\prime \prime })= & {{e}^{-{{\left( I(T_{Li}^{\prime \prime },\bar{x}_{i}^{\prime \prime }) \right)}^{\beta }}}} \\ & R_{Ri}^{\prime \prime }(T_{Ri}^{\prime \prime },\bar{x}_{i}^{\prime \prime })= & {{e}^{-{{\left( I(T_{Ri}^{\prime \prime },\bar{x}_{i}^{\prime \prime }) \right)}^{\beta }}}} \end{align} }[/math]

and:
[math]\displaystyle{ {{i}^{th}} }[/math]
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact time-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

Cumulative Damage General Log-Linear - Lognormal

Given [math]\displaystyle{ n }[/math] time-varying stresses [math]\displaystyle{ \underline{X}=({{X}_{1}}(t),{{X}_{2}}(t)...{{X}_{n}}(t)) }[/math] , the life-stress relationship is given by:

[math]\displaystyle{ \frac{1}{\breve{T}(t,\bar{x})}=s(t,\overset{\_}{\mathop{x}}\,)={{e}^{^{^{-{{a}_{0}}-\overset{n}{\mathop{\underset{j=1}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}(t)}}}} }[/math]

where [math]\displaystyle{ {{\alpha }_{j}} }[/math] are model parameters.
The lognormal reliability function of the unit under multiple stresses is given by:

[math]\displaystyle{ R(t,\bar{x})=1-\Phi (z(t,\bar{x})) }[/math]

where:

[math]\displaystyle{ z(t,\bar{x})=\frac{\ln I(t,\bar{x})}{\sigma _{T}^{\prime }} }[/math]

and:

[math]\displaystyle{ I(t,\bar{x})=\underset{0}{\mathop{\overset{t}{\mathop{\mathop{}_{}^{}}}\,}}\,\frac{du}{{{e}^{^{{{\alpha }_{0}}+\underset{j=1}{\mathop{\overset{n}{\mathop{\mathop{}_{}^{}}}\,}}\,{{\alpha }_{j}}{{x}_{j}}(u)}}}} }[/math]

Therefore, the [math]\displaystyle{ pdf }[/math] is:

[math]\displaystyle{ f(t,\bar{x})=\frac{s(t,\bar{x})\varphi (z(t,\bar{x}))}{\sigma _{T}^{\prime }I(t,\bar{x})} }[/math]

Parameter estimation can be accomplished via maximum likelihood estimation methods, and confidence intervals can be approximated using the Fisher matrix approach. Once the parameters are determined, all other characteristics of interest can be obtained utilizing the statistical properties definitions (e.g. mean life, failure rate, etc.) presented in previous chapters. The log-likelihood equation is as follows:

[math]\displaystyle{ \begin{align} & \ln (L)= & \Lambda =\overset{Fe}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,{{N}_{i}}\ln [\frac{s({{T}_{i}},{{{\bar{x}}}_{i}})\varphi (z({{T}_{i}},{{{\bar{x}}}_{i}}))}{\sigma _{T}^{\prime }I({{T}_{i}},{{{\bar{x}}}_{i}})}] \\ & & \overset{S}{\mathop{\underset{i=1}{\mathop{+\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime }\ln \left( 1-\Phi (z(T_{i}^{\prime },\bar{x}_{i}^{\prime })) \right)+\overset{FI}{\mathop{\underset{i=1}{\mathop{\underset{}{\overset{}{\mathop \sum }}\,}}\,}}\,N_{i}^{\prime \prime }\ln [\Phi (z_{Ri}^{\prime \prime })-\Phi (z_{Li}^{\prime \prime })] \end{align} }[/math]

where:

[math]\displaystyle{ \begin{align} & z_{Ri}^{\prime \prime }= & \frac{\ln I(T_{Ri}^{\prime \prime },\bar{x}_{i}^{\prime \prime })}{\sigma _{T}^{\prime }} \\ & z_{Li}^{\prime \prime }= & \frac{\ln I(T_{Li}^{\prime \prime },\bar{x}_{i}^{\prime \prime })}{\sigma _{T}^{\prime }} \end{align} }[/math]

and:
• [math]\displaystyle{ {{F}_{e}} }[/math] is the number of groups of exact time-to-failure data points.
• [math]\displaystyle{ {{N}_{i}} }[/math] is the number of times-to-failure in the [math]\displaystyle{ {{i}^{th}} }[/math] time-to-failure data group.
• [math]\displaystyle{ {{T}_{i}} }[/math] is the exact failure time of the [math]\displaystyle{ {{i}^{th}} }[/math] group.
• [math]\displaystyle{ S }[/math] is the number of groups of suspension data points.
• [math]\displaystyle{ N_{i}^{\prime } }[/math] is the number of suspensions in the [math]\displaystyle{ {{i}^{th}} }[/math] group of suspension data points.
• [math]\displaystyle{ T_{i}^{\prime } }[/math] is the running time of the [math]\displaystyle{ {{i}^{th}} }[/math] suspension data group.
• [math]\displaystyle{ FI }[/math] is the number of interval data groups.
• [math]\displaystyle{ N_{i}^{\prime \prime } }[/math] is the number of intervals in the [math]\displaystyle{ {{i}^{th}} }[/math] group of data intervals.
• [math]\displaystyle{ T_{Li}^{\prime \prime } }[/math] is the beginning of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.
• [math]\displaystyle{ T_{Ri}^{\prime \prime } }[/math] is the ending of the [math]\displaystyle{ {{i}^{th}} }[/math] interval.

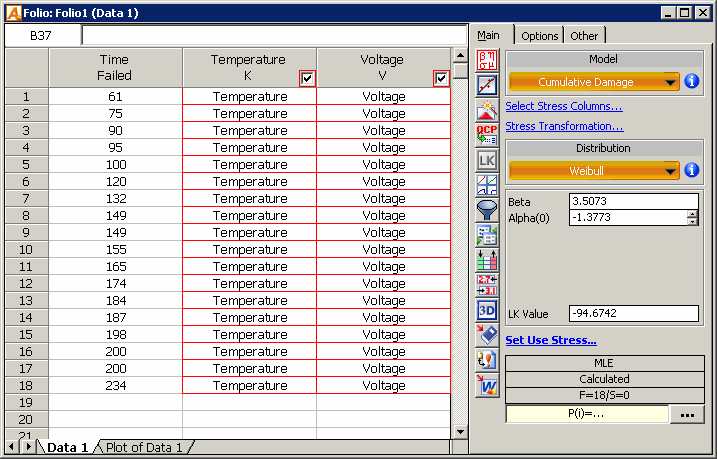
Example

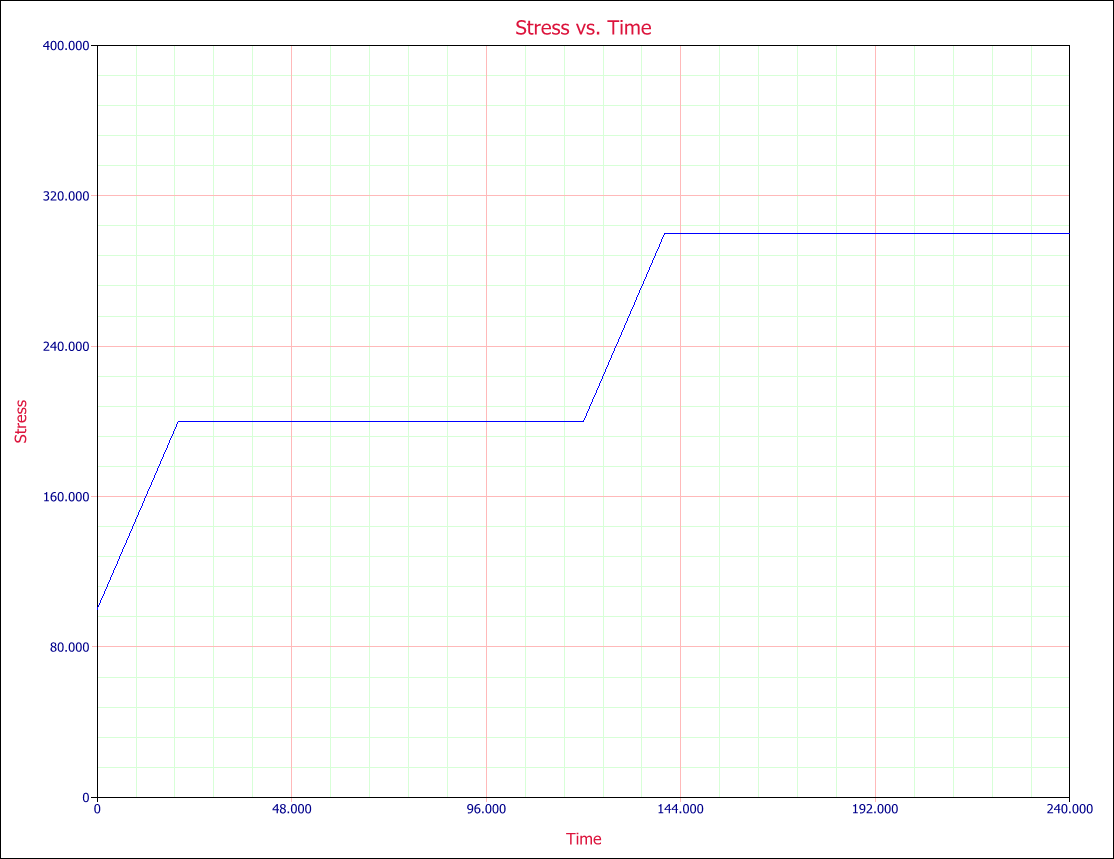
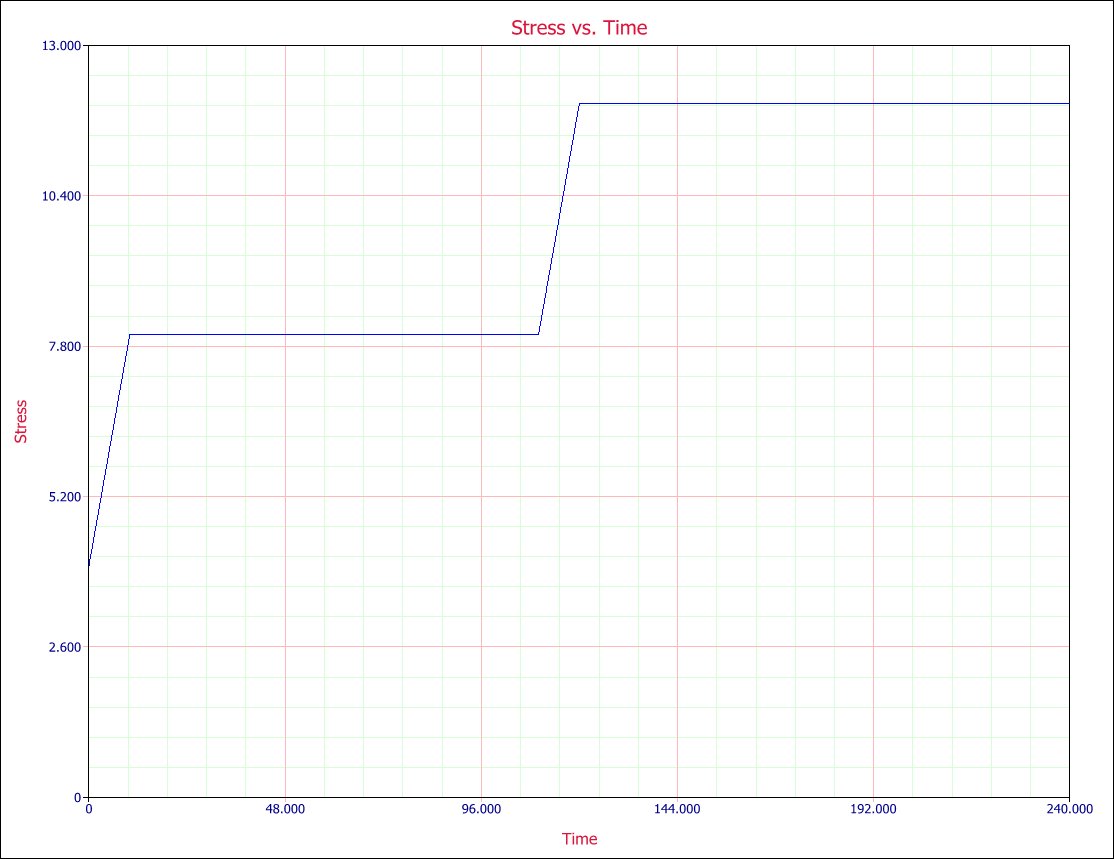
A sample of 18 units of an electronic component was subjected to temperature and voltage stresses. The temperature was initially set 100K and was then continuously increased to 200K over a period of 20 hours. The temperature was again increased at 120 hours to 300K over a 20 hours period as shown in Fig. 3. The voltage was initially set 4V and was then increased continuously to 8V over a period of 10 hours. The voltage was again increased at 110 hours to 12V over a 10 hours period as shown in Fig. 4.

Fig. 3: Temperature profile.

Fig. 4: Voltage profile.

[math]\displaystyle{ }[/math]

The failure times, as entered in ALTA PRO, are shown in the next figure.

The stresses are transformed using an Arrhenius life-stress relationship for temperature, a Power Law life-stress reliationship for voltage and the Weibull distribution as the underlying distribution.

[math]\displaystyle{ }[/math]

The estimated model parameters are shown next.

[math]\displaystyle{ \begin{align} & \widehat{\beta }= & 3.5073 \\ & \widehat{{{\alpha }_{0}}}= & -1.3773 \\ & \widehat{{{\alpha }_{1}}}= & 450.46 \\ & \widehat{{{\alpha }_{2}}}= & 1.98 \end{align} }[/math]

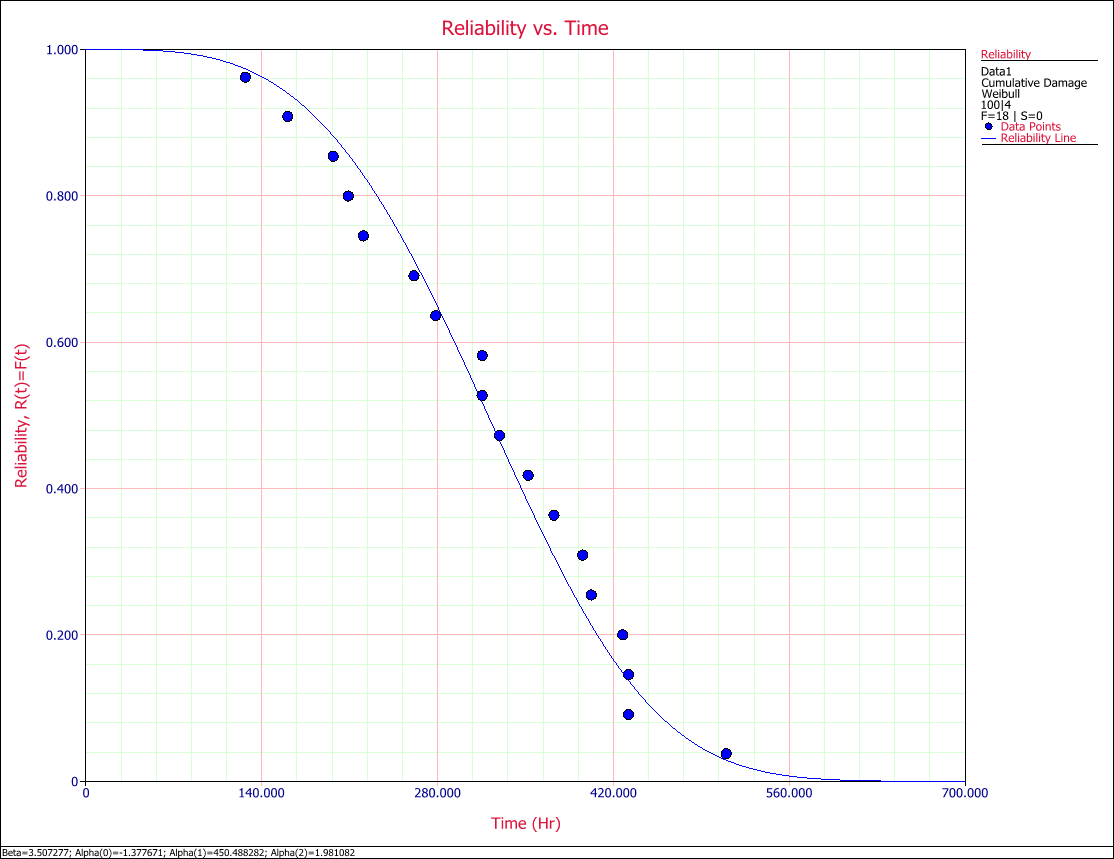
The use level (temperature = 100K, voltage = 4V) reliability plot is shown in the next figure.

Fig. 5: Reliability plot at normal use conditions (100K and 4V).

Confidence Intervals

Using the same methodology as in previous sections, approximate confidence intervals can be derived and applied to all results of interest using the Fisher Matrix approach discussed in Appendix A. ALTA PRO utilizes such intervals on all results. The formulas for such intervals are beyond the scope of this reference and are thus omitted. Interested readers can contact ReliaSoft for internal document ALTA-CBCD, detailing these derivations.